
Рабочие тетради №2-9 / Рабочая тетрадь _5
.doc|
5
43 Момент распределения k-го порядка – средняя величина отклонений k-й степени от некоторой постоянной величины А:
Если А – произвольное число, то моменты условные.
Если А = 0, то моменты начальные;
m0
= 1; m1
– средняя арифметическая (
Если А
=
Нормированные моменты:
μ0=1; μ1=0; μ2=1.
Для центральных моментов можно вывести зависимости от начальных моментов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П
44 Нормированный момент третьего порядка является показателем асимметрии распределения As:
Рис. 5.2. Асимметрия распределения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С
45
Если
В качестве показателя асимметрии применяется и коэффициент асимметрии Пирсона (As):
Если As=
0, (т.е.
Если As < 0, то имеет место левосторонняя асимметрия. Если As > 0,то имеет место правосторонняя асимметрия. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
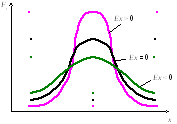
46 Нормированный момент четвертого порядка характеризует крутизну (заостренность) графика распределения:
Показатель эксцесса рассчитывается:
Если Ex = 0, то распределение симметрично; Ex > 0, то распределение островершинное; Ex < 0, то распределение плосковершинное (рис. 5.3).
Рис. 5.3. Эксцесс распределения Степень существенности эксцесса характеризуется средней квадратической ошибкой:
Пример 5.4. ДОМАШНЕЕ ЗАДАНИЕ. По данным примера 5.1 рассчитать показатели асимметрии и эксцесса. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
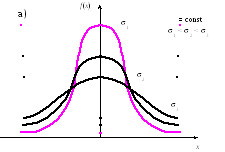
47 Распределение непрерывной случайной величины x называют нормальным, если соответствующая ей плотность распределения выражается формулой
или
где x – значение изучаемого признака; s2 – дисперсия значений изучаемого признака; s – среднее квадратическое отклонение изучаемого признака; π = 3,1415926; е = 2,7182;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48
Рис. 5.4. Кривые нормального распределения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49 Порядок расчета теоретических частот кривой нормального распределения:
где N – объем совокупности; hi – длина интервала. Для
вариационного ряда с равными интервалами:
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
П
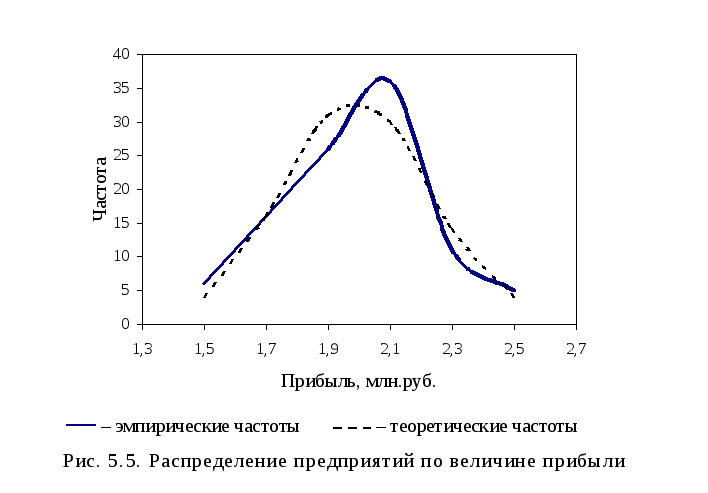
50 Рассчитать теоретические частоты ряда распределения на основании данных о прибыли предприятий города, представленных в табл. 5.6. Таблица 5.6
Анализируемый вариационный ряд имеет равные интервалы, следовательно:
Последовательно
умножив const
на величину j(t)
для каждого варианта, получим
теоретические частоты
Сравним на графике
эмпирические fi
и теоретические
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
51 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
52 При проверке статистических гипотез часто используют следующие характеристики: уровень значимости a и число степеней свободы v. Уровень значимости a – вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. В статистических исследованиях пользуются тремя уровнями значимости: a = 0,10; a = 0,05; a = 0,01. Число степеней свободы v определяется как число групп в ряду распределения m минус число связей k: v = m – k. В случае выравнивания по кривой нормального распределения имеется три связи:
При выравнивании по кривой нормального распределения v = m – 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К
53
(5.43)
где m – число групп в эмпирическом распределении; fi , wi – наблюдаемые частота и частость признака в i-й группе;
Для оценки существенности расчетное значение c2расч сравнивается с табличным c2т. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К
54
Если c ≤ 3, то расхождения между теоретическими и эмпирическими частотами случайны.
Критерий Колмогорова λ :
где D
– максимальная (по модулю) разность
между накопленными частотами
эмпирического
и теоретического распределений ( Рассчитав значение λ, по таблице P(λ) определяют вероятность, с которой можно утверждать, что отклонения эмпирических частот от теоретических случайны. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
П
55 Таблица 5.7
Критерий Пирсона:
c2расч
При α=0,05 и v = 3 табличное значение критерия c2т = 7,81. c2расч ≤ c2т.
Критерий Романовского:
Критерий Колмогорова:
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

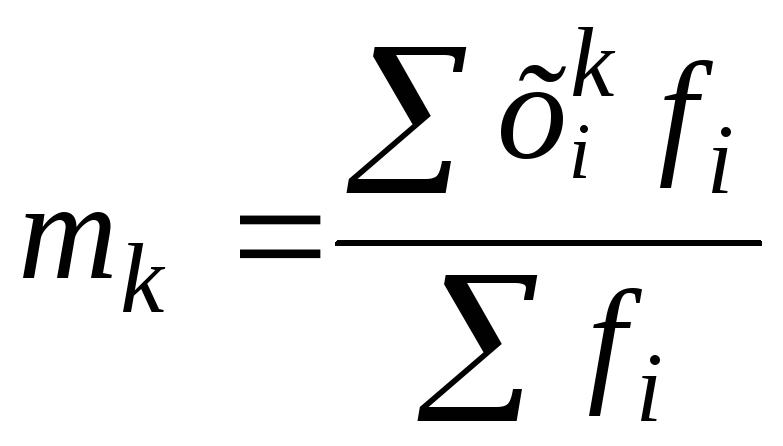 (5.32)
(5.32)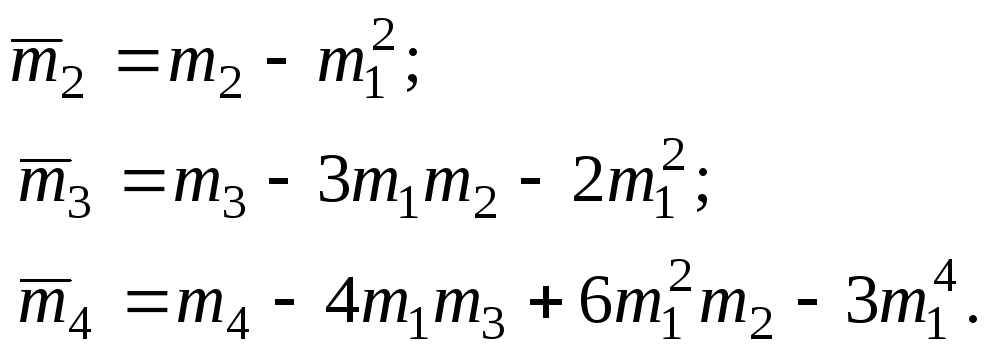

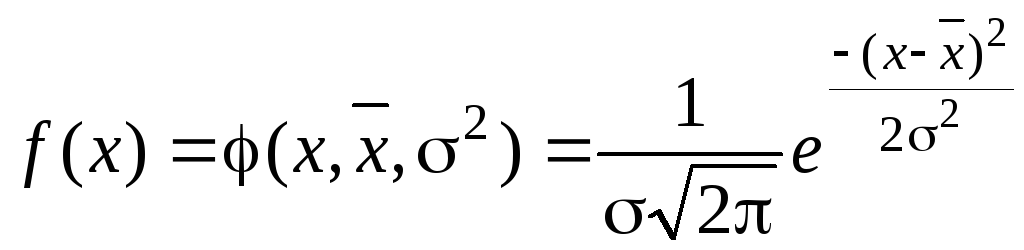 ,
,

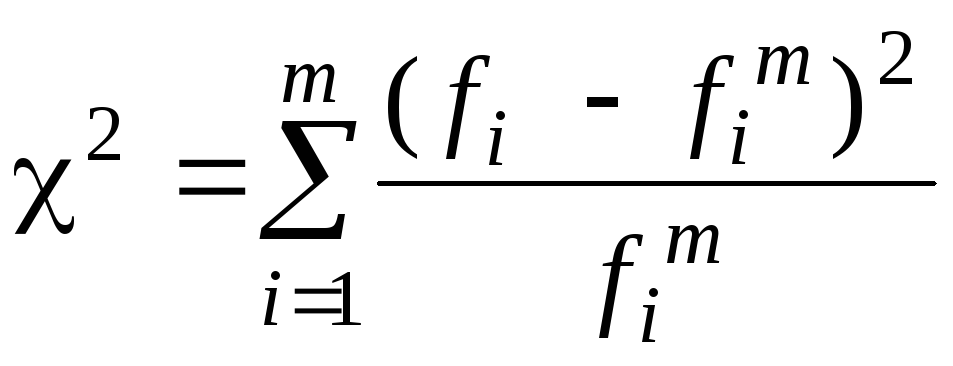 или
или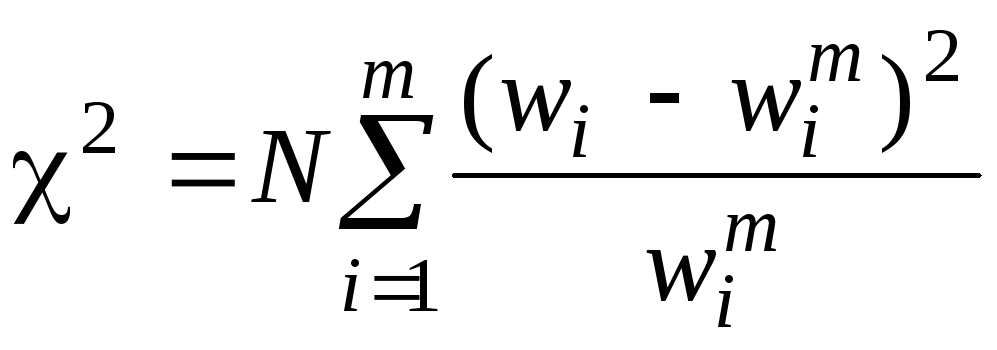 ,
,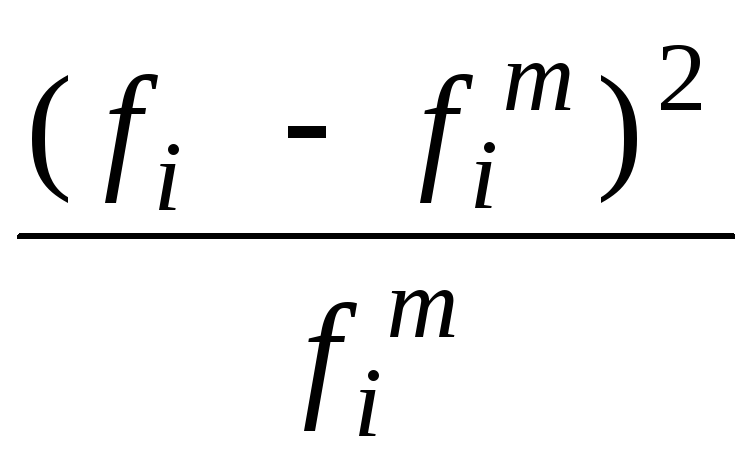
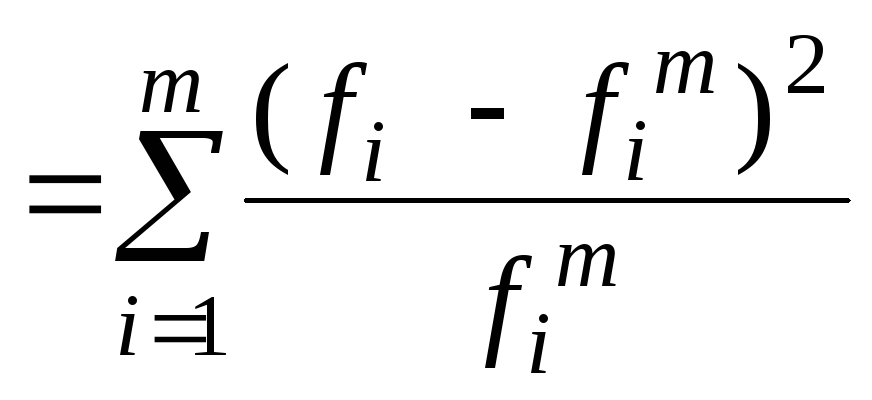 =
3,90.
=
3,90.