Характеристика предприятий района (данные условные)
-
Номер предприятия
Объем
реализации, тыс.руб.
Объем реализации на
1 работника, тыс.руб./чел.
Рентабельность, %
Доля рабочих
в общей
численности
работников, %
Среднемесячная зарплата
на 1 работника, руб./чел.
2
362728
1242
26,3
74,3
5420
3
257206
989
27,3
71,4
4456
4
257721
1227
21,7
72,3
4681
5
224238
901
20,6
73,9
3574
Решение: 1) Среднее значение реализованной продукции на одного работника определю по формуле средней гармонической взвешенной тыс.Руб/чел
2) Среднее значение производительности труда определю по формуле средней арифметической простой
3)Среднее значение заработной платы определю по формуле средней арифметической взвешенной руб.
3. Структурные средние величины
3.1. По результатам экзамена в группе определить моду, медиану:
1) аналитическим методом
2) графическим методом.
|
Оценка |
Количество оценок |
|
5 |
7 |
|
4 |
5 |
|
3 |
11 |
|
2 |
4 |
Решение: 1) аналитический метод
|
x |
f |
s | |
|
2 |
4 |
4 | |
|
3 |
11 |
15 | |
|
4 |
5 |
20 | |
|
5 |
7 |
27 | |
|
|
27 |
| |
Мо=3,
т.к.
=
11
Ме=
3, т.к.
2) графический метод
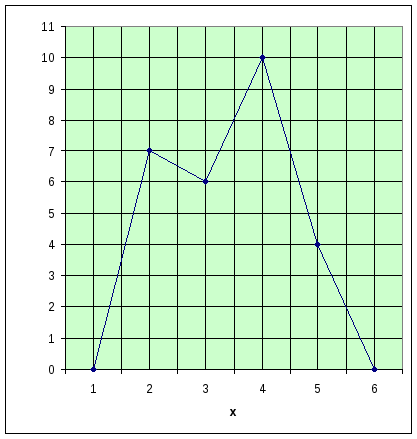
3.2. На основе имеющихся данных о распределении предприятий города по объему выпуска продукции определить моду, медиану:
1) аналитическим методом
2) графическим методом.
-
Группа предприятий по объему выпуска, млн.руб.
Количество предприятий
До 40
8
40 – 50
10
50 – 60
18
60 – 70
24
70 – 80
22
80 – 90
23
90 – 100
17
Более 100
8
Решение: 1) аналитический метод
|
x |
f |
s | |
|
До 40 |
8 |
8 | |
|
40 – 50 |
10 |
18 | |
|
50 – 60 |
18 |
36 | |
|
мод60 – 70 |
24 |
60 | |
|
мед70 – 80 |
22 |
82>65 | |
|
80 – 90 |
23 |
105 | |
|
90 – 100 |
17 |
122 | |
|
Более 100 |
8 |
130 | |
|
|
130 |
| |
=
60+10*(24-18)/((24-18)+(24-22))=
=60+10*6/8=67,5
,
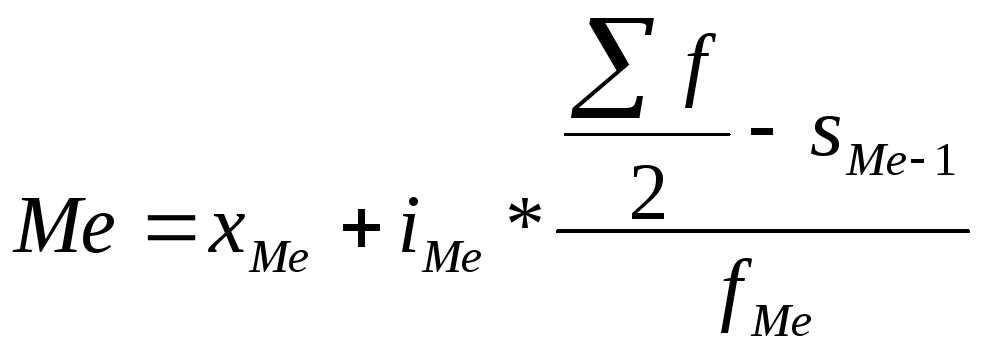т.к. 83>65 (130/2), то
Ме = 70 +10*(65-60)/22=72,27
2) графический метод
. Показатели вариации
4.1. Супермаркет имеет данные о покупках, совершаемых покупателями за определенный период. Рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности исследуемой совокупности.
|
Сумма покупки, тыс.руб. |
Количество покупок |
|
До 100 |
24 |
|
100 – 200 |
28 |
|
200 – 300 |
40 |
|
300 – 400 |
32 |
|
400 – 500 |
26 |
|
500 – 600 |
19 |
Решение: промежуточные данные удобно представить в таблице
Таблица 4.1.1