§ 2. Оптимальное закрепление потребителей за поставщиками и клиентуры за автохозяйствами

Одним из основных вопросов планирования перевозок является закрепление потребителей за поставщиками. Постановка этой задачи состоит в следующем.

Имеется ряд поставщиков и потребителей однородной продукции. Заданы расстояния между всеми поставщиками и потребителями, объем поставок и потребления каждым из них. Необходимо найти такой план закрепления потребителей за поставщиками, который обеспечивает минимальный объем транс портной работы в тонно-километрах или наименьшее среднее расстояние перевозки груза.

Аналогичны постановка и задачи по закреплению клиентуры за автохозяйствами: имеются автохозяйства, начальные пункты погрузки и конечные пункты разгрузки. Заданы расстояния между автохозяйствами и всеми указанными пунктами, известно количество подвижного состава, которое необходимо подавать на каждый маршрут или клиенту. Строится план за крепления маршрутов и клиентуры за автохозяйствами, при котором общий нулевой пробег всех автомобилей будет минимальным.

К этому же типу задач относится оптимальное закрепление автобусных маршрутов за несколькими автобусными парками.

Оптимальный вариант решения всех указанных задач можно получить, используя методы решения транспортной задачи линейного программирования, один из которых дан в § 1 главы XIII.

Однако в практике работы автотранспортных организаций при решении этих задач могут возникать различные дополнительные требования, которые необходимо учитывать в процессе планирования. Ограничения, вытекающие из этих требований, следует внести в матрицу для того, чтобы они были учтены.

Одним из таких условий может стать невозможность поставок некоторым потребителям продукции определенных поставщиков (или закрепления той или иной клиентуры за некоторыми автохозяйствами) по дорожным условиям из-за договорных отношений ввиду специальных требований к продукции или к подвижному составу.

Такое ограничение можно учесть при решении, если в матрице в клетку, которая лежит на пересечении строки соответствующего потребителя (клиента) и столбца соответствующего поставщика (автохозяйства), вместо фактического расстояния между этими пунктами записать расстояние, значительно боль шее любого другого расстояния в матрице. Если при этом потребность данного потребителя (клиента) не превышает наличия груза (подвижного состава) у остальных поставщиков (автохозяйств), то указанная клетка в оптимальном решении останется незагруженной, и тем самым будет выдержано заданное ограничение.

В некоторых случаях необходимо решать задачи, когда наличие груза (автомобилей) и спрос не являются сбалансированными.

Если общий объем наличия превышает спрос всех потребителей, то в матрицу дополнительно вводится так называемый фиктивный потребитель, для которого отводится отдельная строка. Его спрос принимается равным превышению общего объема наличия груза (автомобилей) над суммарным объемом спроса всех реальных потребителей. Вместо расстояний в клетках этой строки матрицы записывают любое произвольно вы бранное число, но одинаковое по всем столбцам.

Если общий объем наличия меньше суммарного спроса всех потребителей, то в матрицу вводят столбец фиктивного поставщика (автохозяйства), размер поставок которого принимают равным превышению суммарного спроса над общим объемом поставок и в этом столбце также вместо расстояния по всем клеткам записывают любое одинаковое число.

Введем некоторые указанные выше факторы в решение задачи, данной в § 1 главы XIII (см. табл. 13).

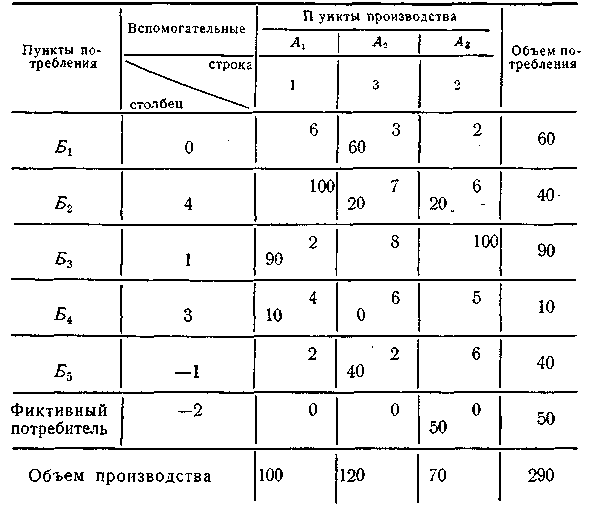
Так, устанавливаем, что потребителю Б2 нельзя доставлять груз от поставщика А1, а потребителю Б3 — от поставщика А3. В связи с этим в матрице (табл. 15) в соответствующих клетках вместо фактических расстояний поставим большое число—100.

Кроме того, объем производства в пункте А1 примем за 100, А2—120 и А3—70, т. е. общий объем производства превышает спрос на 50. В связи с этим в матрицу вводим строку «фиктивный потребитель» с объемом потребления 50, а во всех клетках этой строки вместо расстояния записываем любое одинаковое число, в данном случае 0.

Решают эту матрицу распределительным методом. Полученный оптимальный вариант представлен в табл. 15.

Таблица 15 Матрица с учетом заданных условий перевозок

Известны способы учета при решении транспортных задач и некоторых других факторов: ограниченных пропускных способностей дорог, верхних и нижних границ объемов производства, взаимозаменяемости грузов и т. д.

С помощью указанных выше методов могут быть найдены оптимальные решения задачи размещения автохозяйств на территории города, области, а также распределения различного подвижного состава по автохозяйствам.