20.1. Определение шара

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не больше данного от некоторой точки, называемой центром шара. Данное расстояние называется радиусом шара.

Граница шара называется шаровой поверхностью или сферой. Таким образом, точками сферы являются все точки шара, удаленные от центра шара на расстояние, равное радиусу.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.

Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полуокружности вокруг ее диаметра.

Задачи

1. На поверхности шара даны три точки. Прямолинейные расстояния между ними 6, 8 и 10. Радиус шара 13. Найти расстояние от центра шара до плоскости, проходящей через эти три точки.

2. Диаметр шара 25. На его поверхности даны точка и окружность, все точки которой удалены (по прямой) от на 15. Найти радиус этой окружности.

3. Радиус шара равен 7. На его поверхности даны две окружности, имеющие общую хорду длиной 2. Найти радиусы окружностей, зная, что их плоскости перпендикулярны.

21. Сечение тел вращения

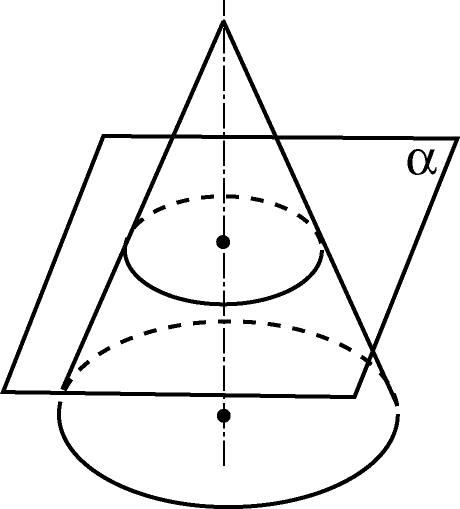
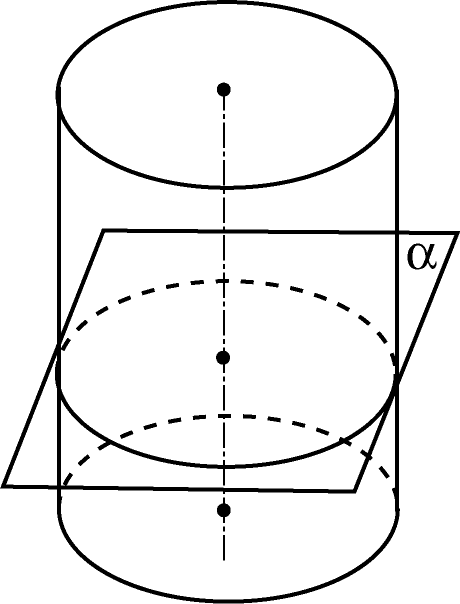
Сечением цилиндра или конуса плоскостью, параллельной плоскости основания, является окружность равная (для цилиндра) или подобная (для конуса) основанию.

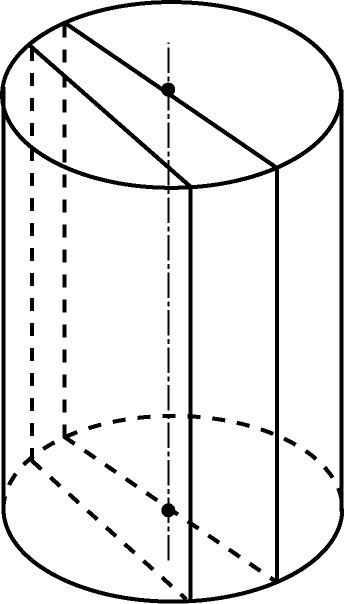
Сечением цилиндра плоскостями, параллельными образующим являются прямоугольники. Сечением плоскостями, проходящими через вершину конуса, являются треугольники.

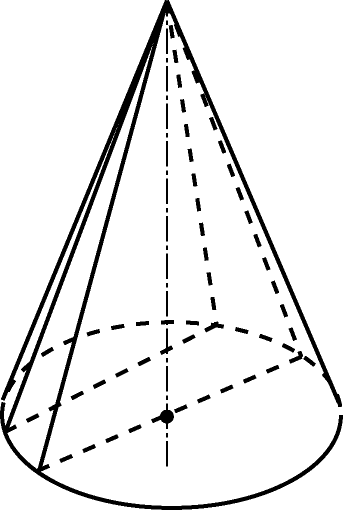
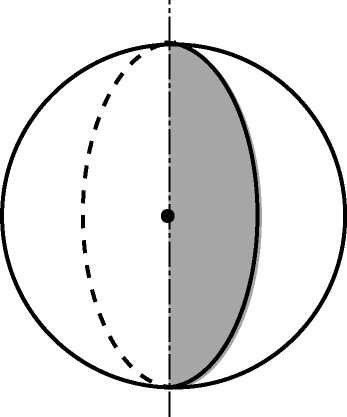
Осевым называется сечение, проходящее через ось тела вращения. Осевое сечение шара (сферы) также называется диаметральным.

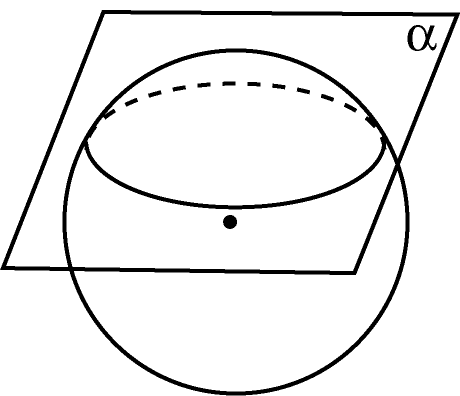
Всякое сечение шара плоскостью есть круг. Цент этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

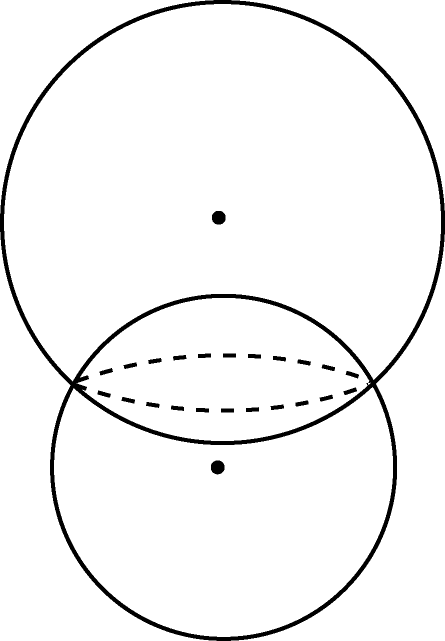
Линия пересечения двух сфер есть окружность. Других точек пересечения они не имеют.

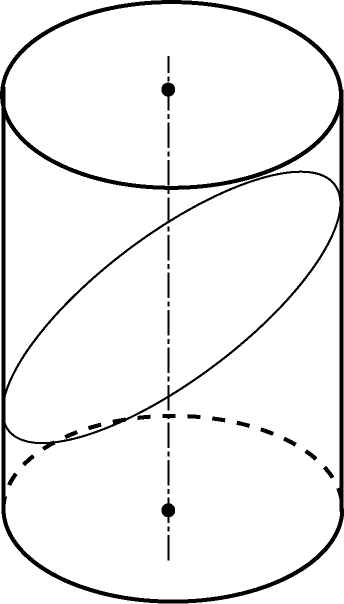
Сечением цилиндра или конуса плоскостью, не параллельной плоскости основания и не проходящей через вершину конуса является либо эллипс (если плоскость не пересекает основание), либо парабола и прямая (если плоскость пересекает основание).

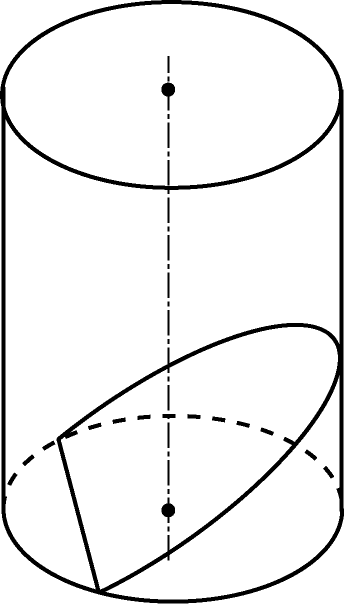
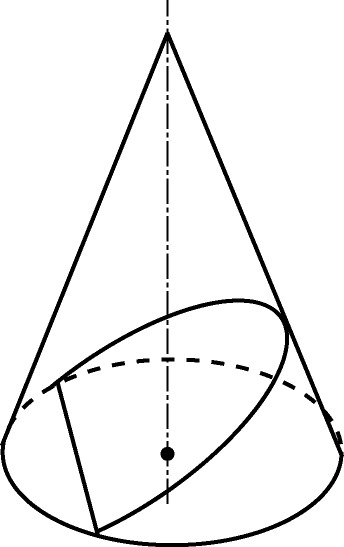
Задачи

1. Высота цилиндра 6, радиус основания 5. Найти площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 от нее.

2. В равностороннем конусе (в осевом сечении правильный треугольник) радиус основания 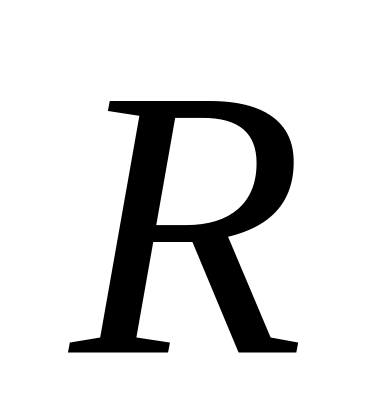. Найти площадь сечения, проведенного через две образующие, угол между которыми равен .

3. Высота конуса 20, радиус его основания 25. Найти площадь сечения, проведенного через вершину, если расстояние от него до центра основания конуса равно 12.

4. Радиус основания конуса , образующая наклонена к плоскости основания под углом . Через вершину конуса проведена плоскость под углом 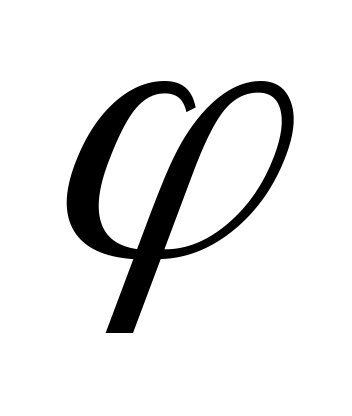к его высоте. Найти площадь получившегося сечения.

5. Через середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга.

6. Радиус шара . Через конец радиуса проведена плоскость под углом 60^о к нему. Найти площадь получившегося сечения.

7. Два равных шара радиуса расположены так, что центр одного из них лежит на поверхности другого. Найдите длину линии, по которой пересекаются их поверхности.

8. Радиусы шаров равны 25 и 29, а расстояние между их центрами 39. найти длину линии, по которой пересекаются их поверхности.