Тела вращения

18. Цилиндр

18.1. Определение и свойства цилиндра

Цилиндром (точнее круговым цилиндром) называется тело, которое состоит из двух кругов, лежащих в параллельных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей, – образующими.

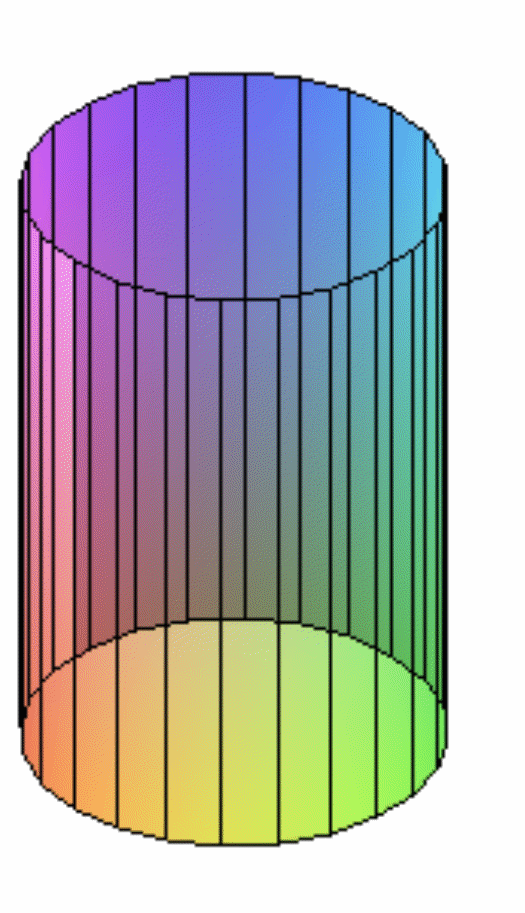
Цилиндр обладает следующими свойствами, следующими из того факта, что основания цилиндра совмещаются параллельным переносом:

1. Основания цилиндра равны.

2. Образующие цилиндра параллельны и равны.

Цилиндр называется прямым если его образующие перпендикулярны плоскостям оснований. В дальнейшем будем рассматривать в основном прямые цилиндры, поэтому, если не оговорено обратное, под цилиндром будем понимать прямой цилиндр.

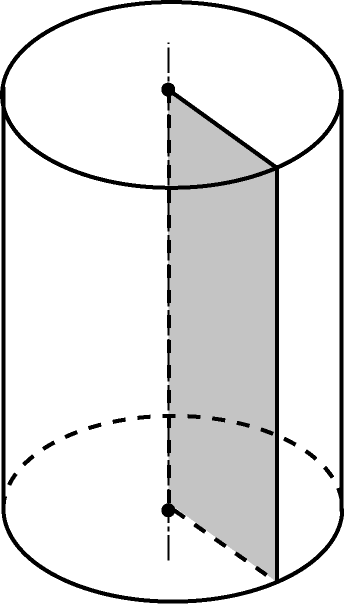
Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Для прямого цилиндра высота равна образующим. Осью цилиндра назевается прямая, проходящая через центры оснований.

Цилиндр является телом вращения, так как может быть получен вращением прямоугольника вокруг своей оси.

Задачи

1. Высота цилиндра 6, радиус основания 5. Концы отрезка 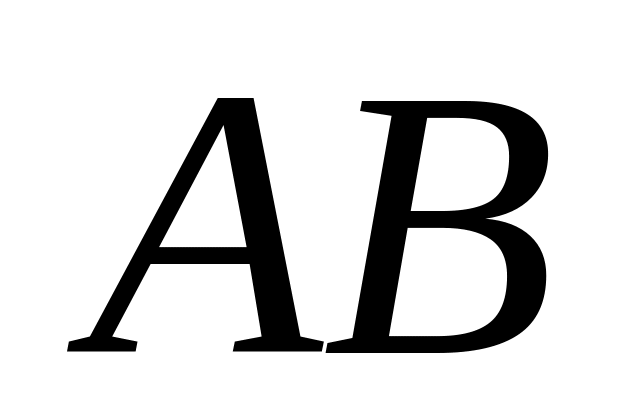, равного 10, лежат на окружностях обоих оснований. Найти кратчайшее расстояние от этого отрезка до оси цилиндра.

2. В равностороннем цилиндре (диаметр равен высоте цилиндра) точка окружности верхнего основания соединена с точкой окружности нижнего основания. Угол между радиусами, проведенным в эти точки, равен 60^о. Найти угол между проведенным отрезком и осью цилиндра.

19. Конус

19.1. Определение конуса

Конусом (точнее круговым конусом) называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости основания, – вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершины конуса с точками окружности основания, называются образующими конуса.

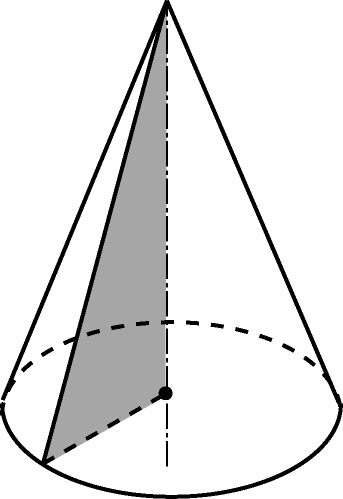
Выстой конуса называется перпендикуляр, опущенный из вершины конуса на плоскость основания. Если основание высоты совпадает с центром окружности основания, конус называется прямым. Далее под конусом будем обычно понимать прямой конус.

Осью прямого кругового конуса называется прямая, содержащая его высоту. Такой конус может быть получен вращением прямоугольного треугольника вокруг одного из катетов.

19.2. Усеченный конус

Плоскость, параллельная основанию конуса, отсекает от него подобный конус. Оставшаяся часть называется усеченным конусом.

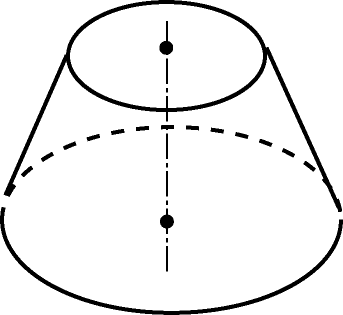
Задачи

1. Две образующие конуса, опирающиеся на концы диаметра основания, составляют между собой угол 60^о. Радиус конуса равняется 3. Найти образующую конуса и его высоту.

2. Через середину высоты конуса проведена прямая, параллельная образующей . Найти длину отрезка прямой, заключенной внутри конуса.

3. Образующая конуса равна 13, высота 12. Конус пересечен прямой, параллельной основанию; расстояние от нее до основания равно 6, а до высоты – 2. Найти отрезок прямой, заключенный внутри конуса.

4. Радиусы оснований усеченного конуса равны 3 и 6, высота – 4. Найти образующую.

20. Шар