17.5. Объем пирамиды

Теорема 17.1. Две треугольные пирамиды с равными площадями оснований и равными высотами равновелики.

Пусть – треугольная пирамида. Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой. Эта призма будет состоять из исходной пирамиды и двух равновеликих ей треугольных пирамид и .

Докажем, что эти две пирамиды равновелики исходной. Действительно, у второй и третей пирамид равные основания – и и общая высота, проведенная из вершины . У первой и третей пирамид тоже равны основания – и и общая высота, проведенная из вершины .

Таким образом, все три пирамиды имеют равный объем, значит

.

Рассмотрим теперь произвольную пирамиду. Разобьем ее на треугольных пирамид с общей вершиной и треугольниками в основании, составляющими основание исходной пирамиды. Все треугольные пирамиды будут иметь одинаковую высоту, равную высоте исходной пирамиды. Объем исходной пирамиды равен сумме объемов треугольных пирамид:

.

Таким образом, объем произвольной пирамиды равняется одной трети произведения площади ее основания на высоту.

17.6. Объем усеченной пирамиды

Найдем объем усеченной пирамиды с площадями оснований и и высотой .

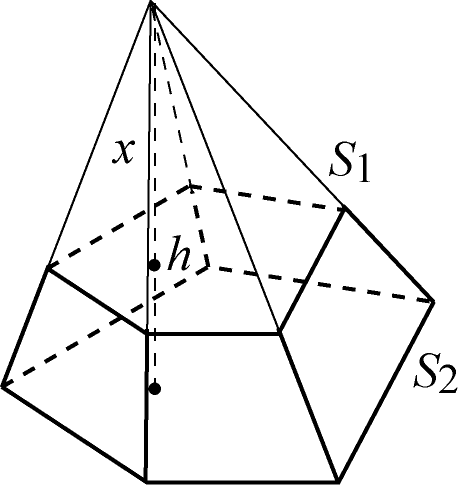
Пусть – высота отсеченной пирамиды. Тогда – высота пирамиды, из которой получилась данная усеченная. Поскольку эта пирамида подобна отсеченной, то их основания относятся как квадрат коэффициента подобия, который равен :

.

Откуда

Объем усеченной пирамиды равен разности объемов полной и отсеченной пирамид:

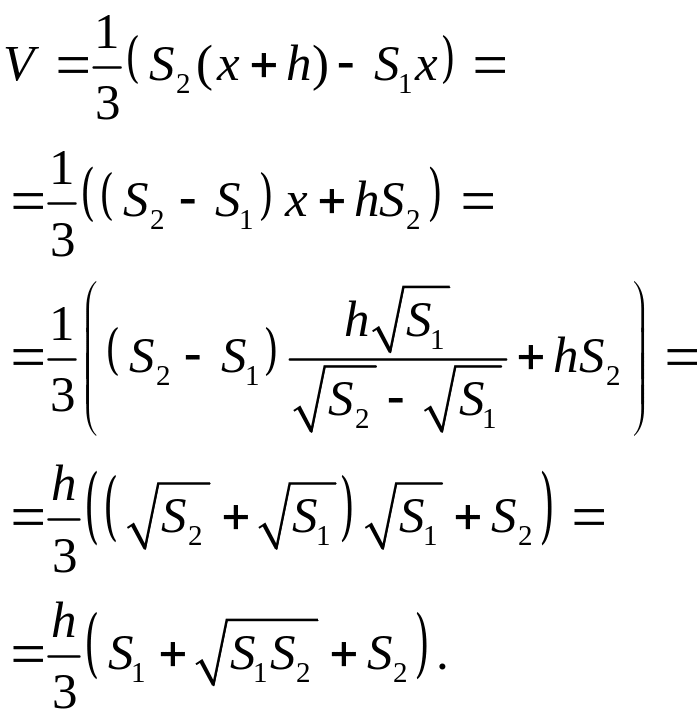
Задачи

1. Основание прямого параллелепипеда – ромб, площадь которого кв. ед. Площади диагональных сечений кв. ед. и кв. ед. Найти объем параллелепипеда.

2. В параллелепипеде длины трех ребер, исходящих из одной вершины, равны , , . Ребра и взаимно перпендикулярны, а ребро образует с каждым из них угол . Найти объем параллелепипеда.

3. Грани параллелепипеда – равные ромбы со стороной и острым углом 60^о. Найти объем параллелепипеда.

4. Высота пирамиды . На каком расстоянии от вершины находится сечение, параллельное основанию и делящее ее объем пополам.

5. По стороне основания и боковому ребру найдите объем правильной призмы: а) треугольной; б) четырехугольной; в) шестиугольной.

6. В правильной шестиугольной призме площадь наибольшего диагонального сечения 4 кв. ед., а расстояние между двумя противоположными боковыми гранями 2. Найти объем призмы.

7. Чему равен объем прямой четырехугольной призмы, если ее высота , диагонали наклонены к плоскости основания под углами и , а острый угол между диагоналями оснований равен .

8. По стороне основания и боковому ребру найдите объем правильной пирамиды: а) треугольной; б) четырехугольной; в) шестиугольной.

9. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое равно . Найти объем пирамиды.

10. Основание пирамиды – равнобедренный треугольник со сторонами 6, 6, 8. Все боковые ребра равны 9. Найти объем пирамиды.

11. В правильной усеченной четырехугольной пирамиде стороны нижнего и верхнего оснований равны и , а двугранный угол при ребре нижнего основания равен . Найти объем пирамиды.