
- •Многогранники
- •13. Призма
- •13.1. Определение и свойства призмы
- •13.2. Прямая призма
- •13.3. Параллелепипед
- •14. Пирамида
- •14.1. Определение и свойства пирамиды
- •14. 2. Усеченная пирамида
- •14.3. Правильная пирамида
- •15. Правильные многогранники
- •16. Сечение многогранников
- •16.1. Виды сечений многогранников
- •16.2. Построение сечения плоскостью, проходящей через заданные прямую и точку
- •17. Объемы многогранников
- •17.1. Понятие объема
- •17.2. Объем прямоугольного параллелепипеда
- •17.3. Объем наклонного параллелепипеда
- •17.4. Объем призмы
- •17.5. Объем пирамиды
- •17.6. Объем усеченной пирамиды
- •Тела вращения
- •18. Цилиндр
- •18.1. Определение и свойства цилиндра
- •19. Конус
- •19.1. Определение конуса
- •19.2. Усеченный конус
- •20.1. Определение шара
- •21. Сечение тел вращения
- •22. Вписанные и описанные тела
- •22.1. Касательная плоскость
- •22.2. Определения вписанных и описанных тел
- •22.3. Свойства вписанных тел
- •23. Объемы и площади поверхности тел вращения
- •23.1. Объем и площадь боковой поверхности цилиндра
- •23.2. Объем и площадь боковой поверхности конуса
- •23.3. Объем шара и площадь сферы
- •23.4. Объем шарового сектора и шарового сегмента
17. Объемы многогранников
17.1. Понятие объема
Объемом тела называется положительная величина, обладающая следующими свойствами:
Равные тела имеют равные объемы
Если тело разбить на части, то объем этого тела равен сумме объемов его частей
Объем куба, ребро которого равно единице длины, равен единицы
Два тела называются равновеликими, если
они имеют равные объемы. Если два тела
подобны с коэффициентом подобия
![]() ,
то их объемы относятся с коэффициентом
,
то их объемы относятся с коэффициентом
![]() :
:
![]() .
.
17.2. Объем прямоугольного параллелепипеда
Найдем объем прямоугольного параллелепипеда
с линейными размерами
,
,
.
Пусть эти два параллелепипеда имеют
общее основание
![]() и высоты
и высоты
![]() и
и
![]() (
(![]() ).,
и пусть
).,
и пусть
![]() и
и
![]() – объемы этих тел.
– объемы этих тел.
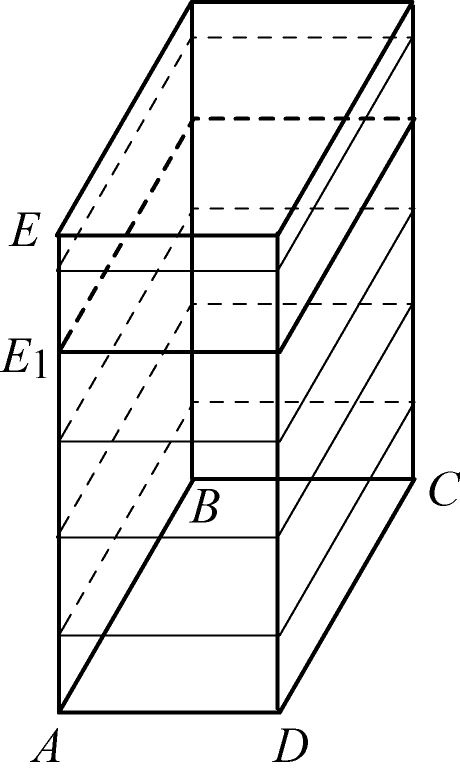
Разобьем ребро
на
![]() равных частей, каждая из которых равна
равных частей, каждая из которых равна
![]() и пусть
и пусть
![]() – чисто точек деления, которые лежат
на ребре
.
Тогда
– чисто точек деления, которые лежат
на ребре
.
Тогда

Проведем через точки деления плоскости,
параллельные основанию параллелепипеда.
Они разобьют первый параллелепипед на
равных частей, объемом
![]() .
Тогда объем второго параллелепипеда
будет заключен в следующих пределах:
.
Тогда объем второго параллелепипеда
будет заключен в следующих пределах:

Таким образом, объемы двух прямоугольных параллелепипедов с равными основаниями относятся как их высоты.
Рассмотрим теперь куб с единичным
ребром, объем которого по определению
равен 1, и три прямоугольных параллелепипеда
с измерениями
![]() ;
;
![]() и
и
![]() и объемами
,
и объемами
,
![]() и
,
соответственно. По доказанному выше
и
,
соответственно. По доказанному выше
![]() ,
,
![]() ,
,
![]() .
Перемножая эти три равенства, получаем
.
Перемножая эти три равенства, получаем
![]() .
.
Таким образом, объем прямоугольного параллелепипеда равен произведению его трех линейных размеров.
17.3. Объем наклонного параллелепипеда
Найдем объем наклонного параллелепипеда .
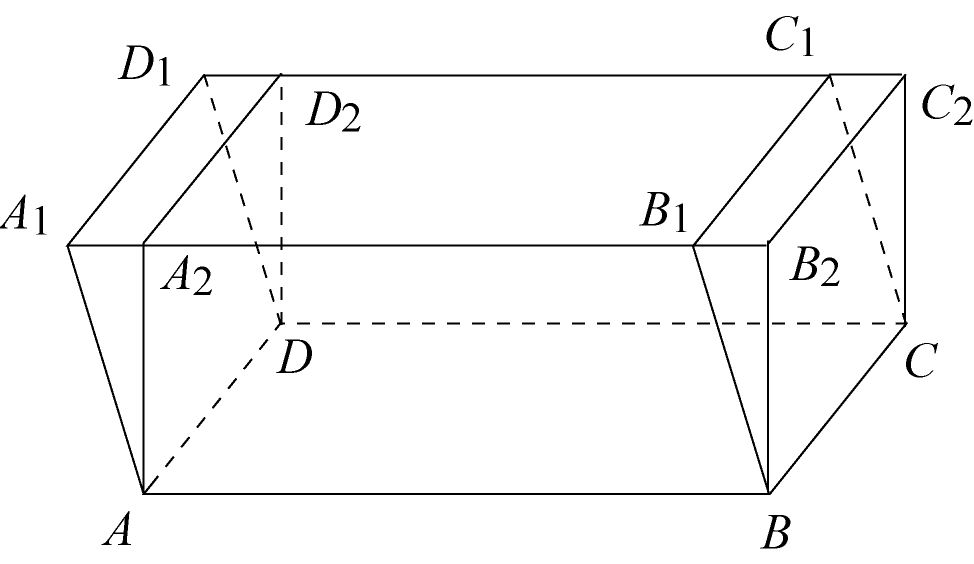
Проведем через ребро
![]() плоскость, перпендикулярную основанию
,
и дополним наклонный параллелепипед
треугольной призмой
плоскость, перпендикулярную основанию
,
и дополним наклонный параллелепипед
треугольной призмой
![]() .
Теперь отсечем плоскостью, проходящей
через ребро
перпендикулярно основанию призмы
,
от полученного тела треугольную призму
.
Теперь отсечем плоскостью, проходящей
через ребро
перпендикулярно основанию призмы
,
от полученного тела треугольную призму
![]() .
Получим новый параллелепипед
.
Получим новый параллелепипед
![]() ,
объем которого равен объему исходного
параллелепипеда
,
т.к. призмы
и
равны. При описанном преобразовании
сохраняются также площадь его основания
и высота. При этом плоскости двух граней
сохраняются, а плоскости двух других
становятся перпендикулярны основаниям.
,
объем которого равен объему исходного
параллелепипеда
,
т.к. призмы
и
равны. При описанном преобразовании
сохраняются также площадь его основания
и высота. При этом плоскости двух граней
сохраняются, а плоскости двух других
становятся перпендикулярны основаниям.
Применяя еще раз подобное преобразование
к наклонным граням, получим прямой
параллелепипед. Полученный прямой
параллелепипед аналогичным преобразованием
превратим в прямоугольный, дополнив
его сначала призмой
![]() ,
а затем удалив призму
,
а затем удалив призму
![]() .
Это преобразование также сохраняет
объем параллелепипеда, площадь основания
и высоту.
.
Это преобразование также сохраняет
объем параллелепипеда, площадь основания
и высоту.
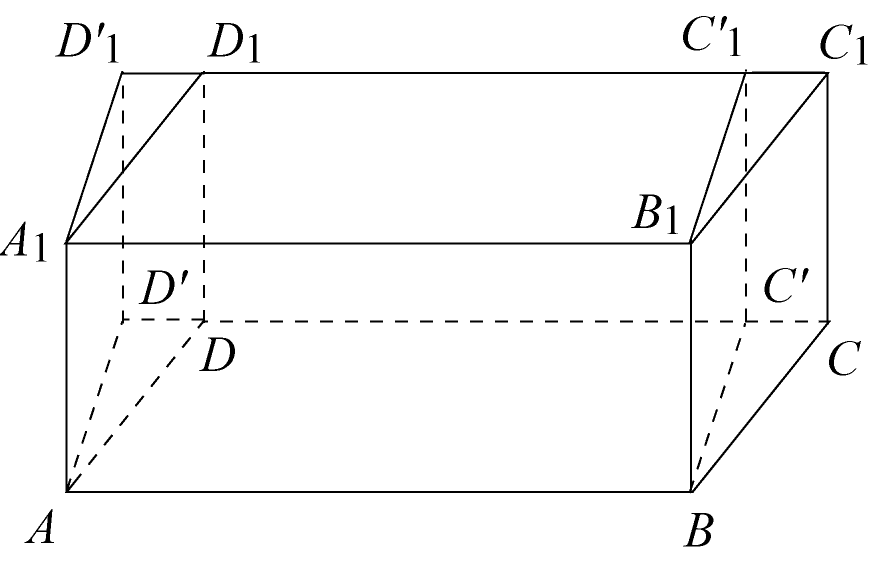
Объем прямоугольного параллелепипеда равен произведению всех трех его измерений, или что то же самое, произведению площади основания на высоту. Поскольку все вышеописанные преобразования сохраняли объем параллелепипеда, площадь основания и высоту, значит объем наклонного параллелепипеда также равен произведению площади основания на высоту.
17.4. Объем призмы
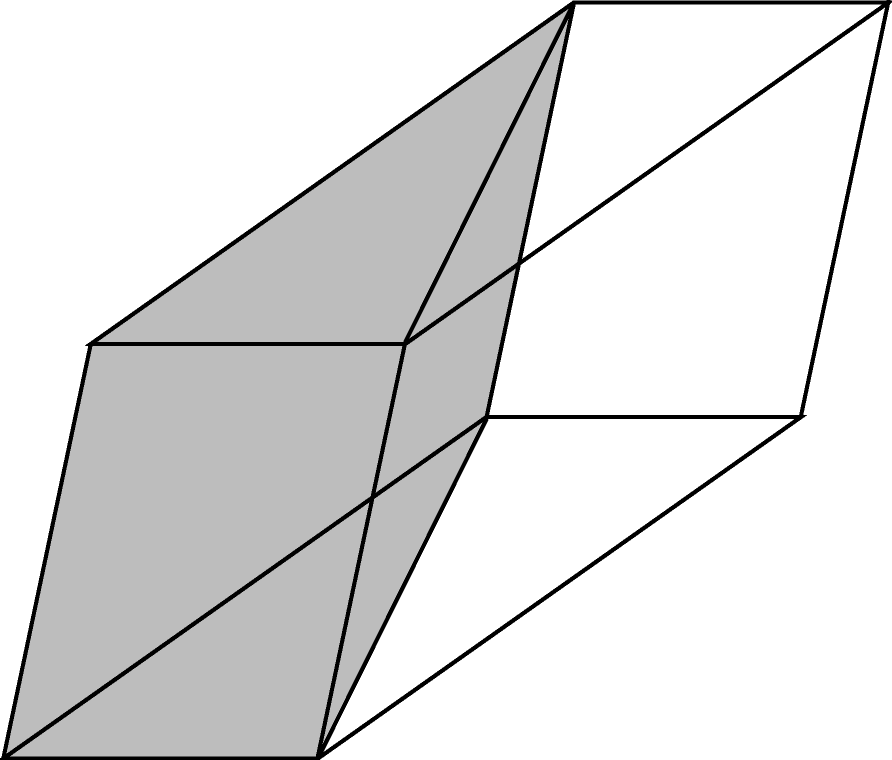
Рассмотрим сначала треугольную призму. Дополним ее до параллелепипеда такой же призмой. Объем получившегося параллелепипеда будет вдвое больше объема призмы и равен произведению площади основания на высоту. У призмы и параллелепипеда высоты одинаковые, а площадь основания параллелепипеда вдвое больше площади основания призмы. Следовательно, объем исходной призмы равен произведению площади основания на высоту.
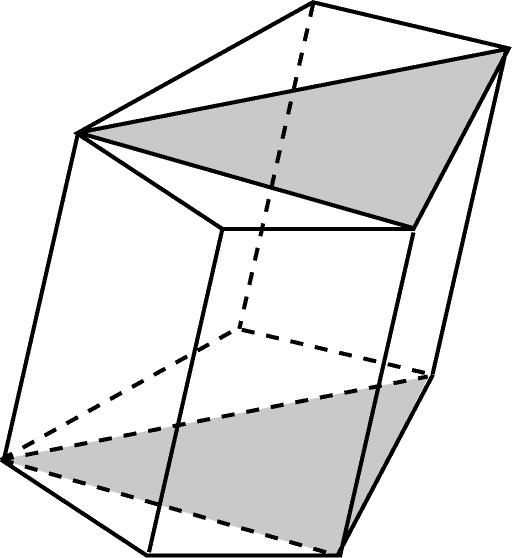
Рассмотрим теперь произвольную призму. Разобьем ее основания на треугольников, а исходную призму – на треугольные призмы с боковыми ребрами, параллельными ребрам исходной призмы. При этом объем произвольной призмы будет равен сумме объемов треугольных призм, площадь ее основания будет равна сумме площадей треугольника, а высоты у всех призм будут одинаковы. Таким образом, объем произвольной призмы равен:
![]() .
.
Таким образом, объем любой призмы равен произведению площади ее основания на высоту.
