14. Пирамида

14.1. Определение и свойства пирамиды

Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, – вершины пирамиды, и всех отрезков, соединяющих вершину пирамиды с точками основания.

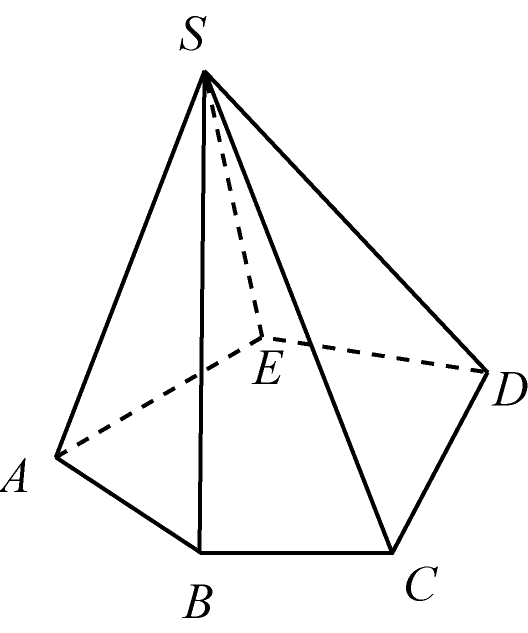
Отрезки, соединяющие вершину пирамиды с вершинами оснований, называются ребрами пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Грани, не являющиеся основанием пирамиды, называются боковыми гранями. Все боковые грани пирамиды – треугольники. Пирамида называется n-угольной, если в ее основании лежит n-угольник. Треугольную пирамиду также называют тетраэдром.

Теорема 14.1. Если в пирамиде все высоты боковых граней, проведенные из вершины пирамиды равны, то

1. все боковые грани наклонены к плоскости основания под равными углами;

2. вершина пирамиды проектируется в центр окружности, вписанной в основание.

Доказательство. Рассмотрим пирамиду в которой высоты боковых граней равны . Проведем высоту пирамиды и рассмотрим треугольники , , . Это прямоугольные треугольники с общим катетом и равными гипотенузами , значит эти треугольники равны. Отсюда , т.е. равны углы наклона боковых граней к плоскости основания. Из равенства треугольников также следует равенство сторон , т.е. точка является центром вписанной в основание пирамиды окружности.

Теорема 14.2. Если в пирамиде все боковые ребра равны, то

1. все боковые ребра наклонены к плоскости основания под равными углами;

2. вершина пирамиды проектируется в центр окружности, описанной около основания.

Верны также обратные утверждения.

14. 2. Усеченная пирамида

Проведем плоскость, параллельную основанию пирамиды и пересекающую эту пирамиды. Эта плоскость разделит пирамиду на два многогранника, один из которых представляет собой пирамиду меньшего размера и называется отсеченной пирамидой, второй – усеченной пирамидой.

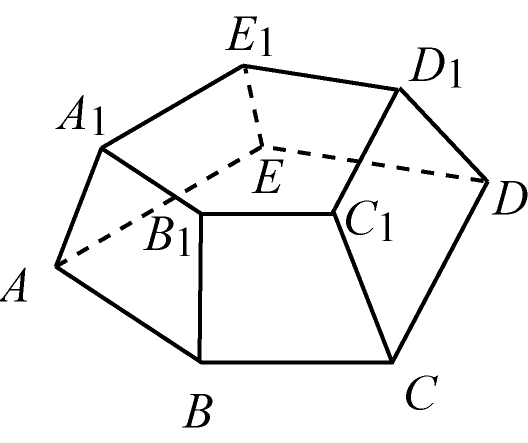
Грани усеченной пирамиды, лежащие в параллельных плоскостях, называются основаниями, остальные – боковыми гранями. Основания усеченной пирамиды являются подобными многоугольниками, а боковые грани представляют собой трапеции.

Теорема 14.3. Плоскость, параллельная основанию пирамиды, отсекает подобную пирамиду (без доказательства).

14.3. Правильная пирамида

Пирамида называется правильной, если ее основанием является правильной многоугольник и основание высоты совпадает с центром этого многоугольника. Очевидно, что у правильной пирамиды все боковые ребра равны, следовательно все ее боковые грани – равнобедренные треугольники.

Осью правильной пирамиды называется прямая, содержащая ее высоту. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой ( ). Все апофемы равны и являются биссектрисами и медианами боковых граней.

Теорема 14.4. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.

Доказательство. Боковые грани правильной пирамиды есть равные треугольники, основания которых являются сторонами многоугольников в основаниях пирамиды, а апофемы являются высотами боковых граней пирамиды. Тогда по определению площадь боковой поверхности:

,

где – периметр основания правильной n-угольной пирамиды.

Усеченная пирамида, которая получается из правильной, также называется правильной. Боковыми гранями правильной усеченной пирамиды являются равнобокие трапеции, их высоты называются апофемами.

Задачи

1. Доказать, что боковые ребра правильной треугольной пирамиды перпендикулярны противоположным ребрам основания.

2. Доказать, что основание перпендикуляра, опущенного из вершины основания правильной треугольной пирамиды на боковую грань , лежит на высоте этой боковой грани.

3. Основание пирамиды – равнобедренный треугольник с основанием 12 и боковой стороной 10. Боковые грани образуют с основанием двугранные углы 45^о. Найти высоту пирамиды (ответ: 3).

4. Основание пирамиды – ромб с диагоналями 6 и 8, высота пирамиды проходит через точку пересечения диагоналей ромба и равна 1. Найти боковую поверхность пирамиды (ответ: 26).

5. Основание пирамиды – квадрат, ее высота проходит через одну из вершин основания. Найти боковую поверхность пирамиды, если сторона основания равна 20, а высота 21 (ответ: 10).

6. В треугольной пирамиде все ребра равны. Найти угол между скрещивающимися медианами двух соседних граней.

7. Найти боковую поверхность усеченной правильной пирамиды.

8. Высота пирамиды равна 16. Площадь основания равна 512. Найти высоту усеченной пирамиды, меньшее основание которой равно 50.

9. По стороне основания и высоте найти полную поверхность правильно пирамиды а) треугольной, б) четырехугольной, в) шестиугольной.

10. В правильной четырехугольной пирамиде плоский угол при вершине равен . Найти двугранный угол при основании пирамиды

11. В правильной усеченной четырехугольной пирамиде стороны оснований равны 8 и 2, высота равна 4. Найти полную поверхность пирамиды.

12. Доказать, что боковая поверхность правильной усеченной пирамиды равна произведению полсуммы периметров оснований на апофему.