Многогранники

Основным объектом изучения стереометрии являются пространственные тела. Тело представляет собой часть пространства, ограниченную некоторой поверхностью.

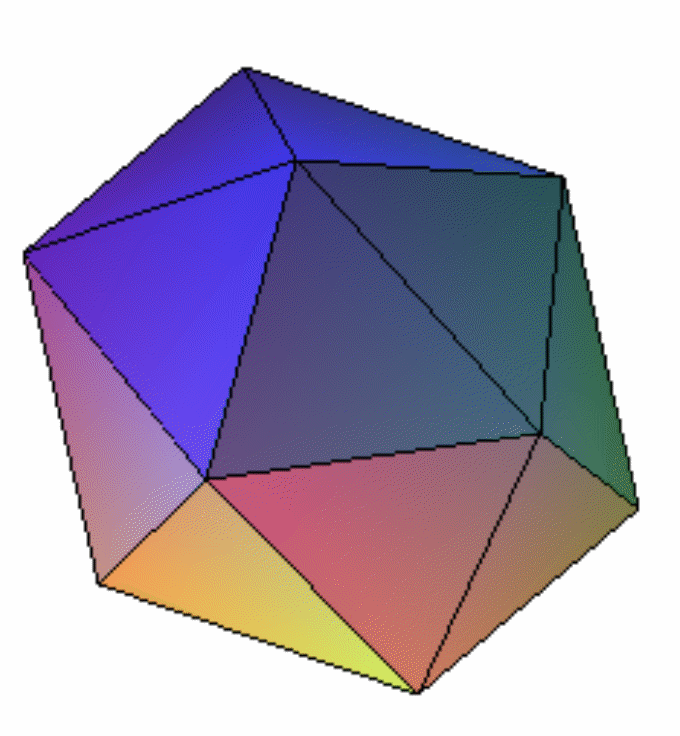
Многогранником называется тело, поверхность которого состоит из конечного числа плоских многоугольников. Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называется ребрами многогранника, а вершины – вершинами многогранника.

Например, куб состоит из шести квадратов, являющихся его гранями. Он содержит 12 ребер (стороны квадратов) и 8 вершин (вершины квадратов).

Простейшими многогранниками являются призмы и пирамиды, изучением которых и займемся далее.

13. Призма

13.1. Определение и свойства призмы

Призмой называется многогранник, состоящий из двух плоских многоугольников, лежащих в параллельных плоскостях совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины многоугольников, – боковыми ребрами призмы.

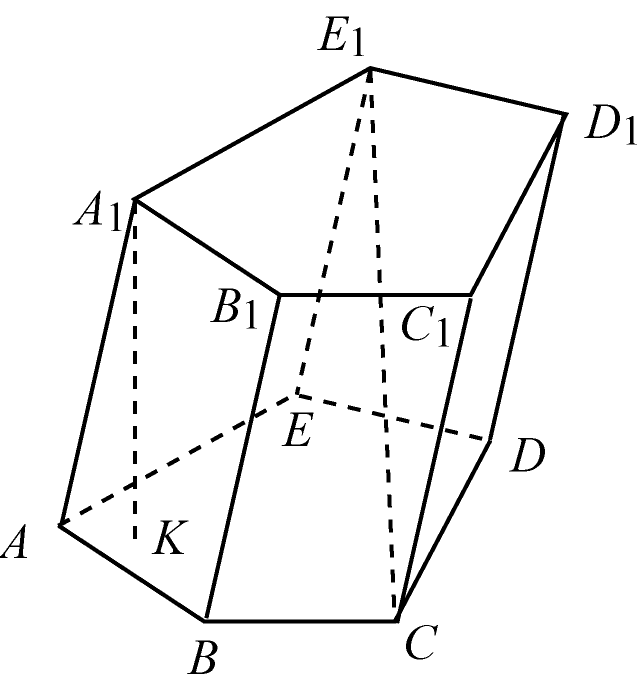
Высотой призмы называется расстояние между плоскостями ее оснований ( ). Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы ( ). Призма называется n-угольной, если в ее основании лежит n-угольник.

Любая призма обладает следующими свойствами, следующими из того факта, что основания призмы совмещаются параллельным переносом:

1. Основания призмы равны.

2. Боковые ребра призмы параллельны и равны.

Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность призмы состоит из параллелограммов (это следует из свойств призмы). Площадью боковой поверхности призмы называется сумма площадей боковых граней.

13.2. Прямая призма

Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной.

Гранями прямой призмы являются прямоугольники. Высота прямой призмы равна ее боковым граням.

Полной поверхностью призмы называется сумма площади боковой поверхности и площадей оснований.

Правильной призмой называется прямая призма с правильным многоугольником в основании.

Теорема 13.1. Площадь боковой поверхности прямой призмы равна произведению периметра на высоту призмы (или, что то же самое, на боковое ребро).

Доказательство. Боковые грани прямой призмы есть прямоугольники, основания которых являются сторонами многоугольников в основаниях призмы, а высоты являются боковыми ребрами призмы. Тогда по определению площадь боковой поверхности:

,

где – периметр основания прямой призмы.

13.3. Параллелепипед

Если в основаниях призмы лежат параллелограммы, то она называется параллелепипедом. У параллелепипеда все грани – параллелограммы. При этом противолежащие грани параллелепипеда параллельны и равны.

Теорема 13.2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

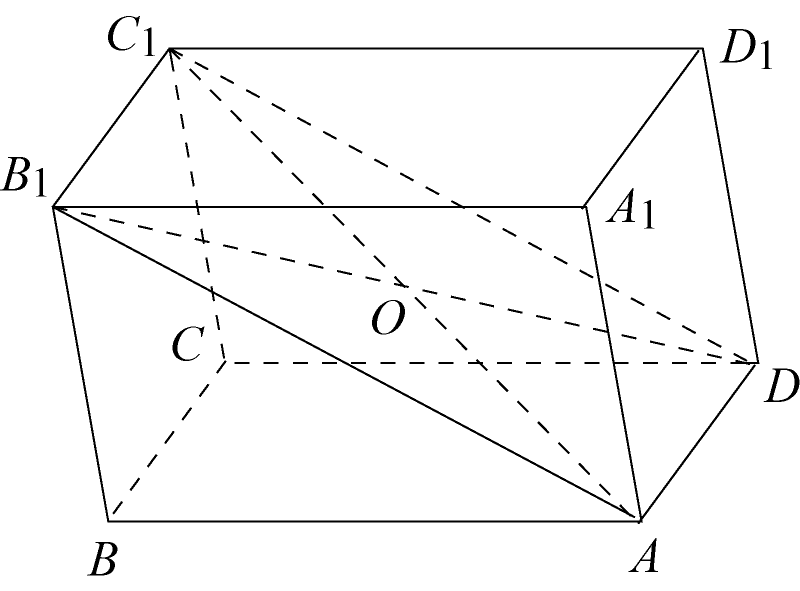
Доказательство. Рассмотрим две произвольные диагонали, например, и . Т.к. гранями параллелепипеда являются параллелограммы, то и , а значит по Т о двух прямых параллельных третьей . Кроме того это означает, что прямые и лежат в одной плоскости (плоскости ). Эта плоскость пересекает параллельные плоскости и по параллельным прямым и . Таким образом, четырехугольник – параллелограмм, а по свойству параллелограмма его диагонали и пересекаются и точкой пересечения делятся пополам, что и требовалось доказать.

Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани – прямоугольники. Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями). Таких размеров три (ширина, высота, длина).

Теорема 13.3. В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений (доказывается с помощью двукратного применения Т Пифагора).

Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.

Задачи

1. Сколько диагоналей имеет n-угольная призма

2. В наклонной треугольной призме расстояния между боковыми ребрами равны 37, 13 и 40. Найти расстояние между большей боковой гранью и противолежащим боковым ребром.

3. Через сторону нижнего основания правильной треугольной призмы проведена плоскость, пересекающая боковые грани по отрезкам, угол между которыми . Найти угол наклона этой плоскости к основанию призмы.

4. Сторона основания правильной четырехугольной призмы равна 15, высота равна 20. Найдите кратчайшее расстояние от стороны основания до не пересекающей ее диагонали призмы.

5. Плоскость, проходящая через сторону основания правильной треугольной призмы и середину противолежащего ребра, образует с основанием угол 45^о. Сторона основания равна . Найдите боковую поверхность призмы.

6. Боковое ребро прямого параллелепипеда равно 5, стороны основания –6 и 8, а одна из диагоналей основания – 12. найти диагонали параллелепипеда.

7. Ребро куба равно . Найдите расстояние от вершины куба до его диагонали, соединяющей две другие вершины.

8. Диагонали трех граней прямоугольного параллелепипеда, сходящиеся в одной вершине, равны , и 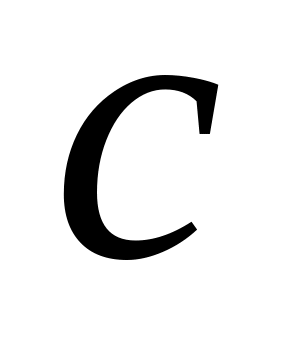. Найти линейные размеры параллелепипеда.

9. Доказать, что в кубе диагональ перпендикулярна плоскости .

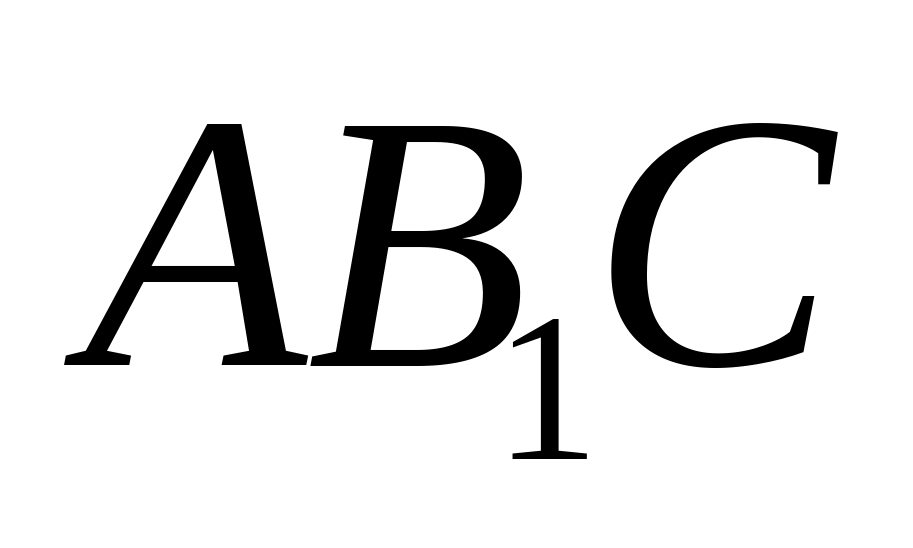10. Грани куба равны . Найти расстояние между скрещивающимися диагоналями и граней куба.