1.1.3 Определение допускаемого напряжения по заданной диаграмме материала сталь 35 (закалка с охлаждением в воде)

Для определения важнейших механических характеристик конструкционных материалов чаще всего используются испытания на растяжение. Для получения сравнимых результатов испытанию на растяжение подвергают образцы, форма, размеры и условия, нагружения которых определяются стандартом ГОСТ 1497-61.

Данный образец изготовлен из материала: сталь 35 (В35).

Результаты испытания образца на растяжение представлены диаграммой, выражающей зависимость удлинения от нагрузки (рис.1.3).

Для заданной диаграммы требуется:

1. Определить геометрические характеристики при заданных ,

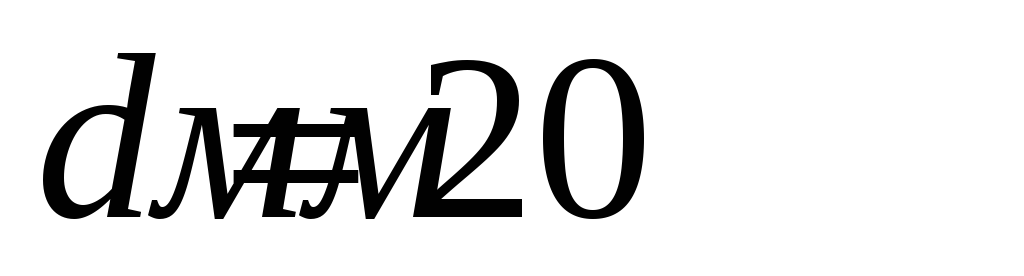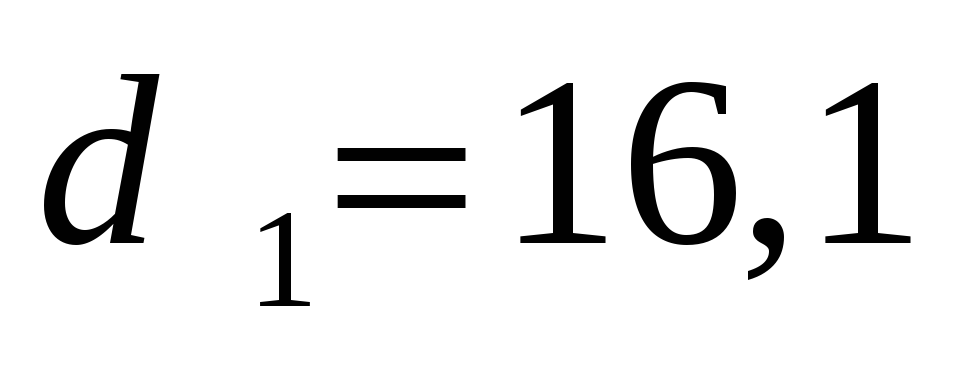
2. Вычислить основные механические характеристики

3. Выбрать коэффициент запаса прочности и определить допускаемое напряжение.

II. Индивидуальные задачи

2.1 Статически определимые системы

Проверить прочность и жесткость стержневой системы, если вертикальное перемещение узла В не должно превышать величины .Дано: ,,,,,,,,.

2.2 Статически неопределимые системы

Чугунный круглый стержень вставлен в стальной цилиндр, причем длина стержня больше длины трубки на , а площади их сечений одинаковы, т.е. . Подобрать площади сечений с таким расчетом, чтобы после приложения силы в стержне и трубке возникли напряжения одинаковой величины, если ,,.

1.1 Расчёты на растяжение

1.1.1 Центральное растяжение и сжатие ступенчатого бруса.

Дано: q = 600 , a = 1м, ,

1.1.1.1. Определение опорной реакции.

Уравнение равновесия в проекции на ось z (рис. 1.1, а):

2. Построение эпюр продольных сил, напряжений и перемещений.

Эпюра N_Z (рис. 1.1, б):

Эпюра σ_z (рис. 1.1, в):

Эпюра W (рис. 1.1, г):

2. Подбор сечений.

Из условия прочности на растяжение

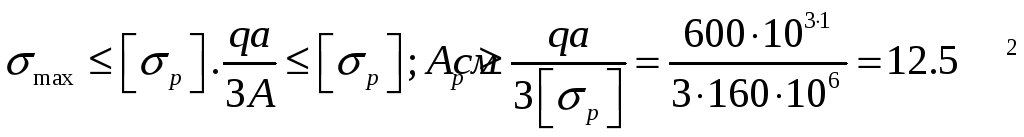
Из условия прочности на сжатие

Полное удлинение ступенчатого бруса

1.1.2 Расчёт простейших статически неопределимых стержневых

систем.

Дано:

1. Степень статической неопределимости.

Данная система (рис. 1.2, а) является однажды неопределимой.

2. Определение усилий, возникающих в стержнях 1 и 2.

Уравнение статики: (1);

Уравнение совместности деформаций:

Из подобия и (рис. 1.2, б) имеем:

Из (1) и (2)

3. Подбор сечений стержней.

1 вариант

2 вариант

Окончательно принимаем первый вариант, т.к. он обеспечивает и прочность обоих стержней, и заданное соотношение площадей.

1 стержень – 2 уголка , для выбранных уголков перегрузка составляет 4,8%

2 стержень – 2 уголка , для выбранных уголков перегрузка составляет 3,8%

4. Определение грузоподъёмности конструкции.

Уравнение предельного равновесия (рис. 1.2, в):

При переходе от метода допускаемых напряжений к методу допускаемых нагрузок можно повысить грузоподъёмность конструкции

в раза или на 4%.