Курсовая работа [вариан 8]1 / Задания и расчеты 2

2.1 РАСЧЕТ БАЛОК НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ

2.1. . Проектирование стальной балки в пяти вариантах

поперечного сечения

2.1.1 Построение эпюр Q_{y ,} М_{x .}

2.1.2 Спроектировать стальную балку (рис.2.1) в 5 вариантах поперечного сечения: круглого, прямоугольного(h/b=2),двутаврового, из двух швеллеров и двух равнобоких уголков, приняв допускаемое напряжение []=160МПа.

2.1.3 Оценить экономичность всех пяти сечений и начертить их в одном масштабе. 2.1.4 Для балки двутаврового профиля построить эпюры нормальных и касательных напряжений, а также исследовать аналитически и графически напряженное состояние в точке К (табл.2.1)опорного сечения.

Таблица 2.2

Исходные данные для расчета

Вариант		1	2	3	4	5	6	7	8	9	10
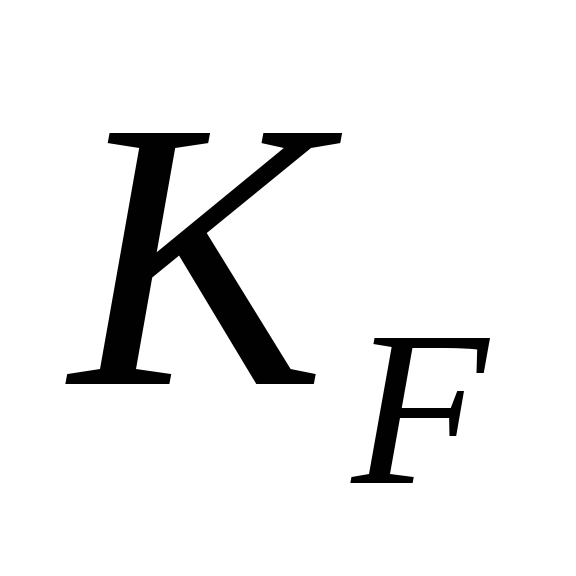
		3	2	4	1	3	2	4	3	2	1
		1	3	2	4	2	4	1	3	2	3
q, кН/м		12	20	16	18	14	15	10	22	20	12
а, м		1.0	0.8	1.2	1.0	1.2	1.2	1.0	0.8	1.0	1.5
l/[f]		500	600	800	1000	900	800	1000	600	800	500

Таблица 2.3

Номер схемы (рис. 14.9)	1	2	3	4	5	6	7	8	9	10
	11	12	13	14	15	16	17	18	19	20
	21	22	23	24	25	26	27	28	29	30
yК / h	0,1	0,2	0,25	0,3	0,4	-0,1	-0,2	-0,25	-0,3	-0,4

2.2.

Подобрать сечение балки(рис.2.3),удовлетворяющее условиям прочности и жесткости и допускаемое напряжение материала определяется исходя из диаграммы растяжения, выдаваемой преподавателем. Исследование перемещений выполнить тремя методами:

- пользуясь методом начальных параметров, определить прогибы и углы поворота сечений балки с координатами z = 0, a, 2а, 3а, 4а, 5а; изобразить изогнутую ось балки и показать на ней найденные перемещения;

- определить прогибы в середине пролета и на концах консолей, а также углы поворота на опорах энергетическим методом.

- используя любой численный метод (МКР или МКЭ), определить перемещения в 25…30 точках с применением ЭВМ.

2.1 Проектирование стальной балки в пяти вариантах

поперечного сечения

1.1. Построение эпюр Q_y и M_x. Опорные реакции

Y_i = 0,

m_A = 0,

Эпюра Q_y. Она строится по формуле Q = Q_O  qz. В данном случае следует взять знак ”минус”, так как погонная нагрузка направлена вниз. Поперечная сила постоянна на участках АВ, ВС, CD (q = 0) и изображается наклонной прямой на участке DE (q = const). Вычисляем значения Q_y в характерных точках

Q_A = R_A = 2qa, Q_AB = Q_A - qa = qa, Q_B = Q_AB = -qa,

Q_CD = Q_C - qa = 0 и строим ее эпюру.

Эпюра М_x. Она строится по формуле M_x = M_О + Q_Oz – 0,5qz². Изгибающий момент изменяется по квадратичному закону на участке DE (q = const) и по линейному закону – на всех остальных участках, где q = 0. По значениям момента в характерных точках

M_A = -4qa², M_AB = M_A +2 qaa = -2qa²,

M_BC = M_AB - qaa = -3qa², M_CD = M_CB - qa² = -4qa²,

строим эпюру M_x. Расчетный изгибающий момент равен

М_рас = М_A = 4qa² = 4151.2² = 72 кНм.

1.2. Подбор сечений. Из условия прочности по нормальным напряжениям _max = M_рас / W_x  [] определяем требуемый момент сопротивления поперечного сечения

W_x  M_рас / [] = 7210³ / 16010⁶ = 450 см³,

по которому подбираем конкретные сечения.

Круг: W_x = d³ / 32,

см.

Принимаем по ГОСТ 6636-86 нормализованное значение d_o = 170 мм, тогда см².

Прямоугольник (h / b = 2): W_x = b(2b)²/6 = 2b³/3,

см.

Ближайшее меньшее стандартное значение равно b_o = 85 мм. При этом балка будет работать с перенапряжением, равным

,

что недопустимо. Поэтому принимаем ближайший больший размер b_o = 85 мм, для которого см².

Двутавр. По ГОСТ 8239-89 выбираем двутавр №27a, для которого см³, А₃ = 43,2 см².

Два швеллера. По ГОСТ 8240-89 выбираем два швеллера №22a, для которых см³, А₄ = 228,8 = 57.6 см².

Неравнобокие уголки. Они находятся подбором, так как в сортаменте не даны значения момента сопротивления. Используя формулу W_x = 2I_x / y_наиб = 2I_x / (B – y_o), сделав несколько попыток, выбираем два уголка 25016012, для которых см³, А₅ = 263.6 = 127. см².

1.3. Оценка экономичности подобранных сечений. Масса балки определяется как произведение плотности материала на ее объем m = Al, т.е. расход материала при прочих равных условиях зависит только от площади поперечного сечения А. Сравнивая массы балок

m₁ : m₂ : m₃ : m₄ : m₅ =

= A₁ : A₂ : A₃ : A₄ : A₅ = 1 : 0,97 : 0,26 : 0,34 : 0,76,

заключаем, что самым неэкономичным является круглое сечение. При замене круга другими формами (прямоугольник, двутавр, два швеллера, два уголка) достигается экономия, равная соответственно 26%, 97%, 97% и 76%.

1.4. Исследование напряжений в опорном сечении для балки двутаврового профиля №27, параметры которой по ГОСТ 8239-89 равны:

h = 27 см, b = 13,5 см; d = 0,6 см; t = 10.2 см;

I_x = 5500 cм⁴; S_x = 229 cм³.

Внутренние силовые факторы в опорном сечении А:

Q_A = qa = 151.2 = 18 кН;

М_А = -4qa² = -4151.2² = -72 кНм.

Эпюра . Нормальные напряжения в поперечном сечении изменяются по линейному закону _z = (M_x / I_x)y. Вычисляем напряжения в крайних точках

_max = -_min = M_x / W_x = 7210³ / 45010^-6 = 160 МПа

и строим эпюру .

Эпюра . Она строится по формуле Журавского

.

Находим значения  в 4 характерных точках по высоте сечения (необходимые вычисления представлены в табл. 14.8) и строим эпюру касательных напряжений.

Таблица 14.8

№ точек	bi, см	, см3			i, МПа	max
1, 1	13,5	0	0	0	0
2, 2	13,5	159	11,7	0,0014	0,002
3, 3	0,6	159	265,4	0,003	0.045
4	0,6	229	381	1,0	12

Определение главных напряжений в точке К (y_к = -0,1h):

• напряжения в поперечном сечении

_к = (M_A / I_x)y_к = (-7210³ / 550010^-8)0,12710^-2 = -35 МПа,

_к = Q_A/(b_кI_x) = 1810³22910^-6/(0,610^-2550010^-8) = 12 МПа;

• величины главных напряжений

,

₁ = 0.04 МПа; ₃ = -35,04 МПа;