Решения задач / Rucov2 / РУК12
.DOCоткуда Iv = I + I - Iu = 204 + 667 – 121 = 750 см4.
Таким образом, центробежный момент уголка будет равен
I = 0,5(121-750)(-0,677) = 213 см4.
Пример 3.6Определить центробежный момент инерции равнобокого уголка 100х100х10 относительно центральных осей, параллельных полкам. РешениеПо таблице сортамента |
Рис. 3.14 |
прокатной
стали в соответствии
с ГОСТ 8509-72 (СТ
СЭВ 104-74) имеем
![]() =284
см4,
=284
см4,
![]() =74,1
см4,
=74,1
см4,
![]() =3,84
см,
=3,84
см,
![]() =1,96
см.
=1,96
см.
Пользуясь формулой поворота, находим
![]() ,
,
![]() cм4.
cм4.
Пример 3.7Определить положение главных центральных осей и величины главных центральных моментов инерции сечения, приведенного в примере 3.2. Решение1. Определение моментов инерции относительно центральных осей хСy. По таблице сорта- |
Рис. 3.15 |
мента имеем:
-
швеллер № 22:
I1 = 2330 cм4, I1 = 187 cм4, А1 = 28,8 см2;
-
уголок 100х100х10:
I2 = I2 = 179 cм4, А2 = 19,2 см2; центробежный момент инерции уголка относительно I22 = 105 cм4.
Учитывая, что центральные оси xy проведены параллельно собственным осям элементов фигуры, для вычисления осевых и центробежного моментов инерции всего сечения воспользуемся формулами (3.11), представляя все необходимые вычисления в табличной форме:
Таблица 3.4
|
Ном э л емен т а |
Координаты центра тяжести, см |
Пл о щ а д ь Аi, см4 |
Моменты инерции площадей, см4 |
|||||||||
|
|
|
|
||||||||||
|
xi |
yi |
Ii |
|
Ixi |
Ii |
|
Iyi |
Iii |
xiyiAi |
Ixiyi |
||
|
1 |
-2, 12 |
-3, 27 |
28,8 |
2330 |
308 |
2638 |
187 |
129 |
316 |
0 |
200 |
200 |
|
2 |
3, 17 |
4, 90 |
19,2 |
179 |
461 |
640 |
179 |
193 |
372 |
105 |
298 |
403 |
|
|
48 |
2509 |
769 |
3278 |
366 |
322 |
688 |
105 |
498 |
603 |
||
2. Определение главных центральных моментов инерции сечения. По формуле (3.18) имеем
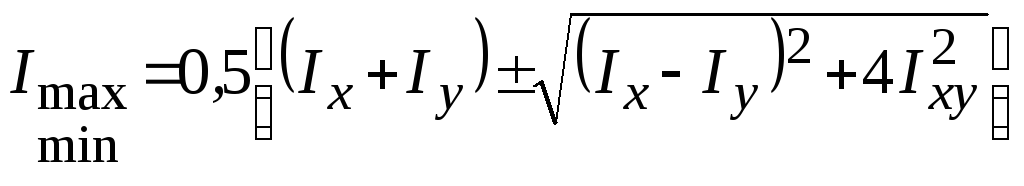 ,
,
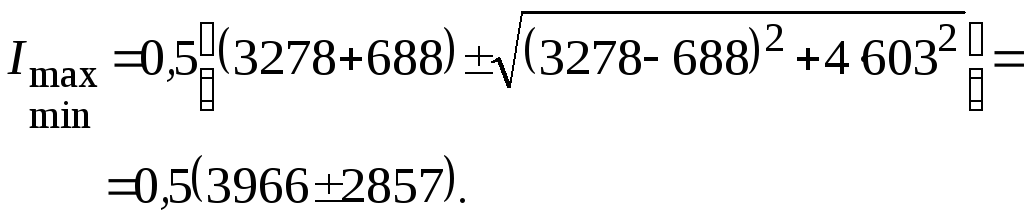
Отсюда Imax = I1 = 3412 см4, Imin = I2 = 555 см4.
Ориентация максимальной главной оси определяется по формуле (3.20)
tg1 = (Ix-I1)/Ixy = (3278-3412)/603 = -0,222,
откуда 1 = -1230.
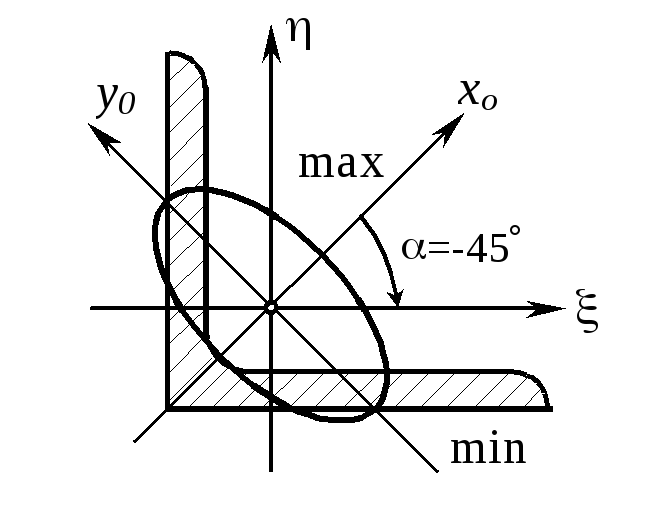
3. Построение эллипса инерции. Главные радиусы инерции равны
![]() см;
см;
![]() см.
см.
Отложив радиусы инерции перпендикулярно к соответствующим осям в том же масштабе, в каком вычерчена фигура, строим на них, как на полуосях, эллипс инерции.
СОДЕРЖАНИЕ
|
1. ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ ………….. |
53 |
|
1.1. Общие сведения ………………………………….… |
53 |
|
1.2. Линейное напряженное состояние ………………... |
56 |
|
1.3. Плоское напряженное состояние ………………….. |
59 |
|
1.4. Объемное напряженное состояние ……………….. |
66 |
|
1.5. Гипотезы прочности ……………………………….. |
69 |
|
2. КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ ……………………….. |
74 |
|
2.1. Краткие сведения из теории ……………………….. |
74 |
|
2.2. Примеры расчета …………………………………… |
77 |
|
3. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ …………………………………... |
85 |
|
3.1. Статические моменты. Определение положения центра тяжести ……………………………………... |
85 |
|
3.2. Моменты инерции ………………………………….. |
88 |
|
3.3. Преобразование моментов инерции при параллельном переносе осей …………………….………. |
89 |
|
3.4. Преобразование моментов инерции при повороте осей ………………………………………………….. |
93 |