
Решения задач / Rucov3 / РУК15
.DOC|
Рис. 25 |
Пример 17. Определить главные напряжения в точке К консольной балки (рис. 26), нагруженной сосредоточенной силой F = 50 кН, приложенной на свободном конце, если l = 50 см, С = 20, d = 4 см, b = 4 см, h = 10 см.
Решение. 1. Определение внутренних силовых факторов в поперечном сечении, проходящем через точку К. Строим эпюры Qy и Mx и находим QK = -F = -50 кН,
MK = -FC = -50 20 10-2 = -10кНм.
|
|
2. Определение главных напряжений. Напряжения в поперечном сечении определяются по формулам
Вычисляя
|
![]() ,
находим
,
находим
![]() ,
,
![]() .
.
Величины главных напряжений
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Направление главного растягивающего напряжения 1 по отношению к продольной оси балки z:
![]() ;
;
![]() ,
,
а напряжение 3 направлено перпендикулярно к 1.
Графическое определение величин главных напряжений и направлений главных осей представлено на рис. 27.
|
3. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ И РАСЧЕТ НА ЖЕСТКОСТЬ
3.1. Основные понятия
|
Рис.28 |
При изгибе произвольное сечение K балки (рис. 28) получает три перемещения: вертикальный прогиб V, горизонтальное смещение W, угол поворота . Ось деформированной балки называется упругой |
линией. В реальных конструкциях WV, Vmax l/200, max 1 (0,0174 рад), поэтому в расчетах можно пренебречь смещением W, а для углов поворота использовать приближенную формулу tg = dv/dz. Таким образом, для определения линейных и угловых перемещений сечений балки необходимо знать уравнение упругой линии V(z).
Кривизна оси балки связана с изгибающим моментом выражением K = 1/ = Mx/(EIx).
Из
курса математики известна следующая
формула для кривизны
линии:
![]() ,
,
где
![]() ,
,
![]() .
.
Подставляя это значение К в предыдущее выражение, получим точное дифференциальное уравнение упругой линии балки:
![]() .
(10)
.
(10)
Пренебрегая
![]() по сравнению с единицей, заменяем его
приближенным уравнением
по сравнению с единицей, заменяем его
приближенным уравнением
![]() (11)
(11)
которое называют основным дифференциальным уравнением упругой линии балки.
Выбор
знака определяется принятой системой
координат (рис. 29). Если ось y
направлена вверх, то знаки момента Мх
и кривизны
![]() совпадают, поэтому в уравнении (11) берется
знак “плюс”. При обратном направлении
оси y
знаки Мх
и
совпадают, поэтому в уравнении (11) берется
знак “плюс”. При обратном направлении
оси y
знаки Мх
и
![]() противоположны,
следовательно, в этом случае следует
использовать уравнение вида
противоположны,
следовательно, в этом случае следует
использовать уравнение вида
![]() ,
которое и рассматривается в дальнейшем.
,
которое и рассматривается в дальнейшем.
|
Рис. 29 |
3.2. Метод начальных параметров
Последовательно интегрируя уравнение (11), получим сначала выражение для углов поворота
![]() (а)
(а)
а затем для прогибов
 .
(б)
.
(б)
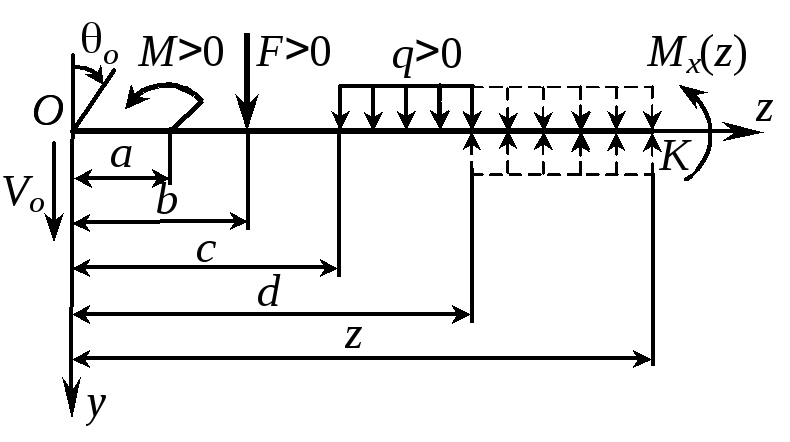
Для вычисления интегралов, входящих в формулы (а) и (б), запишем выражение изгибающего момента Мх(z) от типичных нагрузок (рис. 30):
![]() .
.
|
Рис. 30 |
Рис. 31 |
Подставляя Мх в формулы (а) и (б) и учитывая, что в общем случае на балку действует несколько моментов, сосредоточенных сил и погонных нагрузок, после интегрирования получим окончательно
![]() ,
,
(12)
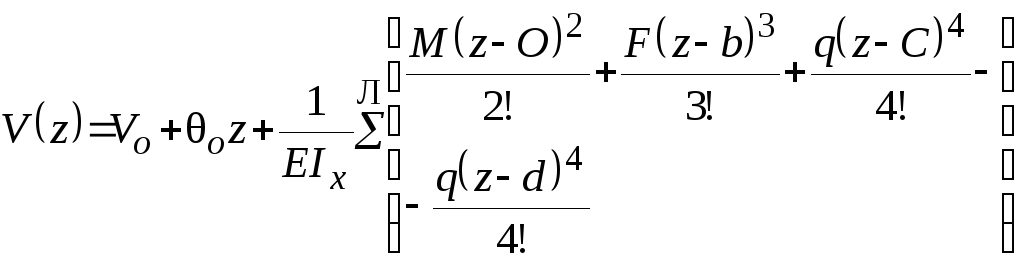 (13)
(13)
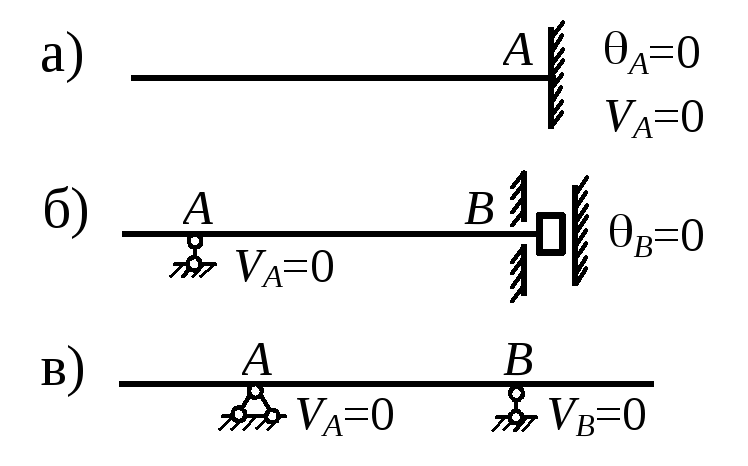
Здесь о и Vo – угол поворота и прогиб в начале координат, называемые начальными параметрами и определяемые из условий опирания балки (рис. 31). Значок “Л” над символом суммы обозначает, что суммируются только те величины, которые относятся к части балки, расположенной слева от того сечения, где ищутся перемещения. Все нагрузки, приведенные на рис. 30, считаются положительными.
|
Пример 18 Элемент машины представляет собой балку пролетом 3a, опирающуюся на шарнирно подвижную опору, а с другой – на вертикальные направ- |
Рис. 32 |
ляющие, вдоль которых свободно (без трения) скользит ползун, жесткосвязанный с балкой. Определить прогибы в точках А и С и угол поворота на опоре В.
Решение. 1. Определение опорных реакций. Составляем уравнения равновесия и находим искомые реакции:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2. Определение начальных параметров. Из условий опирания балки имеем А = 0 и VВ = 0. Из первого получаем о = 0, а из второго находим Vо:
![]() ,
,
![]() .
.
3. Определение искомых перемещений. Имеем
![]() ;
;
![]() ,
,
![]() .
.
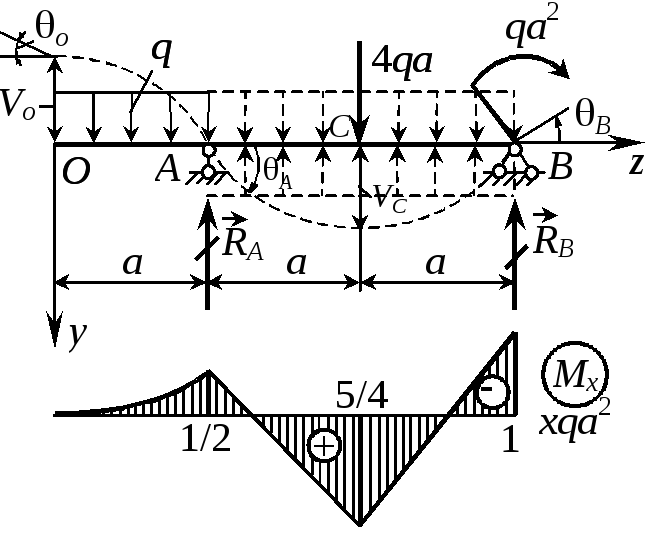
Пример 19. Определить углы поворота опорных сечений и прогибы на конце консоли и в середине пролета. Построить пунктиром вид изогнутой оси балки (рис. 33).
Решение. 1. Определение опорных реакций. Из уравнений равновесия имеем
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
|
Рис. 33 |
2. Определение начальных параметров. Из условий опирания балки VA = VB = 0 или в развернутом виде
|

Таким образом, получаем систему

откуда
![]() ,
,
![]() .
.
3.
Определение искомых перемещений. Угол
поворота на опоре А
![]() .
.
Угол поворота на опоре В
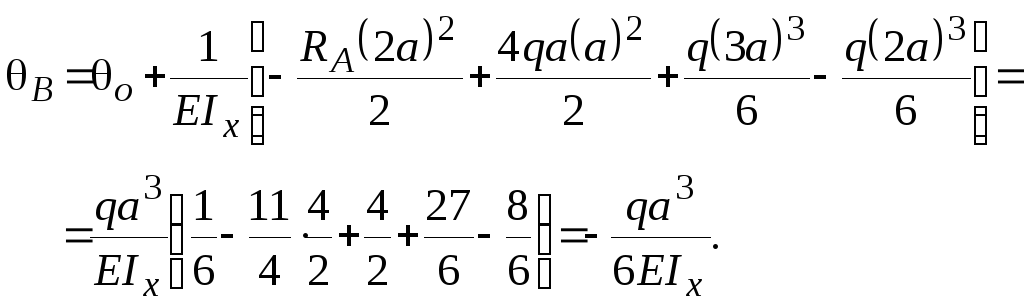
Прогиб посредине пролета (сеч. С)

Примерный вид упругой линии балки показан на рис. 33 пунктиром.


 Рис.
26
Рис.
26 Рис.
27
Рис.
27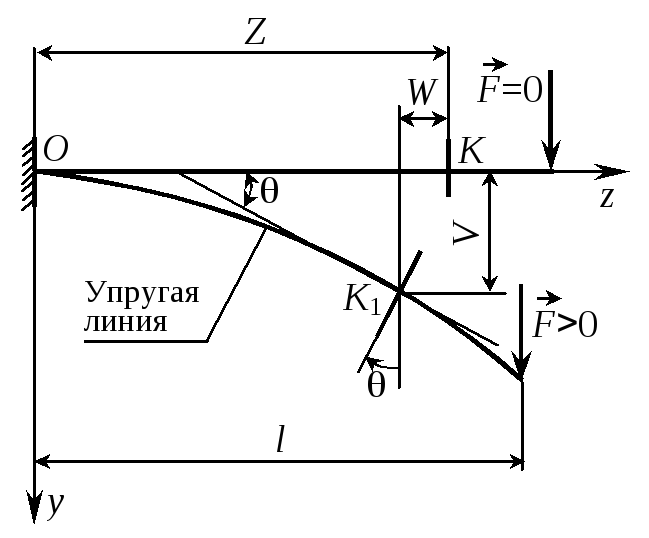


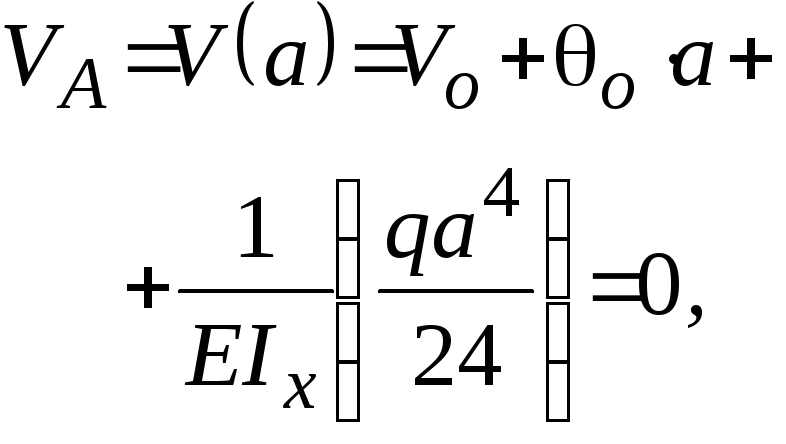 ,
,