
Решения задач / Rucov3 / РУК14
.DOC|
Рис. 13 |
Пример 10Тонкая стальная полоса, имеющая поперечное сечение размером 0,8х25 мм и длину l = 25 см, изгибается сосредоточенными моментами, приложенными на концах, в дугу |
окружности, опирающуюся на угол , равный 1 радиану. Чему равно максимальное напряжение в полосе?
Решение. Изгибающий момент связан с кривизной соотношением I/ = Mx/EIx, откуда Mx = EIx/.
Максимальное напряжение max = Mx/Wx = EIx/(Wx)
или, учитывая, что l = и = l/, Ix/Wx = ymax = h/2,
получим max = Eh/(2l) = 2001090,8/(2250) = 320 МПа.
Пример 11. Шарнирно опертая по концам стальная балка с поперечным сечением из двух швеллеров № 20а нагружена, как показано на рис. 14. Определить величину допускаемой нагрузки q, если а = 1 м, [] = 150 МПа.
Решение
Опорные реакции: mB = 0, RA6a = = q4a4a + 2qa2 - 2qa2a- - q2aa = 0, RA = 2qa; |
|
mA = 0, RB6a = q2a5a + 2qa2-q4a2a + 2qa4a = 0, RB = 2qa.
Проверка:
Yi = 0, -RA+ q4a-2qa-q2a+RB = -2qa+4qa-2qa-2qa+2qa = 0.
Эпюры Q и М строим по характерным точкам.
Расчетный изгибающий момент Мmax = 2qa2.
|
2. Определение допускаемой нагрузки. Геометрические характеристики сечения. Из таблиц сортамента согласно ГОСТ 8240-72 имеем для швеллера № 20а: |
Рис. 15 |
I = Iy = 139 cм4; А = 25,2 см2; zo = 2,28 cм; b = 8 см.
По формуле параллельного переноса осей момент инерции сечения относительно центральной оси х равен Ix = 2[I + (b - zo)2A], откуда момент сопротивления
Wx = Ix/ymax = 2[I +(b-zo)2A]/b = 2[139+(8-2,28)225,2]/8 = 241 см3.
Из условия прочности балки Мmax/Wx = 2qa2/Wx [],
oткуда [q] = []Wx /2a2 = 15010624110-6/(212) = 18 кН/м.
|
Пример 12 Подобрать необходимые размеры поперечного сечения балки, составленной из двух скрепленных бревен, если q = 26 кН/м, [] = 10 МПа, Q = 1 м. |
|
Решение
1. Построение эпюр Q и М.
Опорные реакции:
mB = 0, RA4a = 0,5qа2 + 2qa2a - qa0,5a, RA = qa;
mA = 0, RB4a = qa4,5a + 2qa2а - 0,5qа2, RB = 2qa.
Проверка:
Yi = 0, RA + RB - 2qa - qa = qa + 2qa - 2qa - qa = 0.
Строим эпюры q и М и находим расчетный изгибающий момент, равный Мmax = 1,5 qa2.
|
2. Подбор сечения балки. Геометрические характеристики. Сечение балки является составным, поэтому Ix = 2(I+y2A) = 2[d4/64+(d/2)2d2/4] = (5/32)d4, Wx = Ix/ymax = Ix/d = (5/32)d3. Из условия прочности балкиMmax/Wx ; 1,5qa2/(5d3/32) . |
Рис. 17 |
Отсюда
![]() .
.
Пример 13. Тензометр Т, установленный на стальной балке, имеет коэффициент увеличения k = 1000 и базу s = 20 мм. Показание тензометра равно n = 5 мм. Определить наибольшее нормальное напряжение в балке.
|
Рис. 18 |
РешениеНапряжение в балке на уровне тензометра Т равно, с одной стороны, Т = ЕТ = Еn/(ks), (a) C другой стороны, Т = (MT/Ix) yT. (б) Наибольшие нормальные напряжения возни- |
кают в крайних волокнах того же сечения, где приложена сила F, т.е.
max = (Mmax/Ix) ymax. (в)
Разделив (в) на (б), получим max = Т (Mmax/МТ)(ymax/yТ) = 4Т или с учетом (а)
max = 4Еn/(ks) = 42001095/(100020) = 200 МПа.
Пример 14Тележка перемещается вдоль балки длиной l = 10 м. На каждое колесо действует нагрузка F = 20 кН. Найти опасное положение тележки, при котором изгибающий момент будет иметь наи- |
Рис. 19 |
большее значение и определить наибольшее напряжение, полагая С = 2 м.
Решение
Очевидно, наибольший изгибающий момент возникает в сечении, расположенном под передним колесом тележки (сеч. D), где
MD = RB(l – z - C) = F(2z + C)(l – z - C)/l, RB = F(2z + C)/l.
Из условия экстремума
dMD/dz
= 0 находим опасное положение тележки
![]() ,
,
z4 = (2l-3c)/4.
В нашем случае z = (210 - 32)/4 = 3,5 м.
Наибольший изгибающий момент
Mmax = MD(z) = F(2z + c)(l - z - c)/l,
Mmax = 20(23,5 + 2)(10 - 3,5 - 2)/10 = 81 кНм.
Максимальное напряжение
max = Mmax/Wx = 81103/95310-6 = 85 МПа.
2.2. Касательные напряжения
Элементарная теория касательных напряжений, разработанная Д.И. Журавским, основывается на двух допущениях.
1. Касательные напряжения направлены параллельно поперечной силе Qy.
2. Касательные напряжения распределяются равномерно по ширине сечения.
Сделанных допущений достаточно, чтобы найти закон распределения касательных напряжений по высоте сечения. Проще всего вычислить эти напряжения через парные им касательные напряжения, возникающие в продольных сечениях.
|
|
Выделим из балки бесконечно малый элемент (рис. 20,г) и рассмотрим его равновесие в проекции на ось z:
![]()
![]() .
(а)
.
(а)
Вычисляя
![]() ,
,
![]() ,
,
![]() ,
,
![]()
и подставляя в
(а), получим
![]()
или с учетом
дифференциальной зависимости
![]()
![]() (8)
(8)
Рассмотрим конкретные сечения.
Прямоугольник (рис. 21,а). Имеем: by = b,
![]() ,
,
![]() .
.
Следовательно,
![]()
и
![]() .
.
Как видим, касательные напряжения изменяются по высоте сечения по закону квадратной параболы.
Для балки круглого сечения (рис. 21,б) аналогично можно найти
![]() и
и
![]() .
.
|
|
Пример 15. Определить касательное напряжение в точке К данного сечения, если поперечная сила равна Q = 500 кН.
|
Рис. 22 |
Решение
По формуле
Журавского имеем
Учитывая, что bK = 6 см,
|
![]() ,
,
получим
![]() .
.
Пример 16. Построить эпюры вертикальной составляющей касательного напряжения в частях от наибольшего значения max = о для указанных форм поперечного сечения балки.
|
Рис. 23 |
Nп/п |
by |
|
|
i/max |
|
1 |
0,5b |
0 |
0 |
0 |
|
|
2 |
0,5b |
3b3/16 |
3b2/8 |
1 |
|
|
3 |
b |
3b3/16 |
3b2/16 |
1/2 |
|
|
4 |
b |
5b3/16 |
5b2/16 |
5/6 |
|
|
3 |
b |
3b3/16 |
3b2/16 |
1/2 |
|
|
2 |
0,5b |
3b3/16 |
3b2/8 |
1 |
|
|
1 |
0,5b |
0 |
0 |
0 |
Для остальных сечений студентам предлагается построить эпюры самостоятельно.
|
|
2.3. Главные напряжения
В произвольной точке поперечного сечения балки, находящейся на расстоянии y от нейтральной оси, нормальные и касательные напряжения определяют по формулам
![]() ,
,
![]() .
.
Нормальные напряжения максимальны во внешних волокнах балки и равны нулю на нейтральной оси. Касательные напряжения равны нулю во внешних волокнах и обычно достигают максимума на нейтральной оси. При поперечном изгибе в плоскости yz x = y = 0, поэтому напряженное состояние является плоским и главные напряжения определяются по формулам
 ,
,
![]() .
(9)
.
(9)
Рассмотрим балку прямоугольного сечения и определим главные напряжения в нескольких характерных точках произвольного сечения mn (рис.25).


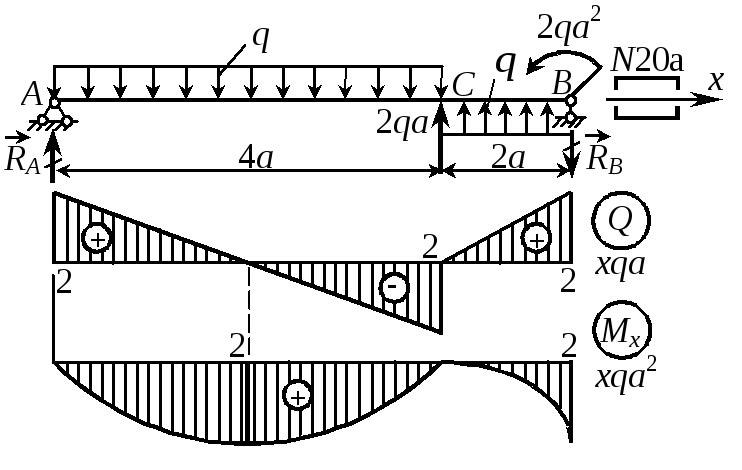 Рис.
14
Рис.
14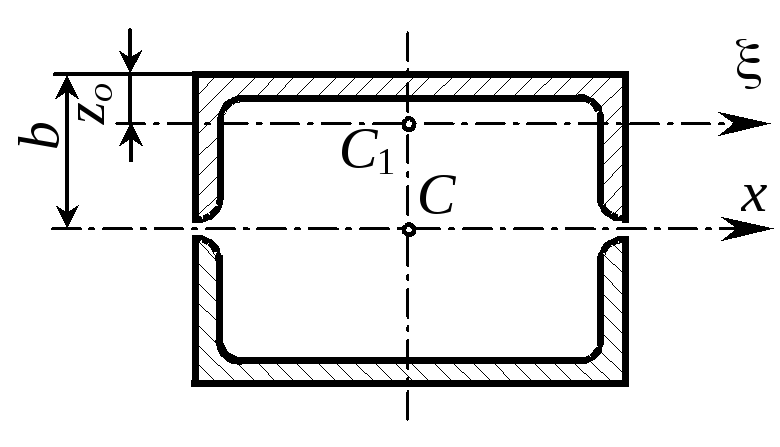
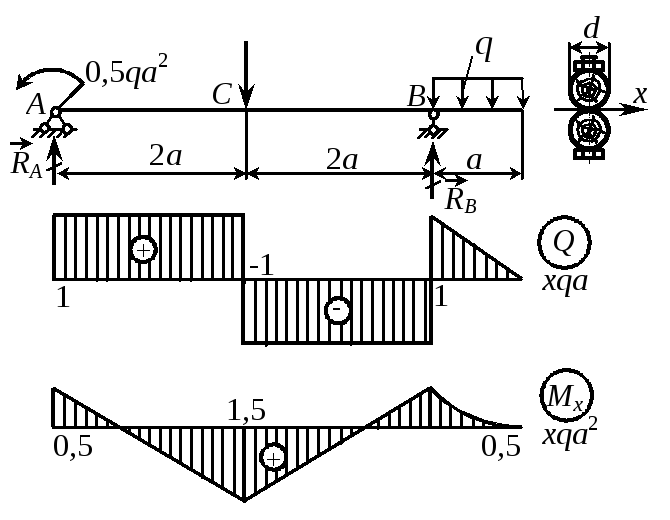 Рис.
16
Рис.
16
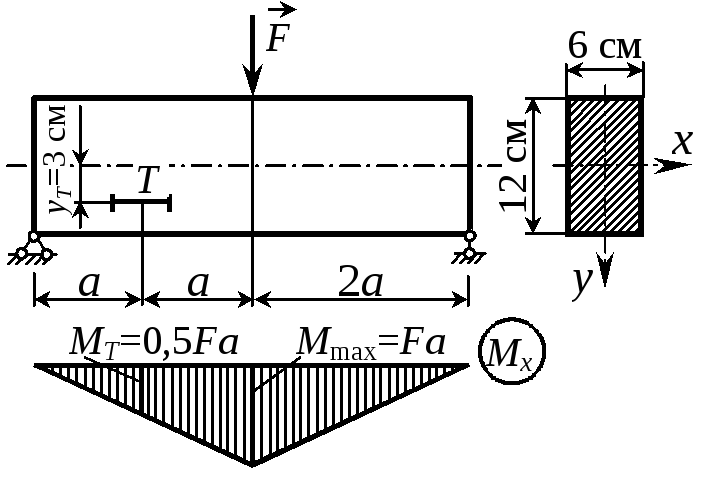
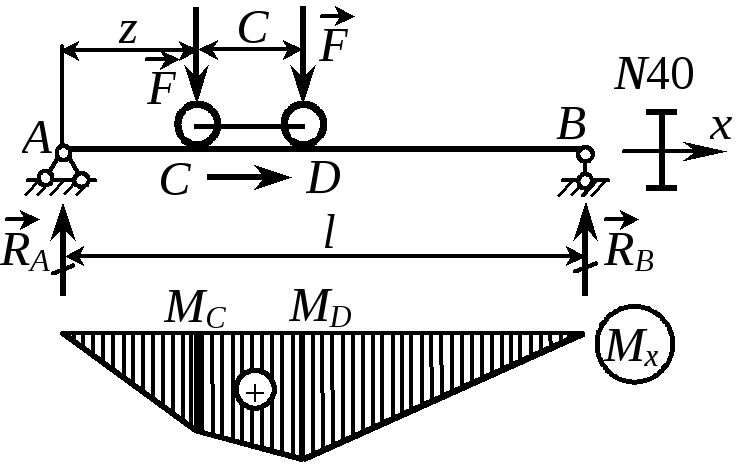
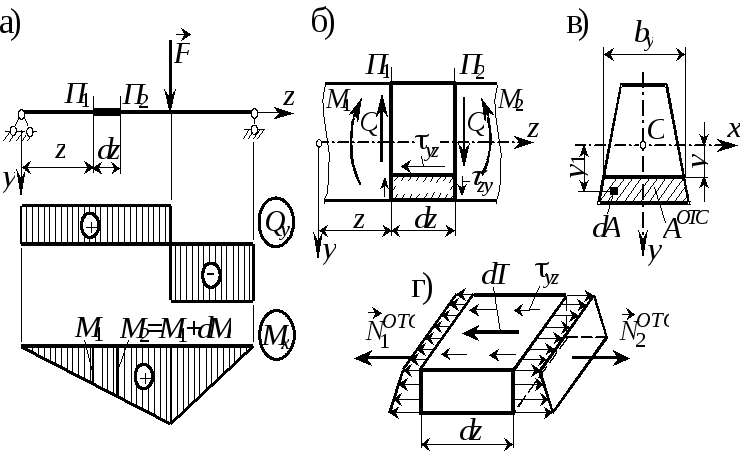 Рис.
20
Рис.
20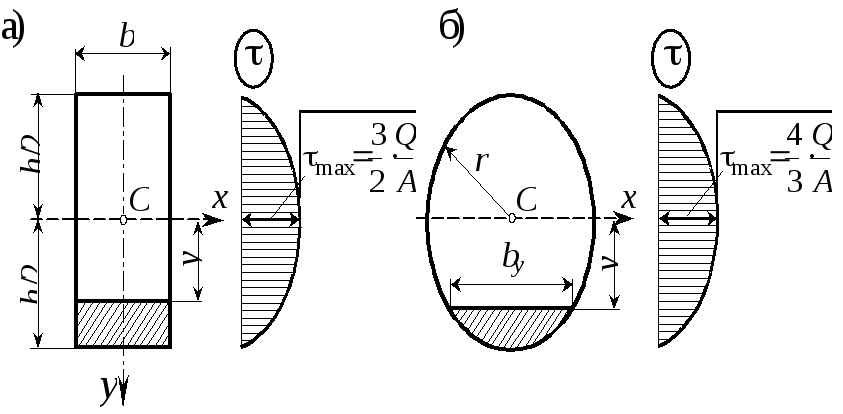 Рис.
21
Рис.
21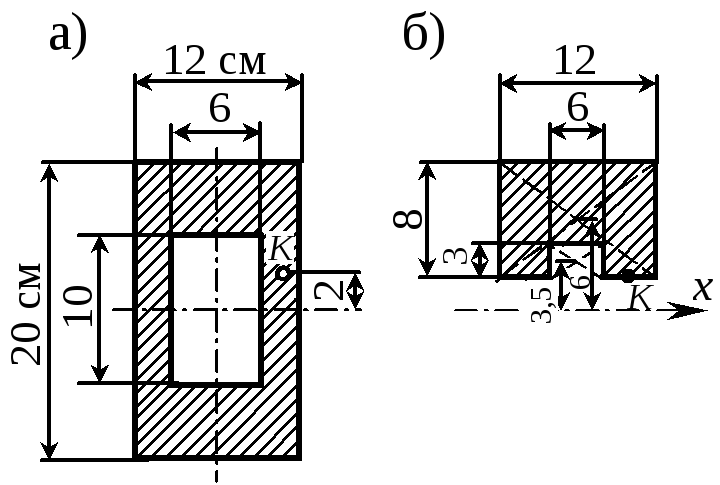
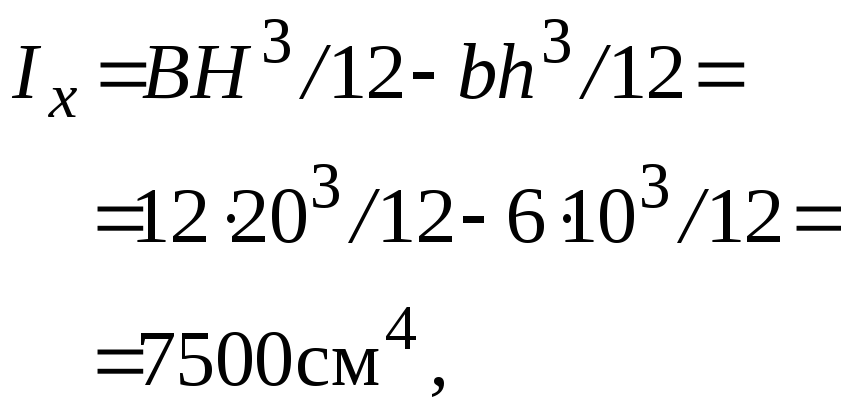
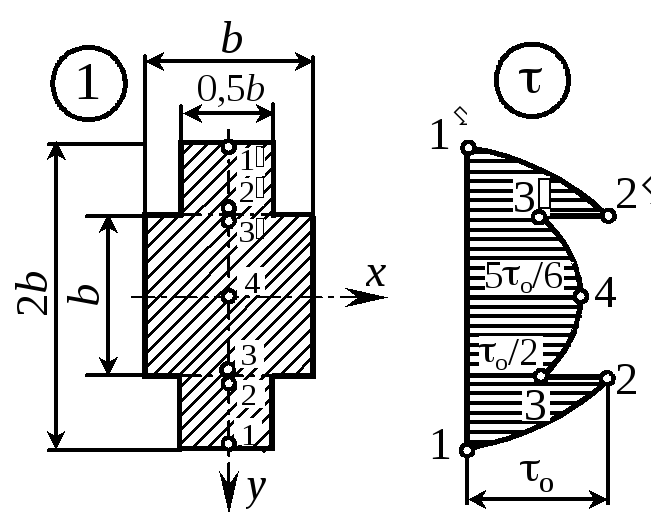
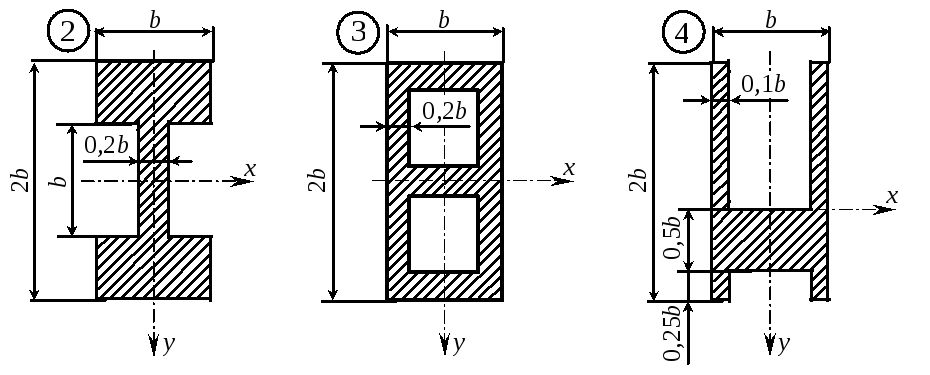 Рис.
24
Рис.
24