11. Плоскость в пространстве.

11.1 Общее уравнение плоскости. Зафиксируем декартову прямоугольную систему координат. Рассмотрим произвольное уравнение первой степени

. (*)

Заметим, что хотя бы один из коэффициентов не равен нулю (иначе это уравнение имело бы нулевую степень). Тогда уравнение (*) имеет хотя бы одно решение , т.е. существует хотя бы одна точка, координаты которой удовлетворяют уравнению (*): . (**)

Вычтем из уравнения (*) уравнение (**):

. (***)

Уравнение (***) эквивалентно уравнению (*), т.е. если координаты точки удовлетворяют уравнению (*), то они удовлетворяют уравнению (***), и наоборот.

Обозначим вектор с координатами . Пусть - плоскость, проходящая через точку и перпендикулярная вектору . Если точка лежит в плоскости , то вектор перпендикулярен вектору , скалярное произведение этих векторов равно 0. Тогда координаты точки удовлетворяют уравнению (***) и, следовательно, уравнению (*). Если же точка не лежит в плоскости , то векторы и не перпендикулярны, и скалярное произведение этих векторов не равно 0. Значит, в этом случае координаты точки не удовлетворяют уравнению (***) и уравнению (*).

Пусть теперь дана произвольная плоскость. Выберем вектор , перпендикулярный этой плоскости, и произвольную точку , лежащую в этой плоскости. Если произвольная точка плоскости, то векторы и перпендикулярны, их скалярное произведение равно 0. Тогда координаты точки удовлетворяют уравнению (***) и, следовательно, уравнению (*), являющимся уравнением первой степени. Мы доказали

Утверждение. Произвольная плоскость в пространстве определяется уравнением первой степени. Обратно, любое уравнение первой степени определяет в пространстве плоскость.

Уравнение (*) называется общим уравнением плоскости.

11.2. Нормированное уравнение плоскости. Заметим, что коэффициенты уравнения (*) определены с точностью до пропорциональности. Умножив все коэффициенты на одно и то же не равное нулю число, мы получим новое уравнение, но оно будет задавать ту же плоскость. Если потребовать, чтобы вектор нормали , который до сих пор был произвольным, имел единичную длину, т.е. , то он будет определен однозначно (с точностью до знака). Запишем теперь уравнение плоскости в таком виде: . Этот вид уравнения называют нормированным.

Выясним геометрический смысл коэффициента . Если точка лежит в плоскости , то из равенства с ледует, что . Так как вектор имеет единичную длину, то .

Значит, - это проекция любого радиус-вектора точки, лежащей на плоскости.

11.3. Уравнение плоскости в отрезках. Общее уравнение плоскости (*) называется полным, если все коэффициенты отличны от нуля. В противном случае оно называется неполным. Неполные уравнения задают плоскость, проходящую через начало координат, параллельную какой-либо координатной оси или параллельную какой-либо координатной плоскости. Все эти случаи несложно рассмотреть.

Мы же рассмотрим полное уравнение плоскости. Так как все коэффициенты общего уравнения отличны от нуля, его можно переписать в виде: ,

где . Этот вид уравнения плоскости называется уравнением плоскости в отрезках. Коэффициенты имеют прозрачный геометрический смысл: это длины отрезков, которые плоскость отсекает на координатных осях. Чтобы увидеть это, надо найти точки пересечения плоскости с координатными осями. Например, чтобы найти точку пересечения плоскости с осью , надо в уравнении плоскости в отрезках положить . Мы сразу же получим . Остальные точки пересечения находятся аналогично.

11.4. Уравнение плоскости, проходящей через три заданные точки.

Поставим задачу: написать уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой. Пусть эти точки заданы своими координатами: , , . Так как эти точки не лежат на одной прямой, то векторы и не коллинеарны. Тогда точка принадлежит той же плоскости, что и точки , тогда и только тогда, когда векторы , , компланарны. Это условие равносильно равенству нулю смешанного произведения этих векторов:

.

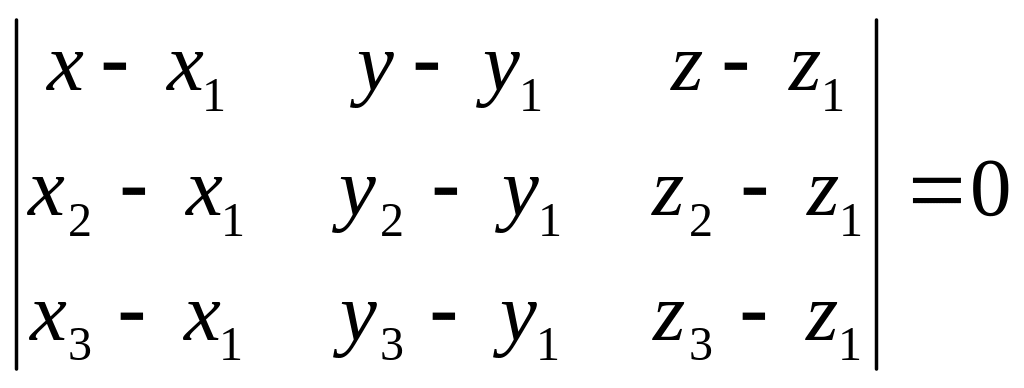Это уравнение является уравнением первой степени и дает нам искомое уравнение плоскости.

11.5. Угол между плоскостями. Пусть заданы две плоскости своими общими уравнениями: , .

Очевидно, что вопрос о нахождении угла между плоскостями сводится к нахождению угла между их нормалями:

.

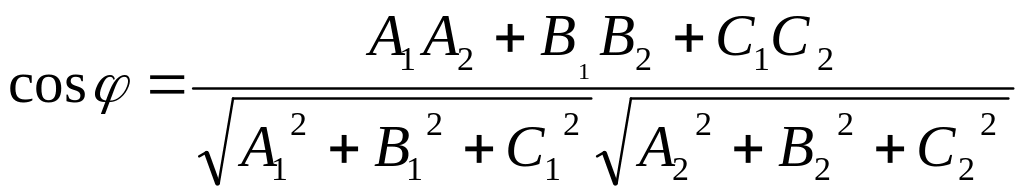Условие параллельности двух плоскостей сводится к вопросу о коллинеарности векторов нормали: плоскости параллельны тогда и только тогда, когда координаты векторов нормали пропорциональны.

Две плоскости перпендикулярны тогда и только тогда, когда перпендикулярны их нормали, т.е. скалярное произведение векторов нормали равно нулю:

.