16.3. Неравенство Коши - Буняковского.

Теорема. Для любых векторов и справедливо неравенство .

Доказательство. Так как скалярное произведение является положительно определенной формой, то .

При фиксированных векторах и мы имеем квадратный трехчлен от , дискриминант которого отрицательный или равен нулю: .

Отсюда или . Теорема доказана.

Следствие (неравенство треугольника). Для любых векторов и справедливо неравенство .

Доказательство:

следовательно, .

16.4. Угол между векторами. Заметим, что из неравенства Коши - Буняковского следует, что .

Это значит, что отношение является косинусом вполне определенного угла :

. Этот угол принято считать углом между векторами.

Определение. Векторы и называются ортогональными, если угол между ними равен , т.е. . Нулевой вектор ортогонален любому вектору.

Заметим, что из ортогональности векторов и следует теорема Пифагора:

.

Эту теорему можно обобщить на любое число попарно ортогональных векторов:

Задача. Докажите, что если , то векторы и ортогональны (диагонали ромба пересекаются под прямым углом).

16.5. Ортонормированные базисы.

Определение. Базис пространства называется ортогональным, если базисные векторы попарно ортогональны. Базис называется ортонормированным, если при этом базисные векторы имеют единичную длину.

Теорема. Любая ненулевые взаимно ортогональные векторы линейно независимы. Если , то эти векторы образуют ортогональный базис.

Доказательство. Пусть , причем . Тогда

, ,

, . Полученное противоречие доказывает теорему.

Теорема. В любом конечномерном пространстве существует ортонормированный базис.

Доказательство теоремы немедленно следует из того, что существует базис , в котором квадратичная форма, соответствующая скалярному произведению, имеет канонический вид , ( ). В этом базисе скалярное произведение векторов и задается формулой . Но это и означает, что базис ортонормированный.

16.6. Процесс ортогонализации Грама – Шмидта. Пусть - произвольный базис евклидова пространства. Мы будем строить новый – ортонормированный – базис пространства .

В качестве первого вектора нового базиса возьмем вектор . Таким образом, длина вектора равна 1. Прежде, чем построить второй вектор нового базиса, построим вектор : .

Вектор не может быть нулевым, поскольку векторы и линейно независимы. Заметим, что векторы и ортогональны. В качестве второго базисного вектора возьмем вектор . Теперь будем строить третий базисный вектор. Сначала возьмем вектор .

Этот вектор – ненулевой, так как векторы линейно независимы,- ортогонален векторам и . Остается только нормировать его: . Алгоритм ясен: имея вектор нового базиса, мы построим сначала вектор .

Этот вектор ненулевой и ортогональный векторам . Нормировав его, получаем -й вектор нового базиса .

16.7. Матрица Грама. Пусть - произвольный базис пространства. В этом базисе скалярное произведение, как и любая билинейная форма, имеет свою матрицу. Легко видеть, что это за матрица. Так как ,

то элементами этой матрицы являются скалярные произведения базисных векторов.

Определение. Матрицей Грама векторов называется матрица , элементы которой являются скалярными произведениями этих векторов: . Можно записать в матричном виде .

Очевидно, что матрица является симметричной с определителем, большим нуля.

Матрицу Грама можно построить не только для базисных векторов. Возьмем произвольные векторы и построим матрицу Грама аналогичным образом:

.

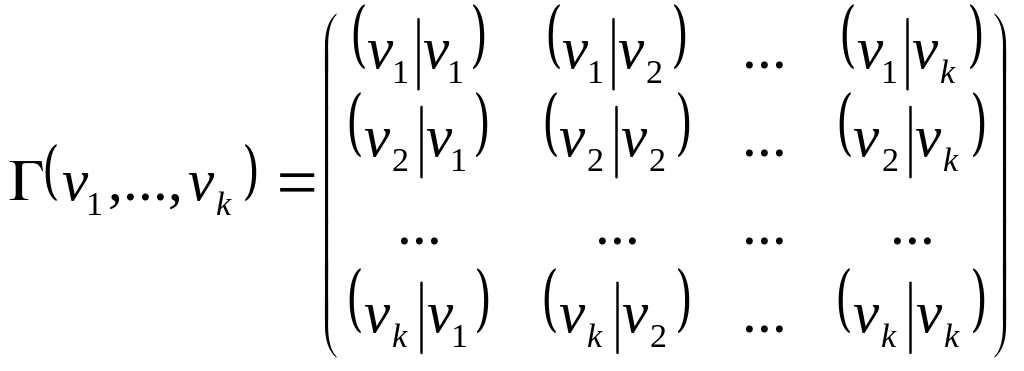Теорема. Определитель матрицы Грама произвольных векторов положителен, если эти векторы линейно независимы, и равен нулю в противном случае.

Доказательство. Если векторы линейно независимы, построим подпространство , в котором эти векторы будут базисом. (это подпространство является множеством всевозможных линейных комбинаций векторов ). Скалярное произведение, ограниченное на это подпространство, по-прежнему остается симметричной положительно определенной билинейной формой. Матрица Грама этих векторов является матрицей этой формы, поэтому ее определитель больше нуля.

Если векторы линейно зависимы, то один из них линейно выражается через другие, например, . Подставим в матрицу вместо вектора это выражение. Учитывая линейность скалярного произведения, получим, что первый столбец является линейной комбинацией остальных столбцов. Отсюда следует, что определитель матрицы равен нулю.

Следствие. Матрица Грама векторов ортонормированного базиса является единичной.

16.8. Переход от одного ортонормированного базиса к другому. Пусть - ортонормированный базис пространства, - некоторый другой ортонормированный базис. Переход от старого базиса к новому осуществляется с помощью матрицы перехода . Поскольку в ортонормированном базисе матрица скалярного произведения является единичной, то , или . Получается, что матрица является обратной л матрице : .

Определение. Матрица , для которой выполняется условие , называется ортогональной.

Ортогональные матрицы и только они являются матрицами перехода от одного ортонормированного базиса к другому.

Условие ортогональности матрицы можно записать через ее элементы:

Очевидным свойством ортогональных матриц является равенство 1 их определителя.

Задача. Докажите, что любая ортогональная матрица порядка 2 имеет вид

или .