3. Правая и левая системы координат на плоскости.

На рис. изображены два типа взаимного расположения координатных осей на плоскости. Если мы представим себя в роли наблюдателя, стоящего в начале координат и обращенного в сторону положитель­ной полуоси х, то в случае а) ось у будет идти справа налево, а в случае б) — слева направо; В первом случае координатную систему называют правой, во втором левой. Вообще, упорядочен­ную пару пересекающихся направлений на плоскости называют правой, если второе направление пересекает первое справа налево (по отношению к наблюдателю, обращенному в сторону первого на­правления), и левой, если второе направление пересекает первое слева направо. Для того чтобы, поворачивая на н аименьший угол, совместить первое направление со вторым, нужно в случае правой пары вращать его против часовой стрелки, а в случае левой пары — по часовой стрелке (черт. 5). Заметим, что, сравнивая направления осей на рис, мы предста­вляли себя находящимися с той стороны плоскости, в которую обра­щен чертеж. Если бы мы перевернули страницу и посмотрели на рис на свет, то ориентации координатных си­стем п еременились бы на обратные: правая представилась бы как левая, а левая — как правая.

4. Декартовы координаты в пространстве

Совершенно аналогично вводятся координаты в пространстве. А именно, берутся три координатные оси, пересекающиеся в одной точке и не лежащие в одной плоскости. Масштабные единицы на осях, вообще говоря, могут быть опять вы­браны различные. Кроме них, для из­мерения всех длин в пространстве выбирается общая «абсолютная масштабная единица», которой, в частности, измеряются и длины масштабных единиц на осях. В качестве начала отсчета на всех трех осях берется точка их пересечения О (начало координат). Одну из координатных осей называют осью абсцисс (осью х), другую — осью ординат (осью у) и третью — осью аппликат (осью z). Плоскость, проходящая через оси х и у, называется координатной плоскостью ху, плоскость, проходящая через оси у и z,—координатной плоскостью уz и плоскость, проходящая через оси х и z, — координатной плоскостью хz. Для того чтобы задать числами положение точки М в пространстве, проводят через эту точку плоскости, параллельные координатным плоскостям. Плоскость, параллельная координатной плоскости уz, пересечет ось абсцисс в некоторой точке М ; плоскость, параллельная координатной плоскости xz, пересечет ось ординат в некоторой точке М ; плоскость, параллель­ная координатной плоскости ху, пересечет ось аппликат в некоторой точке М . Пусть х, у, z— координаты точек М , М , М на соответствующих осях. Положение точки М вполне определяется заданием чисел х, у, z. Эти числа называются декартовыми коор­динатами точки М, при этом х — абсциссой, у — ординатой и z — аппликатой. Параллелепипед O М М М ABCM, высекаемый координатными плоскостями и параллельными им плоскостями, проходящими через точку М, называется координатным параллелепипедом точки М; его ребра (и в частности от­резки О М , М , М ) называются координатными отрезками точки М. Чтобы указать, что точка М имеет координаты х, у и z, пишут: M{x,y,z); при этом абсциссу поме­щают на первом месте, ординату — на втором и аппликату — на третьем. Точку с абсциссой х, ординатой у и аппликатой z записывают также символом (х,у, z). Таким образом, каждой точке пространства соответствует вполне определенная упорядоченная тройка вещественных чисел; обратно, каждой упорядочен­ной тройке вещественных чисел соответствует вполне определен­ная точка пространства. Иными словами, между совокупностью всех точек пространства и совокупностью всех упорядоченных троек вещественных чисел установлено взаимно однозначное соответствие. Начало координат О имеет координаты 0, 0, 0. Точки оси абсцисс имеют вид (х, 0, 0), точки оси ординат—вид(0, у, 0), точки оси аппликат — вид (0,0, z). Точки координатной плоскости ху имеют вид (х, у, 0), точки координатной плоскости yz — вид (0, у, z), точки координатной плоскости xz — вид (х, 0, z). Коорди­натные плоскости разбивают все пространство на восемь трехгран­ных углов.

5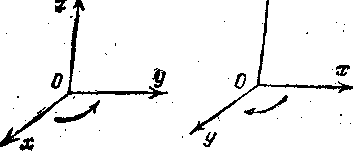 . Правая и левая системы координат в пространстве. На рис. изображены два типа взаимного расположения координатных осей в пространстве. Представим себя в роли наблюдателя, стоящего на плоскости ху с той ее стороны, в которую обращена ось z, и обращенного в сторону положительного направления оси х. Тогда в случае, изображенном на черт.1, ось у будет, идти справа налево и система координат на плоскости ху будет представляться нам как правая, а в случае, изображенном на черт, 2, ось у будет идти слева направо и система координат на плоскости ху будет представляться нам как левая. В первом случае координатную систему хуz называют правой, во втором — левой.

В случае плоскости обычно пользуются правой системой координат; при этом ocь х чертят горизонтально и поло­жительным направлением на ней считают направление слева на­право; тогда положительным направлением на оси у является направление снизу вверх. В случае пространства пользуются и той и другой системой координат; мы будем пользоваться преимущественно правой.

6. Общие декартовы; косоугольные и прямоугольные коорди­наты. Описанные координаты — как на плоскости, так и в пространстве — называются общими декартовыми координатами. Если масштабные единицы на осях совпадают с выбранной абсолютной масштабной единицей, но углы между осями — не все прямые, то получаем так называемые косоугольные координаты, которыми много пользовались в некоторых прежних курсах аналитической геометрии; мы ими пользоваться совсем не будем. Если, кроме того оси взять взаимно перпендикулярными, то получатся прямоугольные координаты, наиболее часто употребляемые в практике.

Таким образом, прямоугольными координатами называются декар­товы координаты, удовлетворяющие двум условиям: 1) координатные оси взаимно перпендикулярны и 2) масштабные единицы на осях совпадают с абсолютной единицей измерения длин. В наимено­вании этих координат прямоугольными отражено только первое из этих двух условий.

Сложение векторов

Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника

Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.

П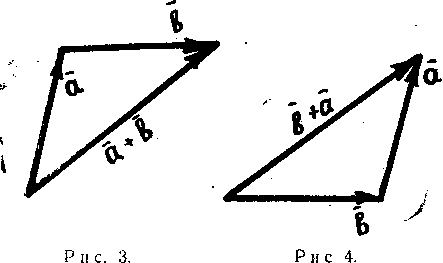 усть и — два произвольных вектора. Приложим век­тор к концу вектора , то есть совместим начало вектора с концом вектора . Тогда вектор, идущий из начала векто­ра в конец вектора называется суммой векторов и и обозначается + _. Такой способ построения суммы двух век­торов называют «правилом треугольника» (рис. ).

Если начало вектора совместить с концом вектора (рис.), то вектор, идущий из начала вектора в конец век­тора , будет вектором суммы + .

Чтобы получить вектор суммы + можно воспользо­ваться также «правилом параллелограмма». Для сложения двух векторов и по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

Как видно, сумма двух векторов обладает переместительным свойством, то есть + = + .

Понятие суммы двух векторов можно обобщить на случай любого конечного числа слагаемых. Пусть, например, даны три вектора , и с и требуется найти их сумму + + с. Искомый вектор можно получить, последовательно применяя правило треугольника:

прикладываем вектор к вектору и получаем вектор + ;

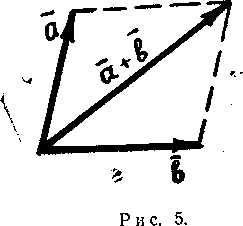в ектор ( + ) складываем с вектором и получаем искомый вектор + + (рис.5 ).

Из рис. видно, что искомый вектор суммы трех векторов можно получить, если к вектору приложить вектор , к век­тору приложить вектор и тогда вектор, идущий от начала первого вектора до конца последнего вектора будет искомым.

Это правило, называемое «правилом многоугольника», остается справедливым при нахождении суммы любого конеч­ного числа векторов. При этом сумма не зависит от порядка слагаемых.

Если при сложении нескольких векторов конец последнего вектора совпадает с началом первого вектора, то сумма рав­на нуль-вектору.

? Какой особенностью отличается многоугольник векторов, сумма которых равна нулю?

Вычитание векторов

Если даны два вектора и , то разностью — назы­вается такой третий вектор с, который в сумме с вектором составляет вектор .

И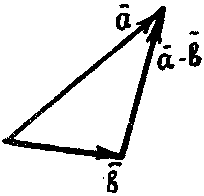 з определения суммы двух векторов вытекает правило построения вектора разности: векторы и приводят к об­щему началу и тогда вектор, идущий от конца вектора к концу вектора _, будет искомым (рис.).

Вычесть из вектора вектор означает, что к вектору надо прибавить вектор — , то есть — = + (— ).

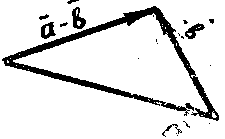На рис. к вектору приложен вектор — и, пользуясь правилом треугольника, найдена разность — .

Способ замены вычитания сложением удобен тогда, когда требуется построить алгебраическую сумму нескольких век­торов.

Умножение вектора на число

П усть дано вектор и чис­ло р. Произведением вектора на число р называется новый вектор , коллинеарный векто­ру , имеющий длину

| | = | р || | и то же самое направление, что и вектор , если р>0, и

противоположное направление, если р О, при этом = р = 0, если р = 0 или = 0.

На рис. вектор = 2 (число р = 2), а вектор =- а (число р = - ).

Противоположный вектор – можно рассматривать как результат умножения вектора на р = -1: - = (-1) .

Так, западный ветер можно представить как отрицательный восточный ветер.

Очевидно, что + (- ) = 0.

Из определения произведения вектора на число следует свойство этого произведения:

= p

Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.

Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.

Сложение коллинеарных скользящих векторов

Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы , - , расположенные на одной прямой. Прямые, на которых расположены векторы _, и _, - пересекаются. Поэтому определены векторы = ₊ и = - .

Прямые, на которых расположены векторы и пересекаются всегда, за исключением случая, когда векторы и равны по величине и противоположны по направлению, в котором говорят, что векторы _, - образуют пару (векторов).

Таким образом, под суммой векторов и можно понимать сумму векторов и и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.

Вектором можно воспользоваться для задания направления в пространстве. Так как длина вектора для этой цели безразлична, то ради удобства в этом случае можно пользоваться вектором, длина которого равна единице. Такой вектор называют ортом, или единичным вектором. В частности, ортом данной оси называется вектор длины единицы, указывающий ее направление.

Рассмотрим вектор , параллельный дан­ному орту (рис.). Легко видеть, что этот вектор можно представить в виде

= Р, (1)

где Р обозначает некоторое число (скаляр). Именно, Р = ± | |, где плюс берется, если и направлены одинаково, а минус — в противном случае. Это непосредственно вытекает из понятия произведения вектора и числа. Например, если длина вектора равна 5 и он одинаково направлен с , то

= 5 ;

Ортогональная проекция вектора на ось

1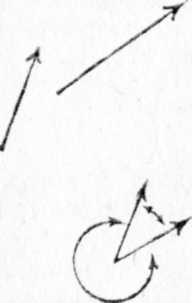 . Угол между двумя направлениями. Прежде всего условимся, что называть углом между двумя направлениями на плоскости или в пространстве. Пусть даны два направления (например, направления двух осей, или двух векторов, или вектора и оси). Проведем из произвольной точки два вектора тех же направлений (рис.). Углом между рассматриваемыми направлениями называется тот из двух углов между этими векторами, который не превосходит . Если направления одинаковы, то угол между ними равен нулю; если направле­ния противоположны, то угол между ними равен .

2. Углом между двумя векторами называется угол между их положительными направлениями, заключенный в пределах от 0 до 180°; если начала векторов не совпадают, то для измерения угла между ними следует, не изменяя направлений, перенести их так, чтобы начала совпали.