Вектора

Информационный текст

Вектор как единое, фундаментальное понятие в физике и математике

При изучении школьных курсов физики и математики встречаются с различными трактовками понятия век­тора, например такими:

вектор как направленный отрезок;

вектор как класс эквивалентных направленных отрезков;

вектор как параллельный перенос [2; 14].

Во всех этих подходах уделяется внимание лишь геометрическому подходу к векторному исчислению, рассматриваются действия над "геометрическими" векторами, что приводит к не правильному пониманию существа понятия вектора.

Рассматривается возможность формирова­ния общего понятия вектора с тем, чтобы содержание этого по­нятия включало в явном виде те физические и математические его интерпретации, с которыми придется иметь дело при дальнейшем образовании.

Для формирования такого общего представления мы ис­пользовали понятие вектора как элемента векторного пространства. Понятие векторного пространства является одним из фун­даментальных понятий современных математики и физики. На­пример, трехмерное векторное пространство является объектом изучения аналитической геометрии, векторное пространство произвольной размерности изучается в линейной алгебре. По­нятие бесконечномерного векторного пространства играет фун­даментальную роль в современном анализе, а конечномерные векторные пространства широко используются в теории функ­ций многих переменных.

Векторный аппарат широко используется в физике. Он применяется, в классической и релятивистской механике, теории поля. Понятие бесконечномерного векторного пространства иг­рает фундаментальную роль в квантовой механике. Вводя не­евклидову метрику, то есть существование таких векторов, квадрат которых меньше нуля, приходим к понятию псевдоевклидова пространства Минковского, которое применяется в спе­циальной теории относительности Эйнштейна. Если рассматривать ненулевой вектор, квадрат которого равен нулю, то придём к понятию полуевклидова пространства, которое связано с клас­сической механикой Ньютона [123; 131].

Таким образом, понятие векторного пространства широко применяется как в математике, так и в физике. Причем в прило­жениях векторного аппарата в различных областях науки ис­пользуются различные интерпретации векторного пространства.

Целесообразно обобщить знания о различных примерах векторов, которые использова­лись в физике.

Известно, что в физике рассматриваются различные виды векторов:

Свободные - такие векторы, которые можно переносить в любую точку пространства параллельно самим себе. Приме­рами таких векторов являются; вектор скорости поступательно­го движения тела, вектор ускорения, вектор момента силы, век­тор магнитной индукции постоянного магнитного поля.

Скользящие – такие векторы, которые можно переносить только по линии их действия. Их примерами являются: вектор силы, приложенной к абсолютно твёрдому телу, вектор углово­го ускорения.

Связанные - такие векторы, которые связаны с опреде­лённой точкой своего приложения. Например: вектор мгновен­ной скорости точки, вектор напряженности неоднородных элек­трических и магнитных полей.

Актуализируя знания учащихся о векторах скорости по­ступательного движения, ускорения, мгновенной скорости, си­лы, приложенной к абсолютно твердому телу, выделяем их общие свойства. В данном случае нас будут интересовать свойства сложения этих векторов и умножения на число. Особое внимание следует уде­лить свойствам сложения векторов: переместительному; сочета­тельному, существованию нулевого и противоположного векто­ра; и умножения вектора на число: сочетательному, двум рас­пределительным, умножению на единицу.

В процессе решения задач замечают, что все из­вестные векторы из курса физики обладают одинаковыми свойствами сложения и умножения на число. Целесообразно объединить выделенные свойства в таблицу. Рассмотрим на примере сил, приложенных к абсолютно твёрдому телу. и . Для определения равнодейст­вующей силы

1. Сложение: + =	2. Умножение на число: k = .
Переместительное свойство: + = + .	Псиное распределительное свойст­во: (k+n) • = k• +Mi • .
Сочетательное свойство: +( + ) = ( + )+ .	Второе распределительное свойст­во: k• ( + ) = k• +k• .
Существование нулевой си­лы : + =	Сочетательное свойство: (к • n) • =к • (n • ).
Существование для любой силы ей противоположной + (- ) = .	Умножение на единицу: 1 • = .
, , силы, приложенные к абсолютно твердому телу, к, n - числа.

Проиллюстрировать сложение векторов и умножение век­тора на число можно на следующих физических примерах.

П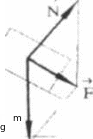 ример 1. Тело движется по наклонной плоскости под действием силы тяжести, трение отсутствует (рис.1). Результирующая сил m и , действующих на тело, равна = m + . Направление ускорения совпадает с направлением силы .

Пример 2. В физике различают умножение вектора на чис­ло и скалярную величину. В первом случае получается вектор того же смысла, во втором - новый вектор. Например, в случае умножения вектора скорости , на число 4 получаем вектор ско­рости 4 . В случае умножения вектора скорости на скаляр­ную величину массу m, получаем новую физическую векторную величину - импульс .

Пример 3. К телу в точке А при­ложена сила . Требуется найти мо­мент данной силы , вращающей тело относительно данной точки О.

Решение. Модуль момента силы равен произведению модуля силы на длину плеча: | | = | | h, где h - кратчайшее расстояние от центра вращения до линии действия силы, т.е. модуль этого вектора | | равен удвоенной площади треугольника ОАВ или произведению модуля силы на расстояние h от центра О до линии действия силы, т. е. | | = Fh.

Расстояние h называют также плечом силы.

Из рисунка непосредственно видно, что h = | |sin .

Следовательно, | | = | || |sin .

Поэтому = ,

П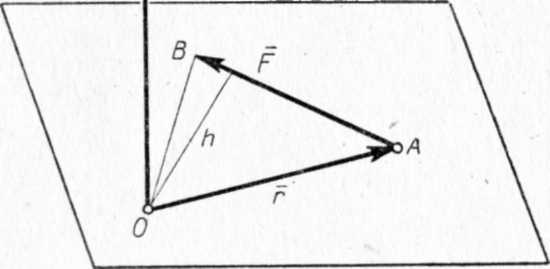 оэтому в механике принято понятие момента силы относительного центра следующим образом. Если сила (рис.) приложена к материальной точке А, то моментом силы относительно центра О называется вектор, приложенный к центру О, определяемый формулой

= ,

где = — радиус-вектор точки приложения силы .

Если сила измеряется в кГ, а плечо в м, то размер­ность вектора будет кГ• м, т. е. момент силы измеряет­ся в килограммометрах.

Полученная формула одновременно с величиной момента силы позволяет укатать направление оси вращения и направле­ние вращения самого тела. В этом ещё раз проявляется необхо­димость введения математического понятия векторного произ­ведения в курсе физики.

Ещё одним примером использования векторного произве­дения в физике является определение вектора момента импульса тела относительно точки, в частности, момента импульса планеты.

Пример 4. 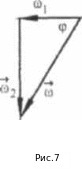Возможны два случая: шар катится ни часовой стрелке и против часовой стрелки.

В первом случае, определяя направление угловых скоро­стей по правилу правого винтa, имеем: , где

вектор полной угловой скорости.

Во втором случае 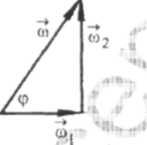аналогично: .

Следовательно, , так как в обоих случаях векторы перпендикулярны. =3,75с , = 2с , = 4,75с , Угол наклона полной угловой скорости к горизонту в первом и во втором случае одинаков и находится из векторного треугольника (рис.7 и рис.8). sin = = 0.471, 72 .

На наш взгляд, рассмотрение векторного пространства, как общего понятия физики и математики целесообразно закон­чить рассмотрением понятия векторного или силового поля, как физической интерпретации математического понятия векторно­го пространства. При таком подходе с каждой точкой поля свя­зывается вектор силы соответствующей природы. При попада­нии материальной точки в определенную точку поля дей­ствует данная сила.

В школьном курсе примеры векторных полей, например гравитационное и электростатическое, изучаются в разных классах и разных разделах, поэтому у учащихся не формируется понятие родственности данных полей. В связи с этим целесообразно рассмотреть все сило­вые поля, изученные к данному моменту на уроках физики (гравитационное, электростатическое, магнитное, электромаг­нитное), в едином блоке силовых полей, что позволит глубже раскрыть свойства из этих полей.

Сначала сравниваются гравитационное и электростатическое поля. Результат сопоставления основных харак­теристик и свойств этих полей оформляется в виде таблицы

Основные характеристики	Гравитационное поле	Электростатическое поле
Носители	Материальные тела	Заряженные тела
Сила	= G	= k
Напряженность	=	=
Потенциал	=	=

Интересно рассмотреть с учащимися связь напряженности и потенциала как однородного поля (напряженность одинакова во всех точках), и неоднородного.

Физические понятия как основа решения геометрических задач

Интересным в этом плане является знакомство с применением физических понятий к решению геометрических задач.

Подобный путь решения чисто математических проблем имел место на протяжении всей истории развития науки мате­матики. Ещё до нашей эры великий древнегреческий мыслитель Архимед обнаружил возможность доказывать новые математические факты "механическим" методом с использова­нием принципа рычага. В частности, этим способом им была установлена теорема о том, что: Три медианы треугольника пе­ресекаются в одной точке и делятся ею в отношении 2:1. При доказательстве используются следую­щие вопросы:

материальная точка;

центр масс двух материальных точек:

центр масс системы материальных точек;

свойства центра масс;

теорема Архимеда о медианах треугольника.

Теорема Архимеда

Три медианы тpeугольника имеют общую точку, и каждая из медиан делится этой точкой в отношении 2: 1, считая от вершины.

Доказательство (предложенное Архимедом).

Пусть AВC - данный треугольник. AM, CP, ВК - его ме­дианы (рис.11). Поместим в вершины треугольника равные мас­сы, например, по 1грамму. Получившаяся система трёх мате­риальных точек 1A, 1В, 1С имеет однозначно определённый центр масс в некоторой точке О (существование и единственности центра масс). В силу свойства о перегруппировке центров масс положение центра масс не изменится, если массы матери­альных точек 1B и 1С перенести в их центр масс, то есть, со­гласно правилу рычага, в точку М. Но тогда точка О окажется центром масс лишь двух материальных точек 2М и 1А. Значит. О [АМ]. Аналогично убеждаемся в том. что О [ВК] и O [CP]. Таким образом все медианы имеют общую точку О. Кроме того, по правилу рычага имеем 2 ОМ=1 ОА, или OA :ОМ = 2:1. Тео­рема доказана.

Разумеется, для того, чтобы получать математически стро­гие решения геометрических задач, все сформулированные по­ложения, апеллирующие к понятиям механики, должны быть математически обоснованы.

Пример 1. Сила = {1; 3; 2} приложена в точке В (3; 4; 5). Найти момент силы относительно точки А (1; 2; 3).

Пример 2. Момент сил, действующих на диполь. Момент сил, дейст­вующих на диполь (рис. 1.16, б) в однородном внешнем электриче­ском поле, определяется в физике, электротехнике с помощью вектор­ного произведения следующим образом:

= , | | = | || |sin ,

где = q — вектор электрического момента диполя, вектор = направлен от отрицательного к положительному заряду диполя, — вектор напряженности электрического поля. Этот момент можно записать и иначе, в соответствии с его механическим смыслом, как момент пары сил и взаимодействия точечных зарядов q и q с внешним электрическим полем = , где к = 1,2.

Вектор направлен к точке приложения силы = q , где q — заряд со своим знаком.

Сила, действующая на проводник с током в магнитном поле.

Эта сила равна = I( ) или = /c ,

где с — электродинамическая постоянная, — вектор силы тока, протекающего в проводнике, — вектор напряженности магнитного поля, в котором движется проводник, — сила, действующая на проводник длиной (направление вектора совпадает с направлением тока), — сила, действующая на проводник единичной длины (рис. 1.17).

Некоторые характеристики электромагнитных по­лей. В процессе исследования закономерностей распространения элек­тромагнитных волн в однородной изотропной среде можно с помощью векторного произведения определить такие векторные величины, как скорость распространения волны: = , где

и - векторы напряженностей соответственно электрического и магнитного полей; вектор плотности потока энергии, переносимой полем (вектор Пойнтинга): = ( ) = ,

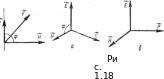
где с — скорость распространения электромагнитных волн в пустоте (рис. 1.18, б). Формула справедлива в смешанной или гауссовой систе­ме единиц.

Скорость произвольной точки вращающегося тела. Ес­ли тело вращается относительно неподвижной точки О (рис. 1.19),то в любой момент времени вектор угловой скорости вращения совпадает по направлению с мгновенной осью вращения и, проходящей через не­подвижную точку О. В этом случае линейную скорость произвольной точки М тела, расположенной вне оси и, можно определить с помощью векторного произведения векторов и : = , | |= | | | |sin .

Г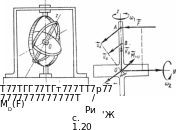 ироскопические эффекты. Гироскопом называется осесимметричное твердое тело, вращающееся относительно своей единственной неподвижной точки О, расположенной на оси симметрии (рис. 1.20, а). Вращательное движение относительно неподвижной точки можно представить в виде суммы трех независимых друг от друга движений-вращений относительно трех пересекающихся в неподвижной точке осей. Гироскоп, обладающий этими тремя движениями (тремя степе­нями свободы), называется т р е х с т е п е н н ы м или свобод н ы м. Он обладает замечательным свойством: если момент М всех внешних сил, действующих на его ротор, относительно неподвижной точки О равен нулю, то гироскоп сохраняет в пространстве положение оси собственного вращения (оси симметрии, или собственной оси).

Попытка внешними силами возбудить вынужденное движение (прецессию) собственной оси гироскопа ведет к появлению так называе­мого гироскопического момента, который определяется через векторное произведение угловых скоростей собственного и вынужденного движений:

= I ( ).

Здесь I — момент инерции ротора гироскопа относительно собствен­ной оси Oz.

Под воздействием момента внешней возмущающей силы ось ги­роскопа поворачивается, стремясь совпасть с направлением вектора момента внешних сил. При этом точка А приложения силы движется (рис. 1.20, б) не в направлении действия силы, а в направлении век­тора момента ( ) этой силы относительно неподвижной точки О.

Е сли же прецессия гироскопа ограничена или невозможна, то пара сил, соответствующая гироскопическому моменту, обусловливает дополнительные нагрузки на опоры ротора гироскопа

N = = sin

где — угол между векторами и (рис. 1.21). С этими дополнительными нагрузками нельзя не считаться, так как в ряде случаев они могут преобладать над всеми остальными.

Благодаря своему свойству сохранять положение оси в пространстве гироскоп имеет весьма многочисленные технические приме­нения.

Кроме того, очень важно, что гироскопическим эффектом обладают не только собственно гироскопы, но и все вообще быстро вращающиеся твердые тела, например роторы машин, приборов, аппаратов и других подвижных систем.

Изучение основных проблем, связанных с движением гироскопиче­ских систем, является предметом специальной науки — теории гиро­скопов. Эта наука в качестве математического аппарата широко ис­пользует простое и кратное (двойное) векторные произведения. Рас­смотрим конкретные примеры.