Нахождение скалярного произведения через координаты векторов

(3.7).

Пример 3.4. Даны координаты векторов и . Найти их скалярное произведение.

Решение. По формуле (3.7) получим: .

Приложения скалярного произведения векторов

1) Если , то угол между ними:

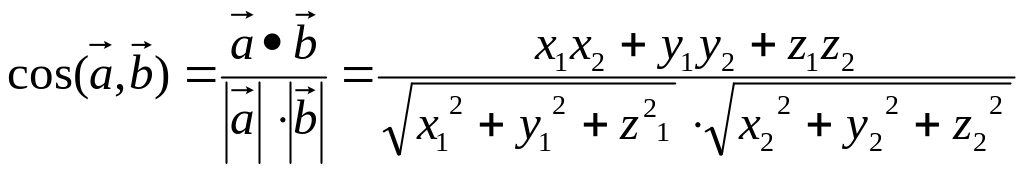(3.8).

2) (3.9).

Пример 3.5. Даны координаты векторов и . Найти косинус угла между ними.

3.5. Векторное произведение векторов

Векторным произведением двух векторов и называется третий вектор , удовлетворяющий следующим трем условиям:

1) ;

2) и ;

3) вектора образуют правую тройку (т.е. если смотреть с конца вектора , то кротчайший поворот от вектора к вектору совершается против часовой стрелки).

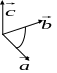
Векторное произведение обозначается: .

Свойства векторного произведения векторов:

1.	4.
2.	5.
3.

Нахождение векторного произведения через координаты векторов

Если и , то

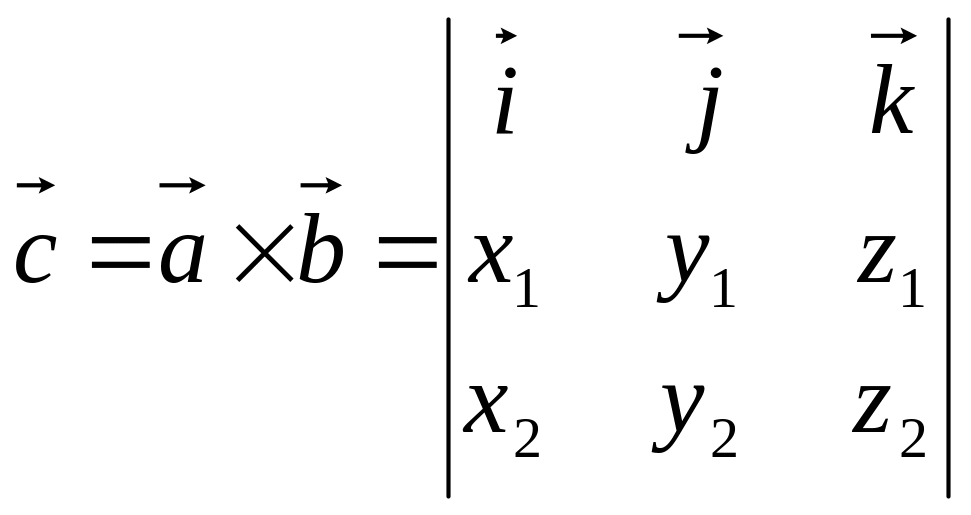(3.10).

или = (3.11).

Приложения векторного произведения векторов

1. Площадь параллелограмма построенного на векторах и :

S_парал.= (3.12).

2. Площадь треугольника построенного на векторах и :

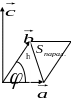
S_треуг.= (3.13).

Пример 3.6. Найти площадь параллелограмма построенного на векторах и , где , .

3.6. Смешанное произведение векторов

Смешанным произведением трёх векторов называется число равное скалярному произведению вектора на векторное произведение векторов и

Смешанное произведение обозначается и по определению равно:

_(3.14).

Свойства смешанного произведения векторов:

1 . ;

2. ;

3. ;

4. ;

5. (не нарушается круговой порядок);

6. (нарушается круговой порядок).

Нахождение смешанного произведения через координаты векторов

Если то

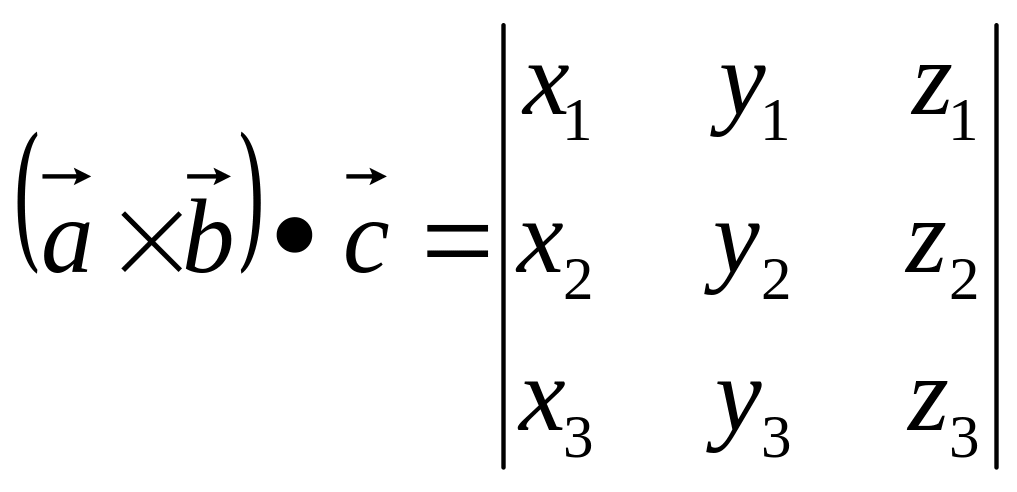(3.15).

Приложения смешанного произведения векторов

1. Объем параллелепипеда построенного на векторах :

V_парал. = (3.16).

2. Объем пирамиды построенной на векторах :

V_пир. = (3.17).

3. Признак компланарности трех векторов (линейной зависимости трех векторов): если 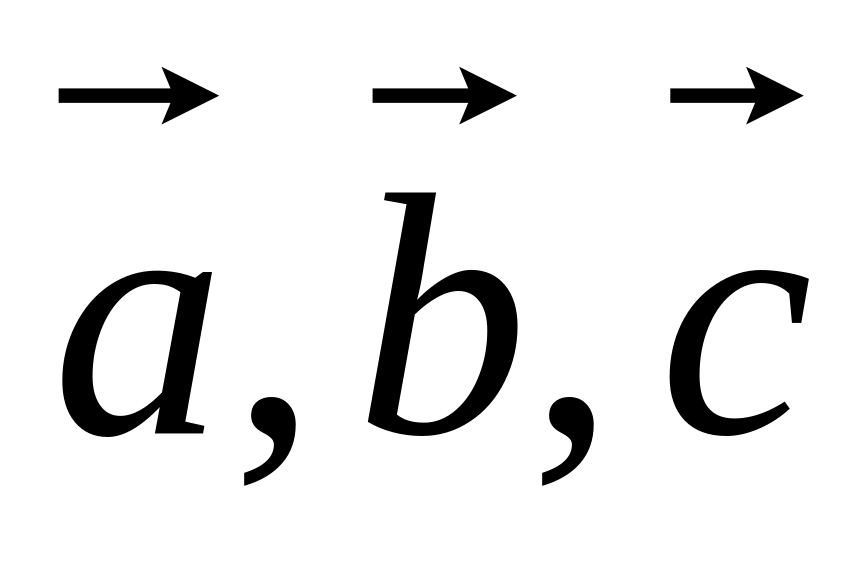компланарны (линейно зависимы),

или 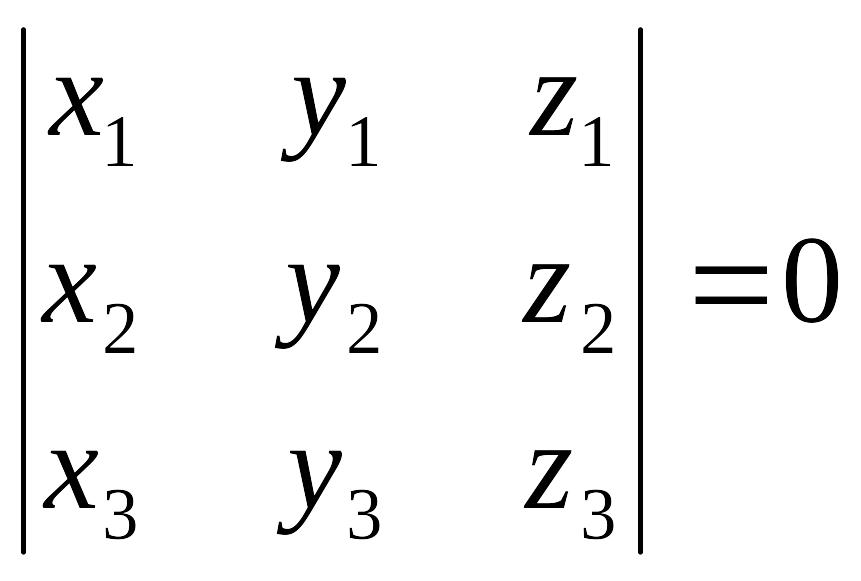(3.18).

Примеры решения задач

Пример 1. Дано: ве 3 рамма построенного на векторах векторовнечной точек: 00000000000000000000000000000000000000000000000000000 , , .

Вычислить: а) ; б) ; в) .

Решение.

а) ;

б) с учетом свойств скалярного произведения имеем:

Пример 2. Даны векторы = (2; –1; – 2) и = (8; – 4; 0).

Найти: а) векторы = 2 и = – ; б) длины векторов и ; в) скалярный квадрат вектора ; г) скалярное произведение векторов и ; д) угол между векторами и .

Решение. а) По определению =2, =(4;–2;–4); = – =(6;–3;2).

б) Найдем длины векторов и :

.

в) Скалярный квадрат равен квадрату модуля вектора, т.е.

.

г) По формуле (3.7) скалярное произведение векторов и равно:

.

д) По формуле(3.8) найдем косинус угла между векторами и :

.

Тогда угол между векторами и равен:

.

Пример 3. Найти внутренний угол при вершине A в треугольнике с вершинами A(1; 2; –1), B(5; 5; 4) и C(13; 18; 20).

Решение. Найдем координаты векторов и .

, . По формуле (3.8) имеем

.

Таким образом, .

Пример 4. Найти длину вектора , перпендикулярного векторам и .

Решение. Искомый вектор . По формуле (3.10) находим:

.

! Проверьте самостоятельно вычисление определителей.

Отсюда .

Пример 5. Найти площадь треугольника с вершинами A(2;2;2), B(1;3;3), C(3;4;2).

Решение. .

, .

.

! Проверьте самостоятельно вычисление определителя.

(кв. ед.).

Пример 6. Доказать компланарность векторов , , .

Решение. По формуле (3.15) находим смешанное произведение :

.

! Проверьте самостоятельно вычисление определителей.

=0, а это значит, что векторы компланарны.

Пример 7. Найти объем тетраэдра с вершинами в точках A(–1;1;0), B(2;–2;1); C(3;1;–1); D(1;0;–2).

Решение. Рассмотрим векторы , , .

Искомый объем тетраэдра равен объема параллелепипеда, построенного на векторах , и . По формуле (3.17):

.

! Проверьте самостоятельно вычисление определителя.

(куб. ед.).

Пример 8. Найти объем параллелепипеда построенного на векторах , где , , .

Решение. Найдем смешанное произведение векторов по формуле (3.15):

.

Искомый объем параллелепипеда, построенного на векторах , и по формуле равен:

(куб. ед.).

Пример 9. Пусть в магазине имеется набор из 5 товаров, количество и стоимость (в тыс. руб.) которых указана в таблице

Товар	1	2	3	4	5
Количество	50	150	75	100	200
Стоимость	35	40	70	80	20

Требуется определить общую стоимость товара в магазине.

Решение. Введём в рассмотрение вектор , координатами которого являются количество i – го товара (i = 1,2,3,4,5) и вектор , образованный из цен на эти товары. Тогда искомую общую стоимость S можно найти по формуле

Пример 10. На предприятии имеется шесть цехов. Плановые задания цехов (в млн. руб.) образуют вектор план

Предположим, что к какому-то моменту цехи выполнили свои планы соответственно на 20%,40%.50%,70%,30%,10%.Определить стоимость S произведенной предприятием продукции на данный момент.

Решение.

Если ввести в рассмотрение вектор выполнения плана, то имеем