
- •Учебно-методический комплекс
- •Специальность
- •210300.62 - Радиотехника
- •3.5. Методические указания к выполнению лабораторных работ Общие указания
- •Охрана труда и тб
- •Библиографический список
- •Лабораторная работа 1
- •3. Описание лабораторной установки
- •4. Порядок выполнения работы
- •5. Содержание отчета
- •Лабораторная работа 2 исследование дифференцирующей и интегрирующей цепей
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Описание лабораторной установки
- •4. Порядок выполнения работы
- •Лабораторная работа 3 исследование функций распределения и плотностей вероятности значений случайных сигналов
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Описание лабораторной установки
- •4. Методика выполнения работы
- •5. Содержание отчета
- •Лабораторная работа 4 исследование характеристик частотно-избирательных цепей на основе колебательных контуров
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Описание лабораторной установки
- •4. Методика выполнения работы
- •Лабораторная работа 5
- •3. Описание лабораторной установки
- •4. Порядок выполнения работы
- •5. Содержание отчета
- •Лабораторная работа 6 исследование прохождения частотно-модулированных колебаний через колебательный контур
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Описание лабораторной установки
- •4. Порядок выполнения работы
- •5. Содержание отчета
- •Лабораторная работа 7 синтез сигналов по дискретным отсчетам котельникова
- •2. Основные теоретические положения
- •3. Описание лабораторной установки
- •4. Методика выполнения работы
- •5. Содержание отчета
- •Лабораторная работа 8 радиотехнические устройства с обратной связью
- •1. Цель работы
- •2. Основные теоретические положения
- •Примеры радиотехнических устройств с обратной связью
- •3. Описание лабораторной установки
- •4. Методика выполнения работы
- •5. Содержание отчета
- •Лабораторная работа 9 нелинейное резонансное усиление и умножение частоты
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Описание лабораторной установки
- •4. Методика выполнения работы
- •5. Содержание отчета
- •Лабораторная работа 10 амплитудная модуляция
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Описание лабораторной установки
- •4. Методика выполнения работы
- •5. Содержание отчета
- •Лабораторная работа 11 детектирование амплитудно-модулированного сигнала
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Описание лабораторной установки
- •4. Методика выполнения работы
- •5. Содержание отчета
- •Лабораторная работа 12 исследование автогенератора гармонических колебаний
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Описание лабораторной установки
- •4. Методика выполнения работы
- •5. Содержание отчета
- •3.6. Методические указания к выполнению практических занятий
- •Практическое занятие № 1 Определение спектральной плотности для различных сигналов
- •Практическое занятие № 2 Определение корреляционных функций для детерминированных сигналов
- •Практическое занятие № 3 Определение параметров ам- сигналов
- •Практическое занятие № 4 Синтезирование фильтров низкой частоты с помощью активных цепей
- •Содержание
- •Малинин Сергей Иванович Токарев Владимир Семенович радиотехнические цепи и сигналы
- •191186, Санкт-Петербург, ул. Миллионная, д. 5
5. Содержание отчета
Отчет по работе должен включать в себя следующее:
1. Результаты определения масштабов графиков согласно п. 2;
2. Графики функций распределения и плотностей вероятностей значений сигналов, исследованных в п. 3;
3. Анализ соответствия графиков, полученных в п. 3, теоретическим результатам (выражения (3.3)–(3.7)) [4];
4. Графики функций распределения для последовательных сумм синусоидальных и треугольных сигналов согласно п. 4;
5. Вывод о скорости сходимости распределения вероятности суммы независимых случайных сигналов к гауссовскому закону.
Литература: [1], с. 149-156; [2], с. 165-169
Лабораторная работа 4 исследование характеристик частотно-избирательных цепей на основе колебательных контуров
1. Цель работы
Изучение
частотно-избирательных цепей на основе
колебательных контуров. Последовательный
и параллельный колебательные контуры
часто используются в качестве основного
элемента линейных частотно-избирательных
цепей (фильтров, резонансных усилителей
и т. п.).
К основным
характеристикам линейных цепей относятся
импульсная характеристика h(t)
и комплексный
коэффициент передачи (частотная
характеристика)
![]() .
В исследуемых цепях вид этих характеристик
полностью определяется резонансной
частотой
.
В исследуемых цепях вид этих характеристик
полностью определяется резонансной
частотой
![]() и добротностью Q
контуров, а связь между ними —
преобразованиями Фурье.
и добротностью Q
контуров, а связь между ними —
преобразованиями Фурье.
Исследуются временные и частотные характеристики колебательных контуров, влияние на них активных потерь, взаимосвязь временных и частотных параметров контуров.
2. Основные теоретические положения
Последовательный
колебательный контур
(рис. 4.1, а)
удобно рассматривать как четырехполюсник.
На резонансной частоте
он обладает низким входным сопротивлением
и для обеспечения колебательного режима
должен подключаться к источнику сигнала
с достаточно малым выходным сопротивлением
![]() таким, чтобы выполнялось условие
таким, чтобы выполнялось условие
![]() ,
где
,
где
![]() —
волновое, или характеристическое,
сопротивление контура.
—
волновое, или характеристическое,
сопротивление контура.


а б Рис. 4.1
Пренебрегая
сопротивлением нагрузки (полагая его
достаточно большим,
![]() >> r),
запишем дифференциальное уравнение
для выходного напряжения четырехполюсника
>> r),
запишем дифференциальное уравнение
для выходного напряжения четырехполюсника
![]() :
:
 , (4.1)
, (4.1)
где в качестве
входного воздействия взята взвешенная
функция включения
![]() (функция Хевисайда). Однородному
дифференциальному уравнению
(функция Хевисайда). Однородному
дифференциальному уравнению
 (4.2)
(4.2)
соответствует характеристическое уравнение
![]()
с корнями
![]() ;
здесь a = r/(2L),
;
здесь a = r/(2L),
![]() («собственная» резонансная частота
контура). Решение неоднородного
дифференциального уравнения (4.1) ищут
в виде суммы решения однородного
уравнения (4.2) и так называемого частного
решения уравнения (4.1), которое при
выбранном входном воздействии оказывается
просто константой U:
(«собственная» резонансная частота
контура). Решение неоднородного
дифференциального уравнения (4.1) ищут
в виде суммы решения однородного
уравнения (4.2) и так называемого частного
решения уравнения (4.1), которое при
выбранном входном воздействии оказывается
просто константой U:
![]() .
.
Используя
очевидные начальные условия
![]() ,
i(0) = 0,
находят константы
,
i(0) = 0,
находят константы
![]() и
и
![]() и записывают решение:
и записывают решение:
 ,
,
которое при нормировке к U = 1 В становится безразмерной переходной характеристикой четырехполюсника g(t). Так как импульсная характеристика h(t) = dg/dt, получают

![]() ,
t ³ 0. (4.3)
,
t ³ 0. (4.3)
График
h(t)
приведен на рис. 4.1, б.
В выражении (4.3) приближение сделано в
предположении малых потерь α и ωр=ω0,
а также введена постоянная времени
![]() последовательного колебательного
контура. Здесь
последовательного колебательного
контура. Здесь
![]() —
нагруженная добротность контура,
определяемая соотношением
—
нагруженная добротность контура,
определяемая соотношением
![]() . (4.4)
. (4.4)
Комплексный коэффициент передачи последовательного колебательного контура в так называемом приближении малых расстроек рассчитывается просто:
 =
=

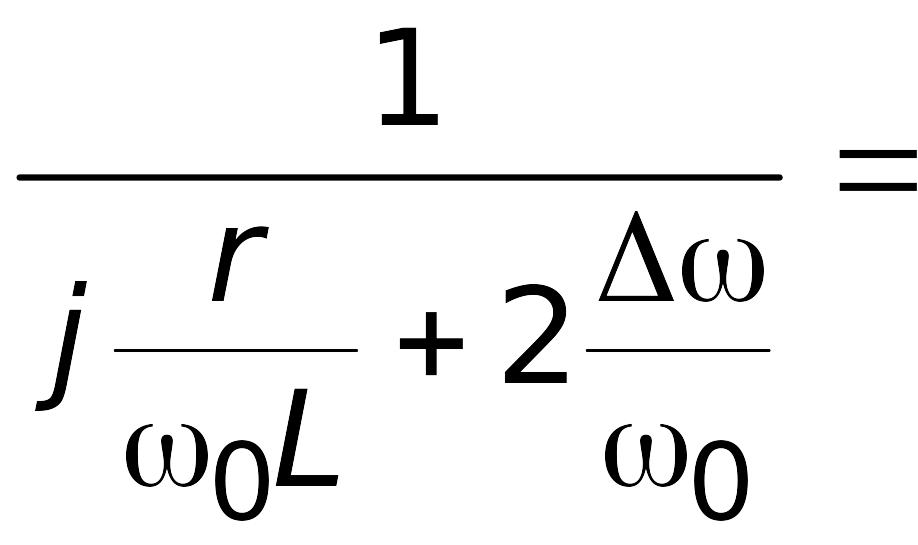
=

 . (4.5)
. (4.5)
Здесь принято
![]() ,
,
![]() —
в приближении малых расстроек.
—
в приближении малых расстроек.
Комплексный коэффициент передачи может быть также получен в результате применения к импульсной характеристике h(t) прямого преобразования Фурье:
 . (4.6)
. (4.6)
Нижним пределом интеграла в выражении (4.6) берут 0, так как импульсная характеристика физически реализуемого четырехполюсника существует только при t ³ 0. С использованием введенной постоянной времени результат (4.5) записывается в виде
 .
.
АЧХ и ФЧХ цепи определяются выражениями
 ,
,
![]() . (4.7)
. (4.7)
Входное
сопротивление последовательного
колебательного контура на резонансной
частоте мало и равно эквивалентному
сопротивлению потерь,
![]() = r.
Поэтому последовательные контуры часто
используют как режекторные
фильтры для подавления сигнала на
резонансной частоте.
= r.
Поэтому последовательные контуры часто
используют как режекторные
фильтры для подавления сигнала на
резонансной частоте.
Параллельный
колебательный контур
представляет собой параллельное
соединение L
и C
элементов (рис. 4.2, а). Используют
высокодобротные катушки индуктивности
и конденсаторы с малыми потерями, причем
потерями в конденсаторе в большинстве
случаев пренебрегают и собственные
потери контура представляют сопротивлением
![]() ,
отнесенным к индуктивности. Для удобства
анализа схемы последовательное соединение
и L
пересчитывают в параллельное соединение
эквивалентного
сопротивления
,
отнесенным к индуктивности. Для удобства
анализа схемы последовательное соединение
и L
пересчитывают в параллельное соединение
эквивалентного
сопротивления
![]() и L,
пренебрегая квадратом сопротивления
потерь
и L,
пренебрегая квадратом сопротивления
потерь
![]() по сравнению с квадратом индуктивного
сопротивления, (
по сравнению с квадратом индуктивного
сопротивления, (![]() L)2
>>
.
На резонансной частоте параллельный
контур имеет достаточно высокое
эквивалентное
сопротивление
L)2
>>
.
На резонансной частоте параллельный
контур имеет достаточно высокое
эквивалентное
сопротивление
![]() ,
где r,
как и для последовательного контура, —
волновое, или характеристическое,
сопротивление,
равное сопротивлению одной ветви контура
на резонансной частоте,
,
где r,
как и для последовательного контура, —
волновое, или характеристическое,
сопротивление,
равное сопротивлению одной ветви контура
на резонансной частоте,
![]() ;
;
![]() —
собственная
(ненагруженная) добротность
колебательной системы. Для сохранения
в контуре колебательного режима
добротность должна быть достаточно
велика, следовательно, подключаемые к
нему сопротивления источника сигнала
(генератора)
—
собственная
(ненагруженная) добротность
колебательной системы. Для сохранения
в контуре колебательного режима
добротность должна быть достаточно
велика, следовательно, подключаемые к
нему сопротивления источника сигнала
(генератора)
![]() и нагрузки
должны быть большими (
,
³
и нагрузки
должны быть большими (
,
³ ![]() ).
).


а б Рис. 4.2
Для
исследования временных характеристик
параллельного контура источник напряжения
u(t)
(рис. 4.2, а) заменяют источником
тока
![]() ,
а параллельно подключенные к контуру
сопротивления
и
пересчитывают с учетом
в эквивалентное сопротивление
,
а параллельно подключенные к контуру
сопротивления
и
пересчитывают с учетом
в эквивалентное сопротивление
![]() (рис. 4.2, б) в соответствии с равенством
(рис. 4.2, б) в соответствии с равенством
 ,
где
,
где
![]() ,
—
нагруженная
добротность
параллельного контура. Иногда используют
понятие внешней
добротности
,
—
нагруженная
добротность
параллельного контура. Иногда используют
понятие внешней
добротности
![]() ,
которая связывает собственную и
нагруженную добротности
,
которая связывает собственную и
нагруженную добротности
 .
.
Импульсной
реакцией,
или импульсной
характеристикой,
параллельного колебательного контура
принято называть напряжение
при воздействии на контур дельта-импульса
тока
![]() (при экспериментальном определении
импульсной характеристики используют
достаточно короткий импульс). Импульсная
реакция
параллельного контура имеет колебательный
характер и может быть записана как
(при экспериментальном определении
импульсной характеристики используют
достаточно короткий импульс). Импульсная
реакция
параллельного контура имеет колебательный
характер и может быть записана как

 . (4.8)
. (4.8)
Здесь
![]() .
Приближение (4.8) с учетом того, что α -
мало и ωр≈ω0 (напомним, что
.
Приближение (4.8) с учетом того, что α -
мало и ωр≈ω0 (напомним, что
![]() ,
где
,
где
![]() —
«собственная» резонансная частота
контура), принимают для высокодобротного
контура. Вводят также понятие постоянной
времени
—
«собственная» резонансная частота
контура), принимают для высокодобротного
контура. Вводят также понятие постоянной
времени
![]() нагруженного параллельного контура и
записывают выражение (4.8) в форме
нагруженного параллельного контура и
записывают выражение (4.8) в форме
 ,
,
![]() . (4.9)
. (4.9)
Из
выражений (4.3) и (4.9) следует, что
![]() является интервалом
времени между точками, соответствующими
спаду огибающей импульсной характеристики
в e
= 2,72… (основание натуральных логарифмов)
раз.
является интервалом
времени между точками, соответствующими
спаду огибающей импульсной характеристики
в e
= 2,72… (основание натуральных логарифмов)
раз.


а б Рис. 4.3
Из
выражения (4.6) следует, что при безразмерном
размерностью h(t)
является 1/с.
При определении импульсной характеристики
параллельного колебательного контура
было принято воздействие в виде
дельта-импульса тока, а в качестве
реакции —
напряжение на контуре, поэтому размерностью
здесь будет Ом —
размерность отношения
![]() , —
а размерностью
h(t)
будет Ом/с = 1/Ф,
что поясняет присутствие в выражениях
(4.8) и (4.9) множителя 1/С.
Комплексный коэффициент передачи
параллельного колебательного контура
записывается как
, —
а размерностью
h(t)
будет Ом/с = 1/Ф,
что поясняет присутствие в выражениях
(4.8) и (4.9) множителя 1/С.
Комплексный коэффициент передачи
параллельного колебательного контура
записывается как
 , (4.10)
, (4.10)
где
![]() —
абсолютная расстройка, как и для
последовательного колебательного
контура. Можно показать, что если
—
абсолютная расстройка, как и для
последовательного колебательного
контура. Можно показать, что если
![]() —
полоса заграждения контура на уровне
0,707 от максимума АЧХ, то
—
полоса заграждения контура на уровне
0,707 от максимума АЧХ, то
![]() —
добротность контура, практически
совпадающая с нагруженной добротностью
контура, определенной через временные
характеристики. Из выражения (4.10)
определяют АЧХ и ФЧХ цепи (рис. 4.3, б):
—
добротность контура, практически
совпадающая с нагруженной добротностью
контура, определенной через временные
характеристики. Из выражения (4.10)
определяют АЧХ и ФЧХ цепи (рис. 4.3, б):
 ,
,
![]() . (4.11)
. (4.11)
Рис. 4.4
 ,
,
 .
.
При
подключении источника напряжения u(t)
к части индуктивной ветви контура он
может быть заменен генератором тока
 ,
подключенным к контуру вида
рис. 4.2, б. В этом случае комплексная
частотная характеристика приобретает
вид
,
подключенным к контуру вида
рис. 4.2, б. В этом случае комплексная
частотная характеристика приобретает
вид
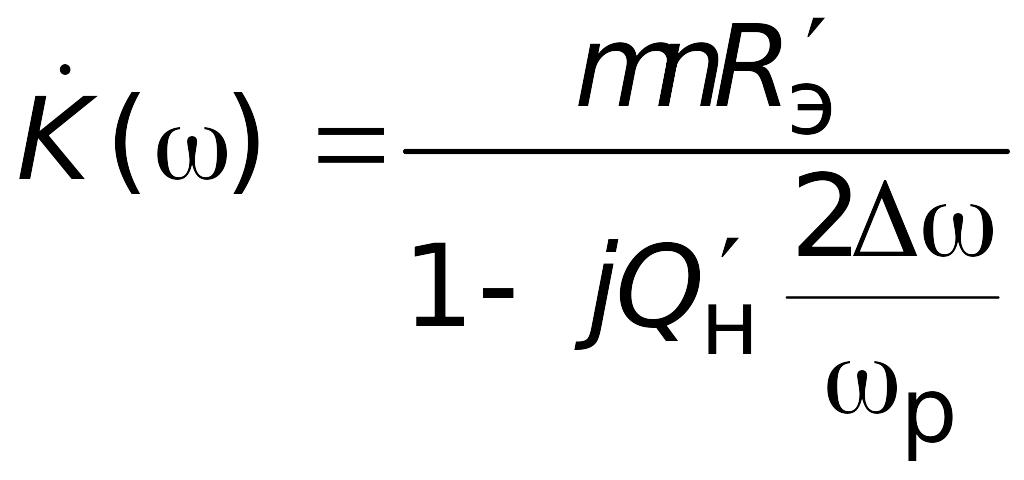 ,
,
где
 —
эквивалентная нагруженная добротность,
—
эквивалентная нагруженная добротность,
 —
эквивалентное сопротивление контура
с учетом собственных и внешних потерь,
—
эквивалентное сопротивление контура
с учетом собственных и внешних потерь,
 —
собственные потери контура (от
коэффициентов включения не зависят),
—
собственные потери контура (от
коэффициентов включения не зависят),
 ,
,
 —
пересчитанные с учетом частичного
включения сопротивления генератора и
нагрузки. Подбором коэффициентов
включения удается обеспечить требуемую
полосу пропускания контура и расчетное
эквивалентное сопротивление. Это
особенно важно при использовании
параллельного контура в качестве
нагрузки в резонансных усилителях и
генераторах.
—
пересчитанные с учетом частичного
включения сопротивления генератора и
нагрузки. Подбором коэффициентов
включения удается обеспечить требуемую
полосу пропускания контура и расчетное
эквивалентное сопротивление. Это
особенно важно при использовании
параллельного контура в качестве
нагрузки в резонансных усилителях и
генераторах.
