2.2. Функции распределения.

В Маткаде эти законы строятся с помощью встроенных функций распределений:

pnorm(x,m,σ) - интегральный нормальный закон распределения с математическим ожиданием m и среднеквадратичным отклонением σ;

punif(x,a,b) – интегральный равномерный закон распределения в пределах а и b.

pchisq(x,d) – интегральный закон распределения хи – квадрат с “d” степенями свободы;

pF(x,d1,d2) – интегральный закон распределения Фишера со степенями свободы “d1”и”d2”.

pt(x,d) – интегральный закон распределения Стьюдента со степенью свободы “d”.

Пример 7. Построить функцию распределения для нормального закона с математическим ожиданием m=5 и среднеквадратическим отклонением σ =2.

Построение функции приведено на Рис. 9.

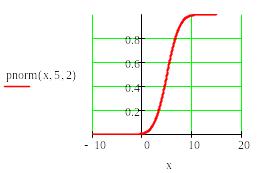
Рис. 9. Построение интегральной функции нормального закона.

Пример 8. Построить функции распределения для распределений хи- квадрат, Фишера и Стьюдента.

Соответствующие функции построены на Рис. 10-13.

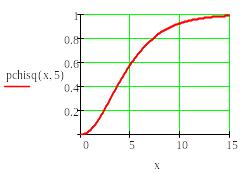
Рис. 10. Построение интегрального закона Рис. 11. Функция распределения хи- квадрат.

равномерного распределения.

.

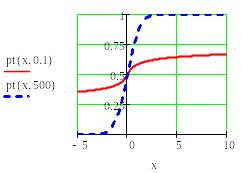
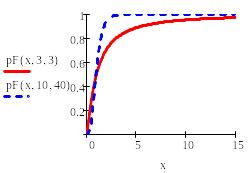
Рис. 12. Функция распределения Фишера. Рис. 13. Функция распределения Стьюдента.

2.3. Построение гистограмм.

Представление об эмпирической функции распределения можно составить по гистограммам. Последние создаются на основе векторов выборок с помощью процедур hist(i,v) и histogram(). Аргументы у обеих процедур одинаковы: первый определяет интервалы для создания гистограммы, а второй — это собственно выборка, на основе которой строится гистограмма. Что касается первого аргумента, то он может быть либо вектором конечных точек интер­валов для группировки данных выборки, либо целым числом, задающим чис­ло интервалов. В последнем случае весь диапазон значений в выборке разби­вается на равные интервалы.

Разница между процедурами hist () и histogram() состоит в том, что первой возвращается вектор частот, с которыми данные выборки попадают в базо­вые интервалы гистограммы. Второй процедурой возвращается матрица. Первый ее столбец содержит срединные точки базовых интервалов, а вто­рой — частоты попадания данных в эти интервалы.

Пример 9. По заданным реализациям случайной величины Х построить ее гистограмму.

Произведено 500 наблюдений. Результаты наблюдений сведены в статистический ряд:

Интервалы Наблюдений	-4-;3	-3;-2	-2;-1	-1;0	00;1	11;2	22;3	33;4
Число наблюдений в данном интервале	е6	225	772	1133	1120	888	446	110
Частота m/n	00.012	00.05	00.144	00.266	00.240	00.176	00.092	00.02

Требуется построить гистограмму этого ряда. Гистограмма реализуется в Маткаде с помощью нескольких функций. Так как нам уже заданы частоты попадания случайной величины в каждый интервал, то мы построим ее следующим образом:

1. Сформируем векторы интервалов наблюдений v и частот f.

2. Используя функцию Histogram, найдем центры каждого интервала.

3. Построим плоский график, введя по оси абсцисс первый столбец матрицы Н, а по оси ординат – вектор f.

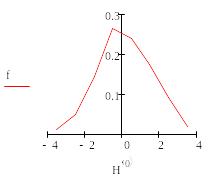
В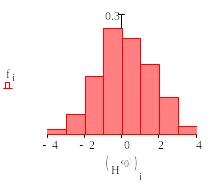 ызовем на панели форматирования (Formating Currently Selected X-Y Plot) окно Traces (следы) и в столбце Тип выберем строку Solid Bar.Получим график гистограммы, показанной ниже.