2.1 Технологія дослідження структури та визначення параметрів транспортних потоків. Перевірка гіпотези щодо структури транспортних потоків

Дослідження динамічної системи проведемо на прикладі залізничної станції. Вхідним потоком та потоком обслуговування в даній системі є поїздопотоки. Розглянемо процедуру дослідження структури та визначення параметрів вхідного поїздопотоку. Технологія досліджень передбачає використання функції розподілу безперервної випадкової величини (ВВ), яка являє собою інтервали часу між двома послідовними надходженнями вимог (поїздів) до системи (станції).

Порядок дослідження такий:

а) спочатку збирають вихідний статистичний матеріал про інтервали часу між надходженням двох составів на станцію, які можна упорядкувати в одномірний масив {t_i}, де і = 1, n. Для більшої правильності результатів обсяг вибірки повинен бути значним, тобто n  100;

б) визначають розмах варіювання ВВ t_i, тобто мінімальне та максимальне значення масиву;

в) знаходять оптимальне число інтервалів розбиття, тобто інтервал від t_min до t_mах розбивають на часткові інтервали, кількість яких дорівнює цілій частині

k = 1+3.33  lg n; (2.1)

г) оцінюють довжину часткового інтервалу

 = (t_min - t_mах)  k; (2.2)

д) кінці часткових інтервалів складають масив {b_j}, де j=1,k+1;

ж) емпірична частота попадань ВВ t_i у кожний j- ий інтервал складає масив {M_j} при умові, що b_j  t_i  b_j+1, тобто t_ib_j;b_{j + 1};

к) визначають емпіричну частість {f_j}

f_j = M_j / n; (2.3)

л) будують гістограму емпіричних частот M_j та частостей f_j, після чого висувають гіпотезу про вигляд вхідного потоку. Як показали попередні дослідження, найчастіше вхідний поїздопотік підпорядкований експоненційному закону розподілу зі щільністю

(2.4)

та функцією розподілу:

(2.5)

де - інтенсивність потоку, тобто середня кількість подій, що приходиться на одиницю часу;

t – поточне значення величини, що досліджується.

, (2.6)

де - математичне очікування випадкової величини, .

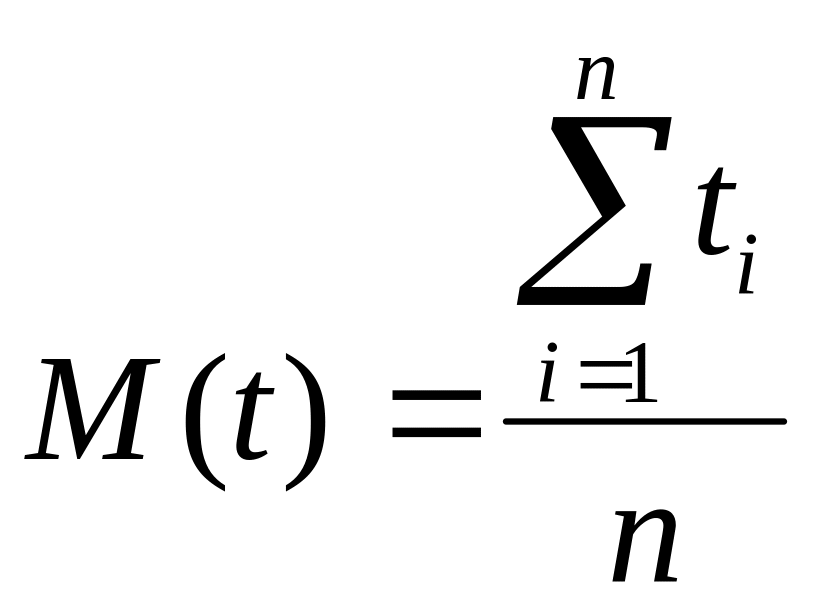Тобто вхідний поїздопоток на станцію є найпростішим;

м) перевіряють гіпотезу, яку було висунуто. Найбільш потужним критерієм для перевірки гіпотез є критерії узгодженості ² Пірсона. Для його оцінювання складається таблиця.

Таблиця 2.1 – Перевірка гіпотези за критерієм Пірсона

Статья I.Інтервал bj– bj+1	Емпірична		Теоретична
	частота	частість	Раздел I.1частість	частота
	Mj	fj	fj т =е-bj- е-bj+1	Mтj =Fтj n
…	…	…	…	…	…

Суму необхідно порівняти з критичним значенням ²_крит, яке визначається за таблицями при заданому рівні значення  = 0,05 та кількості ступенів свободи , що дорівнює кількості інтервалів розбиття гістограми за винятком кількості параметрів, що оцінюються, та одиниці на похибку експериментатора.

Якщо , то потік є найпростішим, тобто він підпорядкований експоненційному закону. При невиконанні умови вхідний потік треба перевірити на відповідність потоку Ерланга 2-ого або 3-ого порядку (К=2, К=3).

Таким чином визначається структура і оцінюється параметр  вхідного поїздопотоку та перевіряється гіпотеза щодо його розподілу.

Для визначення структури і параметрів розподілу потоку обслуговування вихідними даними є масив випадкової величини часу обслуговування поїздів на станції. Процедура дослідження потоку обслуговування аналогічна процедурі дослідження вхідного потоку.