6. Логарифмическая производная. Найти производную функции

Пример 6.1. Найти производную функции

►. Предлагаемая функция не относится к классу Тем не менее прием логарифмической производной позволяет более оптимально получить результат.

lny = 1/2(lnx + ln|x – 1 – ln|x – 2|) 

(lny)` = y`/y = 1/2(1/x + 1/(x – 1) – 1/(x–2)).

Пользуясь тем, что (lny)` = y`/y получаем

y` = (lny)`y = .◄

Пример 6.2. Найти производную степенно-показательной функции

y = .

► Логарифмируя, получим (так как 1 + 1/x > 0)

lny = xln(1 + 1/x)

Отсюда находим производные левой и правой частей

(lny)` = y`/y = ln(1 + 1/x) – 1/(1 + x).

Следовательно,

y` = (lny)`y = .◄

1) ((sin(2x))^11x) 2) ((cos(3x))log₃^(2x))

3) ((sin(7x))^ctg(23x)) 4) ((arctg(8x))^x(45x))

5) ((arcsin(9x))^(5x)) 6) ((arccos(7x))^ln(56x))

7) ((log₃₇(3x))^arccos(55x)) 8) ((log₅₅(5x))^arcsin(56x))

9) ((sin(2x))^arccos(59x)) 10) ((cos(8x))^arcctg(803x))

11) ((tg(12x))^arctg(172x)) 12) ((log₃₃(22x))^tg(11x))

13) ((log₈(23x))^cosec(9x)) 14) ((log₅(16x))^sec(8x))

15) ((log₃(51x))^sin(4x)) 16) (log₃₄x³ln31x)

17) (85ln(x²+2x+17)) 18) (89log₃₇(ax+b))

19) (62ln(e^x+x⁴)) 20) (92log(arccos²x))

21) (77e3^12x) 22) (11x^sinx)

23) (999(arcsinx)^5x) 24) (logx)^logx

25) (17sinx)^arcsinx 26) (65cos51x)^arcctgx

27) ((9tgx)^2sinx) 28) ((91thx)^shx)

29) (7earccosx²lnx) 30) (log³⁴x)^lnx

7. Неявные функции

Пример 7.1. Уравнение x² + y² = 1 неявно определяет на интервале (-1,1) две функции:

y₁(x) = ,

y₂(x) = .

Найти их производные, не используя явных выражений.

►Пусть y(x) - любая из этих функций. Тогда, дифференцируя по x тождество

x² + y²(x) = 1,

получим

2x + 2y(x)y`(x) = 0.

Отсюда

y`(x) = –x/y(x),

т. е.

y`1(x) = –x/y1(x) = – , y`2(x) = – .◄

Пример 7.2. Уравнение arctg(y/x) = ln задаёт неявную функцию. Найти ее производную.

► Продифференцировав равенство arctg(y/x) = ln получим

,

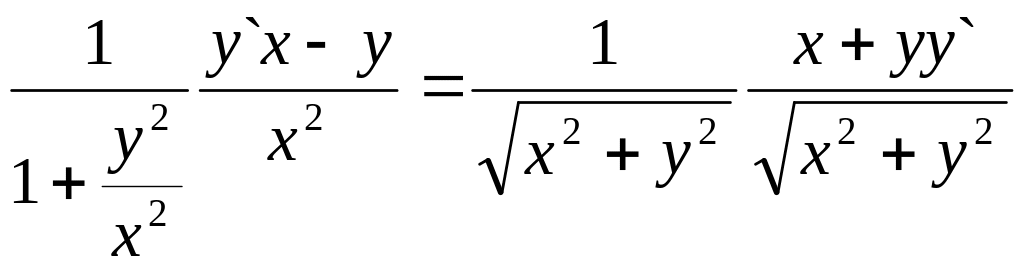откуда

y` = (xy).◄

Найти производную неяной функции y = f(x), определяемой уравнением

1) sin(xy) + 2x = 3^xy 2) cos(xy)+2^x = 5^xy

3) tg(xy) + 5^x = 8^xy 4) arccos(x²y) + log₂x = 11^xy

5) cos(xy⁴) + arcsin(23x³) = 22^xy 6) sin(xy) + 2x = 3^xy

7) x³ + y⁴ = xy 8) 5x⁷ + y⁸ = x⁸y8

9) 5x⁶ + y⁹ = xy9 10) 8x⁹ + y⁷ = x⁷y²

11) 4x⁶ + y³ = x⁵y² 12) log₅(xy³) + arcsin(9x⁵) = 19^xy

13) log₈(xy⁸) + arcsin(4x⁷) = 18^xy 14) log₉(xy⁹) + arcsin(2x⁹) = 1995^xy

15) log₂(xy⁴) + arcsin(3x³) = 19^{xy 16) x2 + 2xy – y2 = 2x}

^{17) y2 = 2px 18)} = 1

19) 20)

21) arctg = ln 22) x³ – 2x²y² + 5x + y – 5 = 0

23) e^xy + xy = e 24) 2ylny = x

25) e^xsiny – e^ycosx = 0 26) sin(xy) + cos(xy) = 0

27) 2^x+2^y = 2^x+y 28) x – y = arcsinx – arcsiny

29) x^y = y^x 30)

8. Найти производную функции заданной параметрически

Пример 8.1. Найти y`_x если, x = cos²t, y = sint, t(0,/2).

► Воспользовавшись формулой : (y`<sub>x</sub> = y`_t/x`_t) получим

x`<sub>t</sub> = –2costsint, y`_t = cost, y`_x = – 1/2sint◄

Пример 8.2. Найти y`_x если, x = acos³t, y = bsin³t, t(0,/2)

► Функции x(t) и y(t) дифференцируемы при всех t, и x`_t = –3acos²t·sint  0 на интервале (0,/2). Действуя по аналогии с предыдущим примером находим

y`<sub>x</sub> = y`_t/x`_t = , t(0,/2) ◄

1) 2) 3) 4)

5) 6) 7) 8)

9) 10) 11) 12)

13) 14) 15) 16)

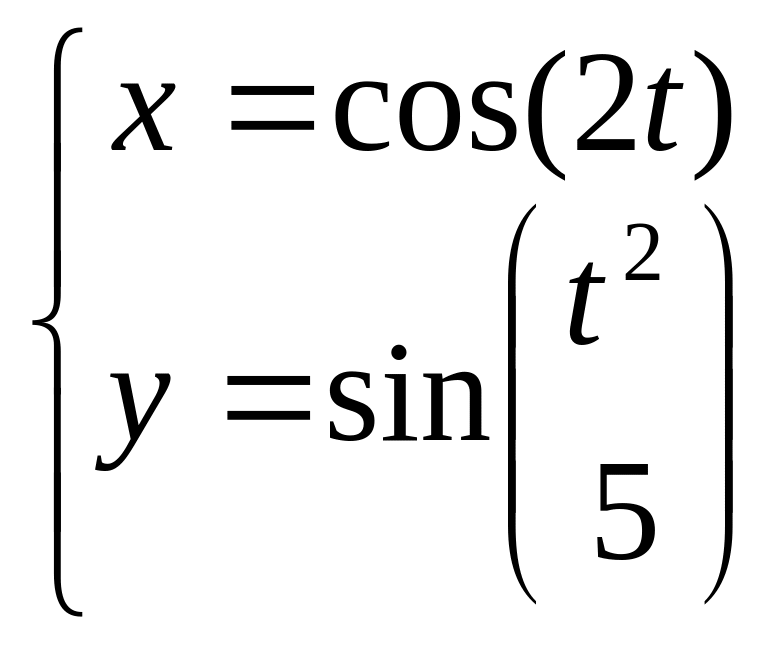
17) 18) 19) 20)

21) 22) 23) 24)

25) 26) 27) 28)

29) 30)