5. Определение синуса и косинуса; тангенса и котангенса на единичной окружности.
Определение. Рассмотрим окружность единичного радиуса с центром в начале координат. Пусть точка на окружности, начав движение в точке М0 (1, 0), прошла по окружности дугу величиной х радиан, или же соответствующий этой точке луч, отрезок, вектор) повернулся на угол х радиан. Пусть Мх – положение точки на окружности в конце движения. Эта точка полностью описывается ее координатами, поэтому для них вводят специальные обозначения.
Ординату точки Мх (или проекцию точки на ось ординат) называют синусом числа х, а абсциссу (или проекцию на ось абсцисс)– косинусом числа х.
Элемент математической культуры как компетенция
ЭМК
Работа с определением
Основная цель работы с определением – выделить существенные признаки определяемого понятия.
Задание
Ответьте на вопрос: «Какие условия надо раскрыть, определяя синус (косинус)?» (выделенные условия последовательно отразите на рисунке).
Задание
Найдите значения синуса и косинуса для углов 0; 2; ; /2; 3/2. и результаты отразите в таблице
Значения синуса и косинуса в характерных точках окружности
Число функция |
0 |
2 |
|
/2 |
3/2 |
Синус |
|
|
|
|
|
Косинус |
|
|
|
|
|
Организация записей как компетенция
Систематизируйте информацию в виде таблицы. Заголовок таблицы должен отражать название системы, название 1-ой строки и 1-го столбца – ее основные характеристики.
Определение. Тангенсом числа х называется отношение синуса данного числа к его косинусу. Котангенсом числа х называется отношение косинуса данного числа к его синусу.
;
.
6. Определение синуса и косинуса; тангенса и котангенса в прямоугольном треугольнике.
Р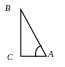
ассмотрим
тригонометрические функции в прямоугольном
треугольнике.
Синусом острого угла прямоугольного
треугольника называют отношение
противолежащего катета к гипотенузе:
sinA =
Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе: cos A =
Задание
Найдите значения синуса и косинуса для углов /6; /4; /3 и результаты отразите в таблице
(
прием
Шаталова с демонстрацией прямоугольного
треугольника с помощью рук).
______________________________________________________________
_______ __________ |
/6 |
/4 |
/3 |
Синус |
|
|
|
Косинус |
|
|
|
Проверка организации записей как компетенции
Дайте название таблице и ее основных характеристик
Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему: tg A = .
Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему: ctg A = .
II Основные тригонометрические тождества (группы тождеств, способы доказательства).