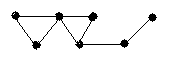
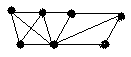
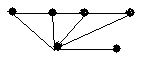
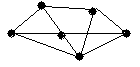
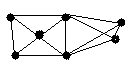
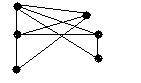
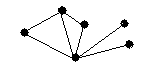
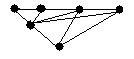
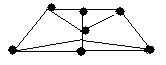
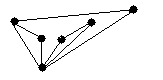
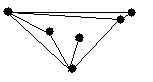
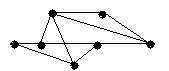
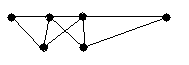
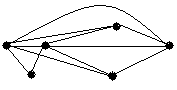
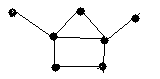
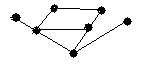
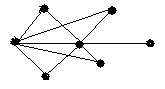
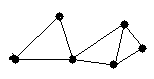
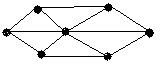
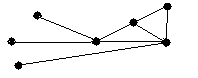
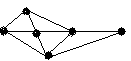
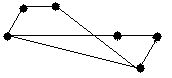
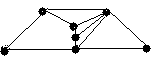
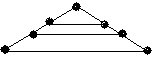
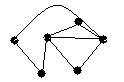
4.3 Варіанти індивідуальних завдань до лабораторної роботи 4

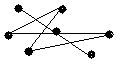
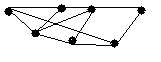
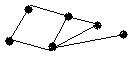
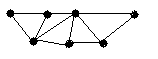
Визначте хроматичні числа для наведених графів відповідно до вашого завдання.

№	граф	№	граф	№	граф
1		11		21
2		12		22
3		13		23
4		14		24
5		15		25
6		16		26
7		17		27
8		18		28
9		19		29
10		20		30

4.4 Контрольні запитання та завдання

1. Дайте визначення графа.

2. Які відмінності між орієнтованим і неорієнтованим графом?

3. Дайте визначення кратності в теорії графів.

4. Який граф називається псевдографом?

5. У якому виді задається інформація щодо графу?

5 РОЗВ’ЯЗАННЯ ЗАДАЧ З ВИКОРИСТАННЯМ ГРАФІВ ТА ЗНАХОДЖЕННЯ НАЙКОРОТШОГО ШЛЯХУ

5.1 Мета роботи

Одержати практичні навички аналізу графів, використовуючи методи функціонального і логічного програмування.

5.2 Підготовка до роботи

Студент повинен знати основні визначення теорії графів.

Послідовність ребер, що з'єднують дві вершини , , називається ланцюгом. Якщо цей ланцюг організований в орграфі, і дуги мають один і той же напрямок з у , то вони називаються шляхом.

Довжиною шляху називається сума довжин дуг, що входять у цей шлях.

Якщо заданий орграф , у якому дуги позначені числами (числа називають вагою, чи довжиною дуг), то він може подаватися як матриця ваг розмірності , що випливає з виду:

, для ;

= Weight(v_i, v_j), де i<>j, якщо в графі існує дуга (v_i, v_j);

, де i<>j, якщо немає ребра (дуги) (v_i, v_j).

Алгоритм Флойда.

Дано: непорожній зважений граф G=(V, E) з довільною вагою ребер (дуг). Потрібно знайти довжини найкоротших шляхів між всіма парами вершин графу, якщо в графі немає циклів (контурів) негативної сумарної довжини, або знайти наявність таких контурів.

Ініціалізація:

1. Побудуємо матрицю розмірності , елементи якої визначаються за правилом:

;

Weight(v_i, v_j), де i<>j, якщо в графі існує дуга (v_i, v_j);

+Ґ, де i<>j, якщо немає ребра (дуги) (v_i, v_j).

2. m:=0.

Основна частина:

1. Побудуємо матрицю по обчислюючи її елементи в такий спосіб:

, де i<>j; (*).

Якщо для якогось i, то в графі існує цикл (контур) негативної довжини, що проходить через вершину v_i; ВИХІД.

2. m:=m+1; якщо , то повторюємо крок (1), інакше елементи останньої побудованої матриці дорівнюють довжинам найкоротших шляхів між відповідними вершинами;

ВИХІД.

КІНЕЦЬ.

Якщо потрібно знайти самі шляхи, то перед початком роботи алгоритму побудуємо матрицю з початковими значеннями елементів Кожний раз, коли на кроці (1) значення буде зменшуватися, відповідно до (*) (тобто коли ), виконаємо присвоювання := Наприкінці роботи алгоритму матриця буде визначати найкоротший шлях між всіма парами вершин: значення буде дорівнювати номеру передостанньої вершини в шляху між i і j (або якщо шлях не існує).

Примітка: якщо граф – неорієнтований, то всі матриці є симетричними, тому досить обчислювати елементи, що знаходяться тільки вище (або тільки нижче) головної діагоналі.

Реалізація алгоритму Флойда

{int c[p][p];// матриця довжин дуг

int t[p][p];// матриця довжин шляхів

int h[p][p];// матриця шляхів

for(int i=0;i<p;i++)

for(int j=0;j<p;j++)

cin>> c[i][j];

for(int i=0;i<p;i++)

for(int j=0;j<p;j++)

{ t[i][j]=c[i][j];

if(c[i][j]==555) h[i][j]=0; // немає дуги з i у j

else h[i][j]=j;// є дуги з i у j

}

for(int i=0;i<p;i++)

{ for(int j=0;j<p;j++)

for(int k=0;k<p;k++)

if(i!=j&&t[j][i]!=555&& i!=k && t[i][k]!=555 &&

( t[j][k]==555 ||t[j][k]>t[j][i]+t[i][k]))

{h[j][k]=h[j][i];// запам'ятати новий шлях

t[j][k]=t[j][i]+t[i][k];// запам'ятати довжину нового шляху

}

for(int j=0;j<p;j++)

if(t[j][j]<0)break;

}

}

5.3 Варіанти індивідуальних завдань до лабораторної роботи 5

Використовуючи варіанти завдань з лабораторної роботи 4, довільно зав-давши номери вершин і відстані, знайти мінімальний шлях для заданих в інтерактивному режимі крапок початку і кінця шляху.

5.4 Контрольні запитання та завдання

1. Дайте визначення хроматичного числа графа.

2. Скільки кольорів необхідно для розфарбування планарного графа?

3. Які відмінності точного і наближеного алгоритму розфарбовування?

4. Чи завжди алгоритм послідовного розфарбовування будує мінімальне розфарбування?