Основные свойства дисперсии
Дисперсия постоянной величины С равна нулю:
Если все значения признака уменьшить или увеличить на некоторую величину (А), то дисперсия не изменится. То дисперсия увеличится или уменьшится в с2 раз.
Правила сложения дисперсии
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
-
общая дисперсия;
-
средняя из внутригрупповых дисперсий;
-
межгрупповая дисперсия.
Общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию.
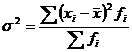
Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней:
где 
-
среднее значение результативного
признака по i-ой группе;
-
общая средняя по совокупности в целом;
-
объем (численность) i-ой группы.
Если факторный признак, по которому производится группировка, не оказывает никакого влияния на результативный признак, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая средняя будет равна нулю.
Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и независящую от признака фактора, положенного в основание группировки.
Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:
где 
-
дисперсия результативного признака в
i-ой группе;
- объем (численность) i-ой группы;
Эмпирический коэффициент детерминации представляет собой долю межгрупповой дисперсии в общей дисперсии.
Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:
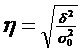
Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.