
Лектор : Мелкумов Ян Сергеевич
Лекция
04.10.12г.
Наиболее часто используемые величины
Средние величины необходимы для качественной однородной величины.
Вычисленные ,для однородной групп величины, называются групповыми средними величинами.
А средние из средних называются общими средними.
Степенные средние и структурные средние
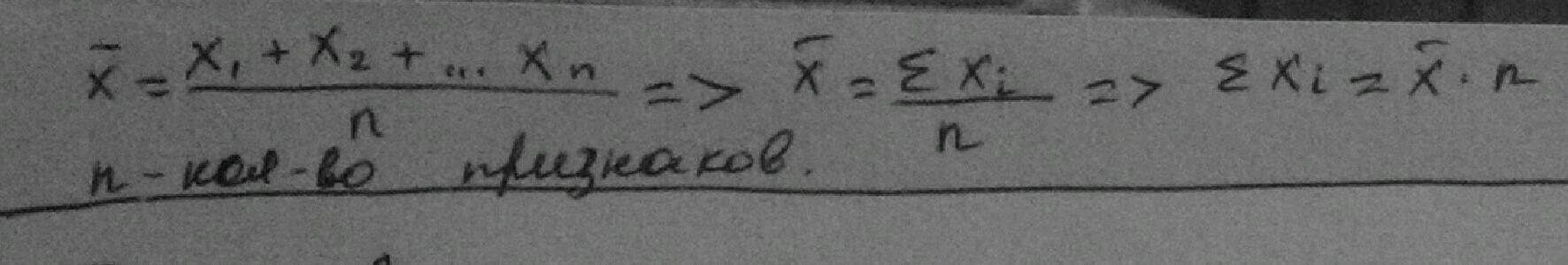
Средняя арифметическая взвешенная
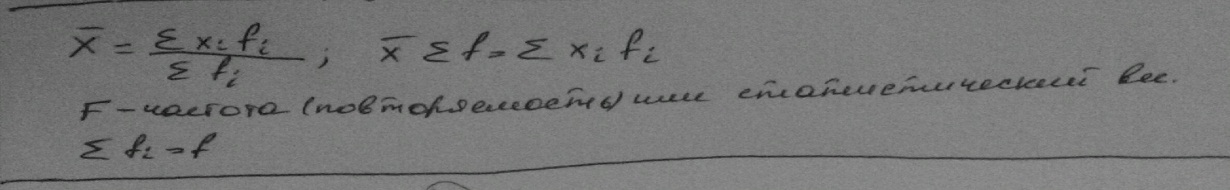
В качестве весов могут использоваться и относительные величины

Например :
По приведенным данным
М з.п руб. |
Число рабочих Fi |
Частость омега(w) |
24,5 |
2 |
2/24=0.0833 |
24,9 |
8 |
8/24=0.3333 |
25,0 |
10 |
10/24=0.4167 |
25,4 |
4 |
4/24=0.1664 |
|
Σfi=24 |
|
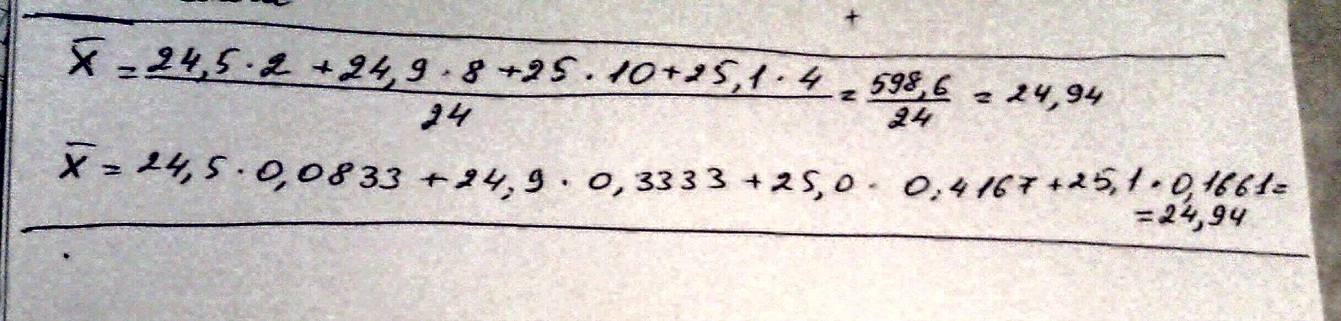
Стаж работы лет хi |
Число рабочихfi |
X =xH+xB/2 |
До 6 |
15 |
- |
6-10 |
25 |
6+10/2=8 |
Свыше 10-…. |
10 |
10+14/2=12 |
Итого |
50 |
|
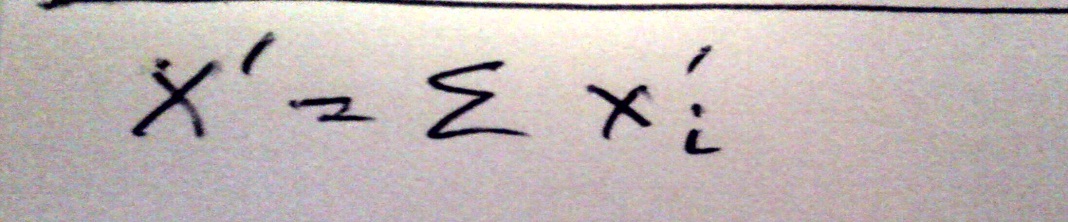
В группах с открытыми интервалами, т.е где отсутствует нижнее или верхнее значения признака хмах-хмин принимается к шагу интервалов последующих или предыдущие группы.
Среднее взвешенное получается и в том случае, если исчисляется средняя величина из групповых средних.
Например:
По 2-м цехам предприятия имеются данные о средней месячнойз.п и численности работников .Определить среднюю з.п по предприятию.
№ Цена |
|
Число рабочих |
Ср. зп. В руб.
|
1 |
|
110 |
1677500 |
2 |
|
90 |
1383300 |
Итого |
|
200 |
3060800 |
Ср.зп х числ.=год зп.
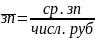
= =
=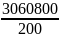 =15304руб.
=15304руб.
Свойствасредней арифметической:
Сумма отклонений индивидуальных значения признака от средней =0
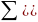 )=0
)=0
)f=0
Нулевое свойство.
Сумма квадратов отклонения индивидуальных значений признаков от средней есть величина минимальная.
)2f=min
3. Если к каждой в варианте прибавить или отнять постоянное число (а),то среднее изменится на это число .
4. если значение признака каждой совокупности разделить или умножить на постоянное число (а),то среднее уменьшится или увеличится в (а) раз.
5. если все частоты веса разделить или умножить на одно и тоже число то среднее не изменится.
Имеются данные об индивидуальных затратах времени 3-мя рабочими на изготовление одной детали .Необходимо рассчитать общую среднюю затрату времени на изготовление этой детали .
-
Номер рабочего
Ср затрата времени на 1 дет в час
Общие затраты вр
Кол-во изгот. дет.
1
0.1
2
0.2
3
0.25
X=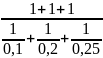 =
=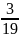 =0,16ч.
=0,16ч.
Полученный результат является средней гармонической не взвешенной.
=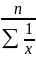
Где n – число случаев
Х-значение признаков
Средняя гармоническая взвешенной рассчитывается как средняя из средних
=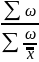
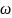 =
*f
=
*f
Например:
По приведенным данным о средней з.п рабочих в 2-х цехах. Рассчитать общую среднюю заработную плату по предприятию.
-
№цеха
Ср. з.п .в руб.хср.
Под з.п
1
15250
1.189500
2
15370
1.380300
Итого
2.572800
=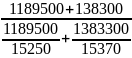 =
=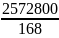 =15314,29руб.
=15314,29руб.
Средняя квадратическая
=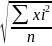 ;
;
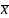 =
=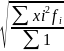
Средняя геометрическая, применяется только при расчетах средних коэффициентов роста или снижения.
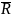 =
=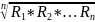
n-число сомножителей под корнем.
=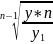
n- число уровня ряда -1,получим число роста.
Например:
В течение рабочей недели (5) банк выдал ряд кредитов. Определить средний недельный темп роста выданных кредитов.
Дни недели |
Сумма выданных кредитов .в 1000р. |
Коэффициент роста или снижения |
Пн |
5858.0 |
- |
Втр |
5970 |
R1
=
|
Ср |
6010 |
R2
=
|
чтв |
6100 |
R3
=
|
пт |
6150 |
R4
=
|
= =1,0122(101,22%)
=1,0122(101,22%)
Является частным случаем.
= ;
;
Средняя не взвешенная степенная
=
m-показатель степени определяющий вид ф.
x-варианты
f-веса при m=1 ,вычисляется формула арифметическая
при m-1-ср. гармоническая
m=0-ср. геометрическая
m=2-ср. квадратическая
Средние обладают св-ом можератности(св-ом не равности ),чем больше степень ,тем больше средняя.
Структурные средние (описательные)к ним относятся мода и медиана.
Мода – это наиболее часто встречающиеся значения признака в изучаемой совокупности.
Например:
Имеются данные, расположенные в порядке возрастания , о средней заработной плате рабочей бригады.
16.120,16120,16.120,16.140,16185,16215,16250.
Мода =16120 –часто встречается.
Медианой, называется значение признака находящееся в центре ранжиренного ряда и делящего этот ряд на две равные части по численности входящих в него единиц совокупности. Для определения места медианы в ранжиреванном ряду, вычисляется ее номер по формуле:
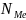 =
=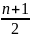 =
=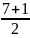 =4
=4
Рассчитанная для данного ряда средняя равняется 16164,29, следовательно 4/7=0.57
Имеют з.п ниже средней.
При четном числе членов ряда также первоначально определяется номер медианы, а затем медиана будет равняться 16120+16140/2=16130
Расчет медианы в ряду распределения
Например:
Имеются данные о распределении группы студентов по росту .Определить среднюю моду и медиану.
Рост студентов в см. х |
Числстуд |
Произведение хifi |
Накопленные частотыs- послед просуммчастоты |
160 |
2 |
320 |
|
162 |
3 |
486 |
|
170 |
8 |
1360 |
13 |
190 |
6 |
1080 |
19 |
|
2 |
380 |
21 |
итог |
21 |
3626 |
|
=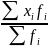 =
= =172,67
см
=172,67
см
M0 =170 см
Для нахождения медианы рассчитываем номер медианы.
NMe
=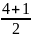 =
=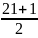 =11
=11
По номеру медианы и накопленным частотам находим медианное значение роста.
М=170см
Расчет модули медианы в интервальном ряду распределения
Нахождение моды и медианы в контрольных по статистике происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. В интервальном вариационном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле:
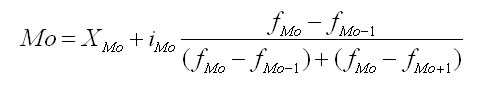
где ХМо — нижняя граница модального интервала; imo — модальный интервал; fм0, fм0-1,, fм0+1 - частоты в модальном, предыдущем и следующем за модальным интервалах. Модальный интервал определяется по наибольшей частоте. Мода широко используется в статистической практике при анализе покупательного спроса, регистрации цен и т. д.
В рядах с не равными интервалами
M0
=
x0+i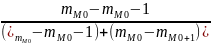
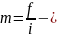 абсолютная
плоскость распределения.
абсолютная
плоскость распределения.
 -
относительная плоскость распределения.
-
относительная плоскость распределения.
𝟂-частость
i-плоскость интервалов
mM0 – следующая за модальным
Медиана в интервальном ряду
Me=x0
+i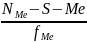
x0 -нижняя граница медианного интервала
i-шаг интервала
-номер медианы
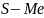 -
накопленные частоты предшествующие
медианному интервалу
-
накопленные частоты предшествующие
медианному интервалу
 -
частота медианного интервала
-
частота медианного интервала

 .в
Руб.
.в
Руб.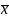 *f
*f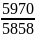 =1,019
=1,019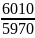 =1,0067
=1,0067 =1,0150
=1,0150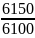 =1,008
=1,008