4.6. The normal distribution approximation to the binomial

distribution

Whenever the number of trials in a binomial experiment is small it is easy to find probabilities of the various values of x, the number of successes, by using formula

As the number of trials increases, however, the effort involved in answering questions about probabilities associated with the experiment quickly becomes laborious.

For instance, suppose that we want to know the probability that in fifteen tosses of a fair coin we toss at least nine heads. You will undoubtedly agree that n =15 is not a large number of trials. However, in order to find we say

P (x=9 or 10 or 11 or 12 or 13 or 14 or 15) =

So we have seven probabilities to compute, after which we must perform the addition. This is not practically difficult, but it takes a fair amount of time.

To find only one of these probabilities, for example, we have

;

.

Therefore

.

Thus, you see that if we were to calculate other six such probabilities we would expend a considerable amount of time and energy.

In such cases, the normal distribution can be used to approximate the binomial probability. Note that, for a binomial problem, the exact probability is obtained by using the binomial formula. If we apply the normal distribution to solve a binomial problem, the probability that we obtain is an approximation to the exact probability.

Example:

According to an estimate, 50% of the people have at least one credit card. If a random sample of 30 persons is taken, what is the probability 19 of them will have at least one credit card?

Solution:

Let n be the total number of persons in the sample, x be the number of persons in the sample who have at least one credit card, and p be the probability that a person has at least one credit card. Then, this is a binomial problem with

n =30; p =0.50; ;

x =19; and .

Using the binomial formula, the exact probability that 19 persons in a sample of 30 have at least one credit card is

Now let us solve this problem using the normal distribution as an approximation to the binomial distribution. For this example,

and

.

Using the normal distribution as an approximation to the binomial involves the following steps:

Step1:

Compute and for the binomial distribution.

To use the normal distribution, we need to know the mean and standard deviation of the distribution. Hence, the first step in using the normal approximation to the binomial distribution is to compute the mean and standard deviation of the binomial distribution. As we know the mean and standard deviation of the binomial distribution are given by

and .

Using these formulas, we obtain

;

.

Step2:

Convert the discrete random variable to a continuous random variable.

The normal distribution applies to a continuous random variable, whereas the binomial distribution applies to a discrete random variable. The second step is to convert the discrete random variable to a continuous random variable by making the correction for continuity.

To make the correction for continuity, we use the interval 18.5 to 19.5 for 19 persons.

Step3:

Compute the required probability using the normal distribution.

The area under the normal curve between x =18.5 and x =19.5 will give us the (approximate) probability that 19 persons possess at least one credit card. We calculate this probability as follows:

For x =18.5; ;

For x =19.5; .

The required probability is given by the area under the standard normal curve between z =1.28 and z =1.64. (Fig 4.21).

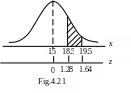
The required probability is

.

Thus, based on the normal approximation, the probability that 19 persons in a sample of 30 will possess at least one credit card is approximately 0.0498. Earlier, using the binomial formula, we obtained the exact probability 0.0509. The error due to using the normal approximation is

. Thus, the exact probability is underestimated by 0.0011 if the normal approximation is used.

Definition:

Let x be the number of successes from n independent trials, each with probability of success p. Then number of successes, x, is a binomial random variable and if (where ) a good approximation is

(4.1)

or if we can use the continuity correction factor to obtain

(4.2)

where Z is a standard normal random variable.

Example:

Let X have a binomial distribution with p =0.6 and n =150. Approximate the probability that

a) x lies between 82 and 101;

b) x is greater than 97.

Solution:

Since , then we will use approximation without using the continuity correction.

Since , we obtain:

a)

.

b)

.

Example:

A large-scale survey conducted two years ago revealed that 30% of the adult population were regular users of alcoholic beverages. If this is still the current rate, what is the probability that in a random sample of 40 adults the number of users of alcoholic beverages will be

a) less than 15

b) 10 or more?

Solution:

For this example

n =40, p =0.3; q =0.7.

Since we must use continuity correction factor to obtain necessary probabilities.

a) .

The probability that 15 out of 40 adults use alcoholic beverages regularly

is 0.8869.

b)

.

Exercises

1. For a binomial probability distribution, n =80 and p =0.50. Let x be the number of successes in 80 trials.

a) Find the mean and standard deviation of the binomial distribution.

b) Find using the normal approximation.

c) Find using the normal approximation

2. For a binomial probability distribution, n =120 and p =0.6. Let x be the number of successes in 120 trials.

a) Find the mean and standard deviation of the binomial distribution.

b) Find using the normal approximation.

c) Find using the normal approximation

3. Find the following binomial probabilities using the normal approximation

a) n =70; p =0.30;

b) n =200; p =0.70;

c) n =40; p =0.25;

d) n =50; p =0.10;

4. According to the statistics, 19% of cars in the city were at least 12 years old in 2004. Assume that this result holds true for the current population of all cars in the city. Random sample of 500 cars are selected at random. Find the probability that

a) exactly 92 cars are at least 12 years old.

b)100 or more cars are at least 12 years old.

c) 90 to 98 cars are at least 12 years old?

5. According to a survey, 30% of credit card holders pay off their balances in full each month. Assume that this result holds true for the current population of credit card holders.

a) Find the probability that in a random sample of 400 credit card holders, exactly 125 pay off their balances in full each month.

b) Find the probability that in a random sample of 400 credit card holders, at least 110 pay off their balances in full each month.

c) What is the probability that in a random sample of 400 credit card holders, 115 to 130 pay off their balances in full each month?

6. A fast food chain store conducted a taste survey before marketing a new hamburger. The results of the survey showed that 70% of the people who tried this hamburger liked it. Encouraged by this result, the company decided to market the new hamburger. Assume that 70% of all people like this hamburger. On a certain day, 40 customers bought this hamburger.

a) Find the probability that exactly 32 of the 40 customers will like this hamburger.

b) What is the probability that 25 or less of the 40 customers will like this hamburger?

c) What is the probability that 31 to 34 of the 40 customers will like this hamburger?

7. According to a survey, 20.8% of the lawyers and judges are women.

a) Find the probability that in a random sample of 200 lawyers and judges, exactly 35 are women.

b) Find the probability that in a random sample of 200 lawyers and judges, at most 45 are women.

c) What is the probability that in a random sample of 200 lawyers and judges, 43 to 50 are women?

8. Of the customers visiting the stereo section of a large electronic store, only 25% make a purchase. If 45 customers visit the stereo section tomorrow, find the probability that more than 10 will make a purchase.

9. The unemployment rate in a city is 7.9%. A sample of 100 persons is selected from the labor force. Approximate the probability that

a) less than 11 unemployed persons are in the sample

b) more than 9 unemployed persons are in the sample.

c) between 8 and 12 unemployed persons are in the sample.

Answers

1. a) ; ; b) 0.7486; c) 0.2262; 2. a) ; ;

b) 0.3557; c) 0.2485; 3. a) 0.0764; b) 0.6393; c) 0.2912; d) 0.8810;

4. a) 0.0413; b) 0.2843; c) 0.3488; 5. a) 0.0378; b) 0.8621; c) 0.5709;

6. a) 0.0525; b) 0.1949; c) 0.1824; 7. a) 0.0371; b) 0.7224; c) 0.3331;

8. 0.7257; 9. a) 0.9082; b) 0.4129; c) 0.5150.