Chapter 3

Discrete random variables and probability distributions

3.1. Random variables

Suppose that experiment of rolling two fair dice to be carried out.

Let X be the sum of outcomes, then X can only assume the values

2, 3, 4, ……., 12 with the following probabilities:

and so on.

The numerical value of random variable depends on the outcomes of the experiment. In this example, for instance, if it is (3, 2), then X is 5, and if it is (6, 6) then X is 12. In this example X is called a random variable.

Definition:

A random variable is a variable whose value is determined by the outcome of a random experiment.

Notationally, we use capital letters, such as X, to denote the random variable and corresponding lowercase x to denote a possible value.

Set of possible values of a random variable might be finite, infinite and countable, or uncountable.

Definition:

A random variable X is called a discrete random variable if it can take on no more than a countable number of values.

Some examples of discrete random variable:

1. The number of employees working at a company.

2. The number of heads obtained in three tosses of a coin.

3. The number of customers visiting a bank during any given day.

A random variable whose values are not countable is called a continuous random variable.

Definition:

A random variable X is called a continuous if it can take any value in an interval.

Here are some examples of continuous random variables:

1. Prices of houses

2. The amount of oil imported.

3. Time taken by workers to learn a job.

3.2. Probability distributions for Discrete Random

Variables

Let X be a discrete random, and x be one of its possible values. The probability that the random variable X takes the value x is denoted by .

Definition:

The probability distribution function, P(x), of a discrete random variable X indicates that this variable takes the value x, as a function of x. That is

, for all values of x.

Example 1:

In the experiment of tossing a fair coin three times, let X be number of heads obtained. Determine and sketch the probability function of X.

Outcome	Value of X
HHH HHT HTH HTT THH THT TTH TTT	3 2 2 1 2 1 1 0

Solution: Table 3.1

First, X is a variable and the number of heads in three tosses of a coin can have any of the values 0, 1, 2, or 3.

We can make a list of the outcomes and the associated values of X. (Table 3.1).

Note that, for each basic outcome there is only one value of X. However, several basic outcomes may yield the same value. We identify the events

(i.e., the collections of the distinct

values of X). (Table 3.2)

Table 3.2.

Numerical value of X as an event	Composition of the event
[X=0] [X=1] [X=2] [X=3]	{TTT} {HTT, THT, TTH} {HHT, HTH, THH} {HHH}

The model of a fair coin entails that 8 basic outcomes are equally likely, so each is assigned the probability 1/8.

The event [X=0] has a single outcome TTT, so its probability is 1/8. Similarly, the probabilities of [X=1], [X=2], and [X=3] are found to be 3/8, 3/8, and 1/8, respectively. Collecting these results, we obtain the probability distribution of X shown in table 3.3.

Table 3.3. The probability distribution of X, the

number of heads in 3 tosses of a coin.

Value of X	Probability
0 1 2 3	1/8 3/8 3/8 1/8
Total	1

Remark: When summed over all possible values of X, these probabilities must add up to 1.

The graphical representation of the probability of X, the number of heads in three tosses of a coin is shown in Fig. 3.1.

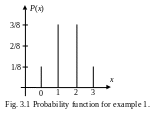
In the development of the probability distribution for a discrete random variable, the following two conditions must always be satisfied:

Properties of probability function of discrete random variables:

Let X be a discrete random variable with probability P(x). Then

1. for any value x.

2. The individual probabilities sum to 1; that is , where the notation indicates summation over all possible values of x.

Another representation of discrete probability distribution is also useful.

Cumulative probability function :

The cumulative probability function, of a random variable X expresses the probability that X does not exceed the value as a function of . That is

,

where the function is evaluated of all values .

Properties of cumulative probability functions for discrete random variables:

Let X be a discrete random variable with cumulative probability function . Then we can show that

1. for every number .

2. If and are two numbers with , then .

Example 2:

In the experiment of rolling a balanced die twice, let X be the minimum of the two numbers obtained. Determine and sketch the probability function and cumulative probability function of X.

Solution:

The possible values of X are 1, 2, 3, 4, 5, and 6, The sample space of this experiment consists of 36 basic outcomes. Hence the probability of any of them is 1/36. In our experiment

P(X=1)=P{(1,1)(1,2)(2,1)(1,3)(3,1)(1,4)(4,1)(1,5)(5,1)(1,6)(6,1)}=11/36

P(X=2)=P{(2,2)(2,3)(3,2)(2,4)(4,2)(2,5)(5,2)(2,6)(6,2)}=9/36

P(X=3)=P{(3,3)(3,4)(4,3)(3,5)(5,3)(3,6)(6,3)}=7/36

P(X=4)=P{(4,4)(4,5)(5,4)(4,6)(6,4)}=5/36

P(X=5) =P {(5, 5) (5, 6) (6, 5)} =3/36

P(X=6) =P {(6, 6)} =1/36

T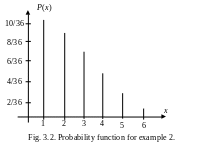 he graphical representation of is shown in Fig.3.2.

Now let us form cumulative probability function.

If is some number less than 1, X can not be less than , so

for all

If is greater than or equal to 1 but strictly less than 2, the only one number less than 2, the only way for X to be less than or equal to is if X=1. Hence

for all

If is greater than or equal to 2 but strictly less than 3, X is less than or equal to the if and only if either X=1 or X =2, so

for .

Continuing in this way we can write cumulative probability function as

The cumulative distribution function of X, , is plotted in Fig. 3.3.

It can be seen that the cumulative probability function increases in steps until the sum is 1.

Example 3:

A consumer agency surveyed all 2500 families living in a small town to collect data on the number of TV sets owned by them. The following table lists the frequency distribution of the data collected by this agency

Number of TV sets owned	0	1	2	3	4
Number of families	120	970	730	410	270

a) Construct a probability distribution table. Draw a graph of the probability distribution.

b) Calculate and draw the cumulative probability function.

c) Find the probabilities: P(X=1), P(X>1), , .

Solution:

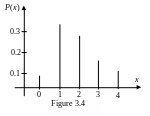
a) In a chapter 2 we learned that the relative frequencies obtained from an experiment or a sample can be used as approximate probabilities. Using the relative frequencies, we can write the probability distribution on the discrete random variable X in the following table.

Number of TV sets owned, x	Probability P(x)
0 1 2 3 4	120/2500=0.048 970/2500=0.388 730/2500=0.292 410/2500=0.164 270/2500=0.108

Figure 3.4 shows the graphical presentation of the probability distribution.

b) Let us form cumulative probability distribution function.

If is less than 0, then

for

If is less than 1, then

for

Continuing in this way, we obtain

This function is plotted in Fig. 3.5.

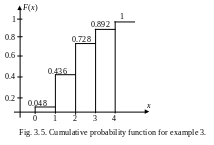
c)

.

Exercises

1. Each of the following tables lists certain values of X and their probabilities. Determine if each of them satisfies the two conditions required for a valid probability distribution.

X	P(x)
0 1 2 3	0.16 0.00 0.43 0.41

a) b) c)

X	P(x)
5 6 7 8	-0.39 0.67 0.31 0.28

X	P(x)
2 3 5	0.22 0.23 0.65

2. For each case, list the values of x and P(x) and examine if the specification represents a probability distribution. If does not, state what properties are violated

a) for

b) for

c) for

d) for

3. The following table gives the probability distribution of a discrete random variable X.

X	0 1 2 3 4 5
P(x)	0.03 0.13 0.22 0.31 0.19 0.12

a) Draw the probability function.

b) Calculate and draw the cumulative probability function.

c) Find ; ; ;

d) Find the probability that x assumes a value less than 3

e) Find the probability that x assumes a value in the interval 2 to 4.

4. Despite all safety measures, accidents do happen at the factory. Let X denote the number of accidents that occur during a month at this factory. The following table lists the probability distribution

of X.

X	0 1 2 3 4
P(x)	0.25 0.30 0.20 0.15 0.10

a) Draw the probability function.

b) Calculate and draw the cumulative probability function.

c) Determine the probability that the number of accidents that will occur during a given month at this company is exactly 4.

d) What is the probability that number of accidents will be at least 2?

e) What is the probability that number of accidents will be less than 3?

f) What is the probability that number of accidents will be

between 2 to 4?

g) Two month are chosen at random. What is the probability that on both

of these months there will be fewer than two accidents?

5. Let X be the number of shopping trips made by family during a month. The following table lists the frequency distribution of X of 1000 families.

X	4 5 6 7 8 9 10
f	70 180 240 210 170 90 40

a) Draw the probability function.

b) Calculate and draw the cumulative probability function.

c) Find the following probabilities ; ; ; .

6. The following table lists the probability distribution of the number of phone calls received per 10-minute period at an office.

Number of phone calls	0 1 2 3 4
Probability	0.12 0.26 0.34 0.18 0.10

Let X denote the number of phone calls received during a certain 10-minute period at this office.

a) Find the probabilities: ; ; ; .

b) Two 10-minute period are chosen at random. What is the probability that at least one of them there will be at least one received call?

7. In successive rolls of a fair die, let X be the number of rolls until the

first 6. Determine the probability function.

8. In a tennis championship, player A competes against player B in consecutive sets and the game continues until one player wins three sets. Assume that, for each set P (A wins) =0.4, P (B wins) =0.6, and the outcomes of different sets are independent. Let X stand for the number of sets played.

a) List the possible values of X and identify the basic outcomes associated with each value.

b) Obtain the probability distribution of X.

Answers

1. a) this is not a valid probability distribution; b) this is not a valid probability distribution; c) this is a valid probability distribution;

2. a) this is a valid probability distribution; b) this is not a valid probability distribution; c) this is a valid probability distribution;

d) this is not a valid probability distribution; 3. c) 0.13; 0.16; 0.62; 0.38; d) 0.38; e) 0.72; 4. c) 0.10; d) 0.45; e) 0.75; f) 0.45; g) 0.3025; 5. c) 0.18; 0.51; 0.70; 0.49; 6. a) 0.26; 0.38; 0.28; 0.78; b) 0.9856;

7. ; 8. b) P (3) =0.2800; P (4) =0.3744;

P (5) =0.3456;