Изменение осадки судна при переходе в воду другой плотности.

При переходе судна в воду иной плотности, которая зависит от солености и температуры, изменяется его осадка. При изменении плотности меняется также сила поддержания . Практически изменение плотности воды не превышает 3 %.

Весовое водоизмещение судна при этом не меняется, и можно записать:

(3.5)

где,

и – исходная плотность и соответствующее объемное водоизмещение;

и – новая плотность и соответствующее объемное водоизмещение.

Из сравнения этих выражений получаем:

(3.6)

Согласно этой формуле получаем:

(3.7)

Так как изменение водоизмещение мало, можно считать судно прямостенным в пределах изменения осадки, т. е. . После подстановки этого выражения в формулу (3.7) получим:

(3.8)

где,

– площадь ватерлинии.

Если учесть, что объемное водоизмещение судна представляет собой , а площадь ватерлинии .

где,

, – коэффициент полноты водоизмещения (общей полноты);

– длина судна между перпендикулярами;

– ширина судна на мидель-шпангоуте;

– осадка судна;

, – коэффициент полноты конструктивной ватерлинии.

Тогда формула (3.8) примет вид:

(3.9)

Очевидно, что при переходе судна в воду с большей плотностью, например, из пресной воды в соленую, оно будет всплывать, и наоборот.

Формулу для изменения осадки при переходе из морской воды в пресную можно представить в другом виде, если использовать выражение (3.3) при подстановке в формулу (3.8) получим:

(3.10)

Принимая и выражая изменение осадки в сантиметрах, получим:

, (3.11)

где,

– число тонн на 1 см осадки, определяется по грузовой шкале.

Практическое занятие № 4

Тема: Условие остойчивости судна. Метацентрические формулы остойчивости. Расчет метацентрических высот по заданному грузовому плану.

Условие остойчивости судна.

Остойчивостью называется способность судна сопротивляться воздействию внешнего кренящего момента и возвращаться в исходное положение равновесия после прекращения действия момента, вызвавшего наклонение под действием восстанавливающего момента .

Понятие остойчивости связывается с действием на судно только моментов (пар сил) и, следовательно, равнообъемными наклонениями – наклонениями, при которых не меняется объем подводной части судна, а только его форма.

Если кренящий момент, приложенный к судну, возрастает постепенно и не вызывает угловых ускорений, а следовательно сил инерции, то при рассмотрении равновесия судна можно пользоваться условиями статического равновесия. Остойчивость при таких наклонениях называется статической.

Остойчивость судна при мгновенно приложенном кренящем моменте называется динамической.

В зависимости от того, какие наклонения рассматриваются, различают поперечную и продольную остойчивость.

В зависимости от величины угла крена поперечную остойчивость разделяют на остойчивость при малых углах наклонения ( ) или начальную остойчивость, и остойчивость на больших углах крена.

При наклонении судна изменяется положение центра подводного объема судна (центра величины наклоненного судна), следовательно, равнодействующая сил поддержания будет приложена в точке . Для оценки остойчивости судна введено понятие метацентрической высоты , которая представляет возвышение метацентра (точка « ») над центром тяжести (точка « ») и может быть положительным или отрицательным. Если равнодействующие сил тяжести и поддержания образуют момент стремящийся увеличить угол крена судна – то судно не остойчиво , (рис.4.1).

Если возникает момент , стремящийся вернуть судно в исходное прямое положение, то судно остойчиво , (рис. 4.2).

Момент называется восстанавливающим моментом и равен он произведению одной из сил пары на плечо

(4.1)

где,

– сила тяжести, т;

– весовое водоизмещение, т;

– плотность забортной воды, т/м³;

– объемное водоизмещение, т;

– сила поддержания, т;

– плечо статического угла крена, м.

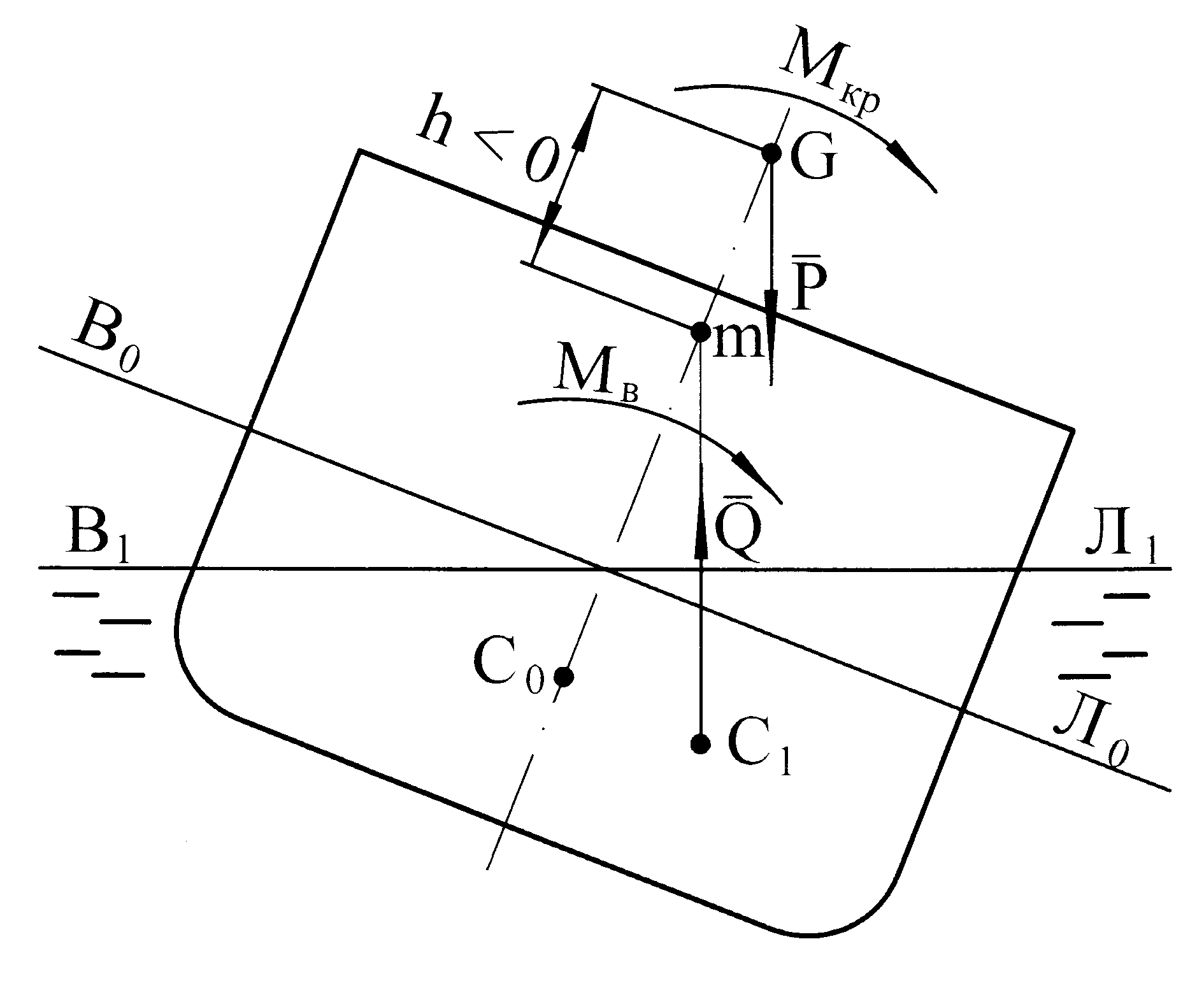
Рисунок 4.1 – Неостойчивое судно.

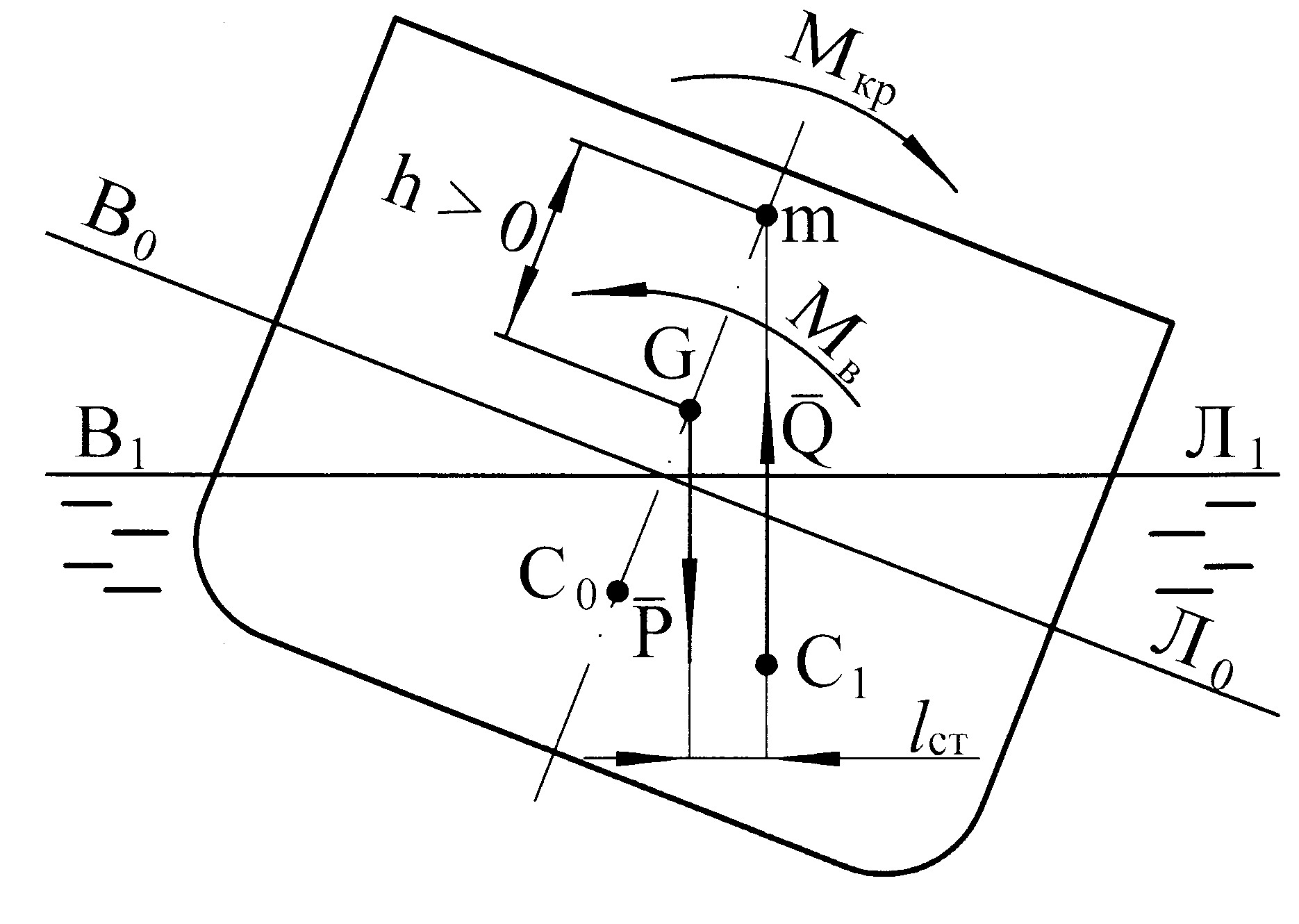
Рисунок 4.2 – Остойчивое судно.

Метацентрические формулы остойчивости.

Для оценки остойчивости судна при наклонениях в поперечном или продольном направлении, достаточно определить его поперечную и продольную метацентрические высоты.

Поперечная и продольная метацентрическая высота зависит от формы корпуса судна, соотношения его главных размерений, состояния нагрузки, наличия жидких и перемещающихся грузов, расположения центра величины (ЦВ) и центра тяжести (ЦТ), а также метацентров и (рис. 4.3 и рис. 4.4).

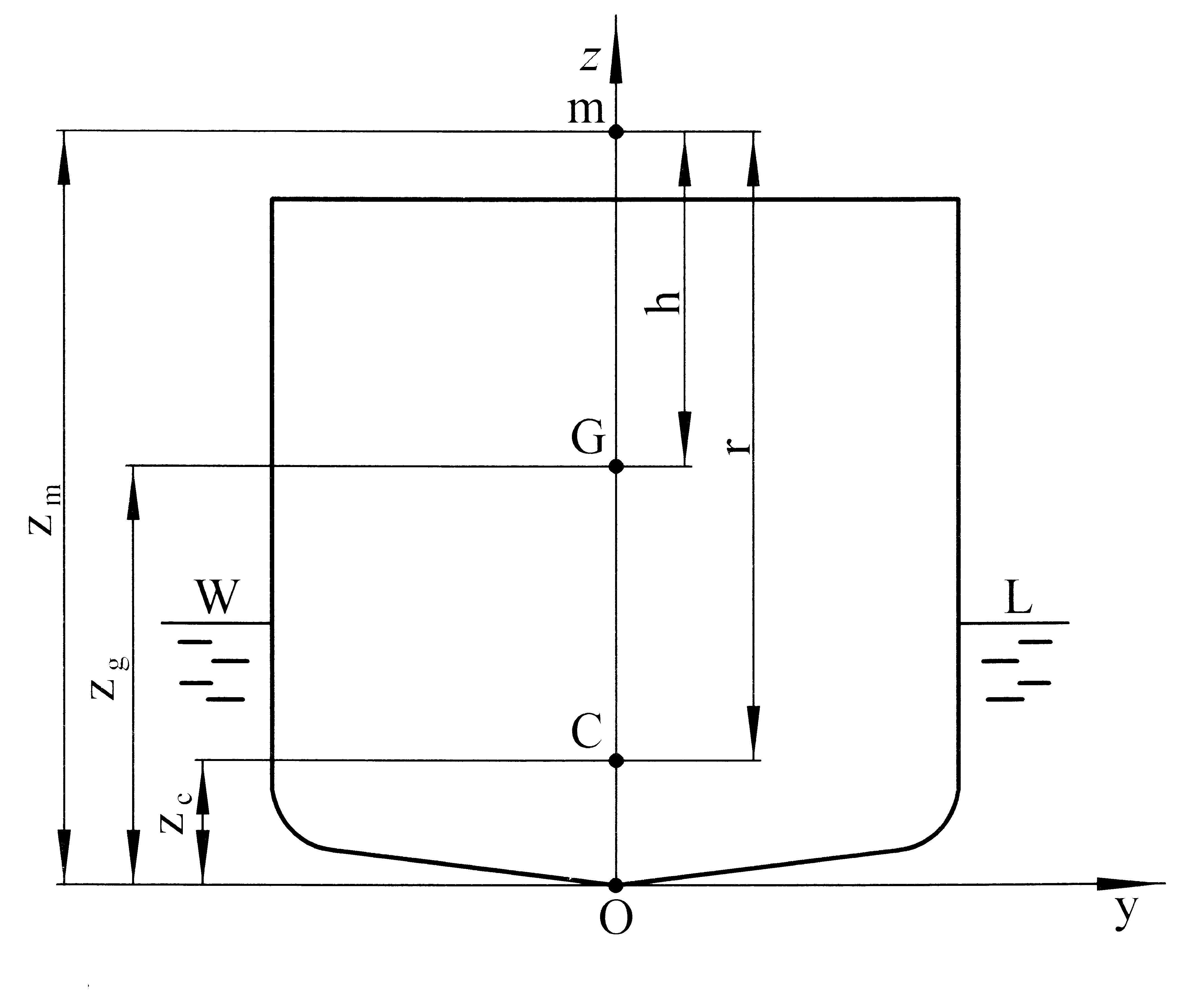
Рисунок 4.3 – Расчет поперечной метацентрической высоты.

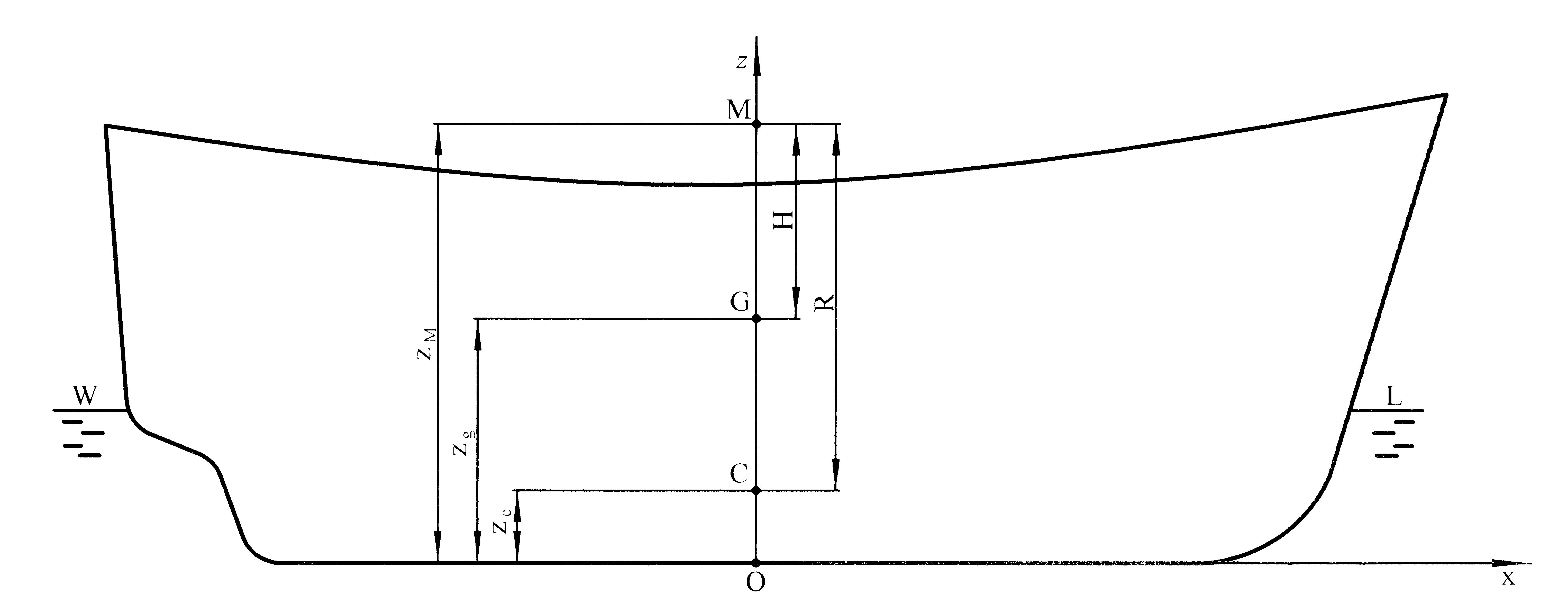
Рисунок 4.4 – Расчет продольной метацентрической высоты.

Поперечную и продольную метацентрическую высоту можно определить по следующим формулам:

(4.2)

(4.3)

где,

– аппликата поперечного и продольного метацентра, определяются по кривым элементам теоретического чертежа или гидростатической таблице, для данной осадки ;

– аппликата центра тяжести судна, вычисляется при составлении грузового плана, для данной осадки ;

– аппликата центра величины судна, определяется по кривым элементам теоретического чертежа или гидростатической таблице, для данной осадки ;

– поперечный и продольный метацентрические радиусы, определяются по кривым элементам теоретического чертежа или гидростатической таблице, для данной осадки .