Глава 3. Линейные пространства
3.18. Векторное произведение векторов
Определение
3.18.1. Векторным
произведением вектора
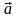 на
вектор
на
вектор
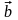 называется вектор
называется вектор
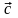 ,
обозначаемый символом
=
,
обозначаемый символом
=
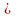 и определяемый следующим образом:
и определяемый следующим образом:
1) модуль
вектора
равен произведению модулей векторов
и
на синус угла между этими векторами
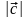 =
=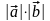 sin,
где
sin,
где
 .
.
2) вектор перпендикулярен каждому из векторов и ;
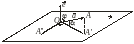
3) вектор направлен так, что упорядоченная тройка векторов , , является правой (рис. 3.18.1).
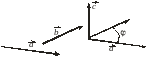
Рис.3.18.1
Ясно, что если хотя бы один из векторов и нулевой, то их векторное произведение есть нулевой вектор.
Наряду с введенным обозначением будем использовать, когда это удобно, и другую форму записи векторного произведения [ , ].
Лемма
3.18.1.
Векторное
произведение двух неколлинеарных
векторов
и
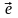 ,
причем
— произвольный вектор, а
— единичный вектор, равно вектору
,
причем
— произвольный вектор, а
— единичный вектор, равно вектору
 ,
построенному следующим образом:
,
построенному следующим образом:
1) векторы и приведены к общему началу О;
2) вектор
 получен
в результате проектирования вектора
получен
в результате проектирования вектора
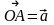 на плоскость ,
перпендикулярную к вектору
и проходящую через О;
на плоскость ,
перпендикулярную к вектору
и проходящую через О;
3) вектор построен с помощью поворота вектора в плоскости на угол, равный 90, так чтобы упорядоченная тройка , , была правой.
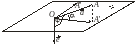
Доказательство. Пусть — угол между векторами и , — угол между вектором и его проекцией . Нетрудно видеть, что вектор лежит в той же плоскости, что и векторы и (рис. 3.18.2, 3.18.3). Поэтому векторы и перпендикулярны плоскости, определяемой векторами , , и, следовательно, они коллинеарны. Кроме того,
Рис. 3.18.2 |
Рис. 3.18.3 |
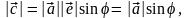
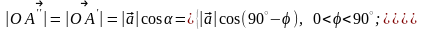
поэтому
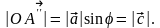 По построению тройка векторов
,
,
— правая. В силу того, что 0 < < 90,
тройка векторов
,
,
также будет правой. Однако, по определению
векторного произведения тройка
,
,
является правой, поэтому
По построению тройка векторов
,
,
— правая. В силу того, что 0 < < 90,
тройка векторов
,
,
также будет правой. Однако, по определению
векторного произведения тройка
,
,
является правой, поэтому
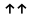 ,
отсюда
=
,
отсюда
=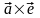 .
.
Теорема 3.18.1.
Необходимым
и достаточным условием коллинеарности
двух ненулевых векторов
и
является равенство
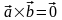 .
.
Доказательство.
Необходимость.
Пусть
и
коллинеарны. Тогда угол
между ними равен 0, если они сонаправлены
и равен 180,
если они противоположно направлены, но
в любом случае
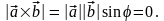
Достаточность.
Пусть
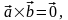 следовательно,
следовательно,
|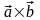 | = 0
| = 0
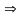
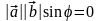 sin = 0
= k,
k Z
sin = 0
= k,
k Z
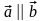 .
.
Теорема
3.18.2 (свойства векторного произведения).
Для
любых трех векторов
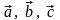 и произвольного числа
справедливы соотношения:
и произвольного числа
справедливы соотношения:
1.  (антикоммутативность);
(антикоммутативность);
2. 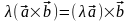 (ассоциативность
относительно числового
множителя);
(ассоциативность
относительно числового
множителя);
3. ( + ) = + (дистрибутивность относительно суммы векторов);
4.
=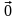 (для любого
вектора
).
(для любого
вектора
).
Доказательство.
Свойство 1. Будем
считать, что векторы
и
неколлинеарные, иначе свойство 1
очевидно. Пусть векторы
=
и
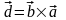 ,
а
— угол между
и
.
Ясно, что
,
а
— угол между
и
.
Ясно, что
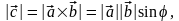
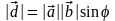
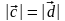 .
.
Понятно,
что векторы
и
 коллинеарные, так как они перпендикулярны
плоскости, в которой лежат векторы
и
.
Согласно определению векторного
произведения, упорядоченные тройки
векторов
,
,
и
,
,
являются правыми, а это влечет
противоположную направленность векторов
и
(рис. 3.18.4). Следовательно, векторы
и
— противоположные, т. е.
.
коллинеарные, так как они перпендикулярны
плоскости, в которой лежат векторы
и
.
Согласно определению векторного
произведения, упорядоченные тройки
векторов
,
,
и
,
,
являются правыми, а это влечет
противоположную направленность векторов
и
(рис. 3.18.4). Следовательно, векторы
и
— противоположные, т. е.
.
С

Рис. 3.18.4
войство 2. Будем считать, что векторы и неколлинеарные, 0. Пусть
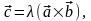
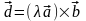 ,
,
,
,
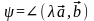 .
Ясно (рис.3.18.5, 3.18.6), что
.
Ясно (рис.3.18.5, 3.18.6), что
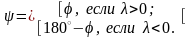
Векторы и коллинеарны, так как они перпендикулярны плоскости, определяемой векторами и .
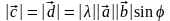 .
.
Если
> 0

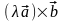
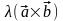 .
.
Если
< 0
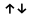 .
.
Таким образом,
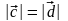 ,
,
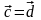 .
.
Рис. 3.18.5
|
Рис. 3.18.6 |
Свойство 3. Будем
считать, что
 ,
,
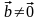 и
и
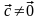 .
Докажем сначала справедливость равенства
.
Докажем сначала справедливость равенства
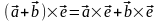 ,
где
— единичный вектор. Будем предполагать,
что векторы
,
,
некомпланарны.
,
где
— единичный вектор. Будем предполагать,
что векторы
,
,
некомпланарны.
Приведем
векторы
,
, к общему началу О.
Спроектируем
векторы
,
к общему началу О.
Спроектируем
векторы
,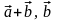 на плоскость ,
перпендикулярную вектору
и проходящую через точку О.
Получаем соответственно векторы
,
на плоскость ,
перпендикулярную вектору
и проходящую через точку О.
Получаем соответственно векторы
, ,
,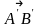 (рис. 3.18.7). Построим векторы
,
(рис. 3.18.7). Построим векторы
,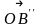 ,
,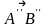 как указано в лемме. По определению
суммы векторов
=
+
.
Но в силу леммы
=
как указано в лемме. По определению
суммы векторов
=
+
.
Но в силу леммы
=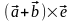 ,
=
,
=
,
=
,
=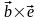 ,
поэтому
=
+
.
,
поэтому
=
+
.
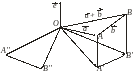
Рис. 3.18.7
Ясно, что если , , компланарны, то доказательство и соответствующий чертеж значительно упрощаются.
Пусть
— орт вектора
,
тогда
 ,
поэтому
,
поэтому
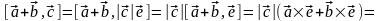
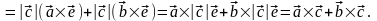
Свойство 4. Справедливость указанного соотношения непосредственно вытекает из определения векторного произведения.
Доказанные свойства позволяют при векторном перемножении векторных многочленов выполнять действия почленно и производить объединение числовых множителей. При этом нужно тщательно следить за порядком векторных множителей.
Теорема 3.18.3.
Векторное
произведение векторов
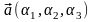 и
и
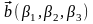 ,
заданных
своими аффинными координатами, вычисляется
по формуле
,
заданных
своими аффинными координатами, вычисляется
по формуле
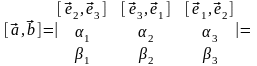
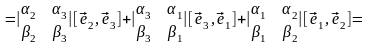
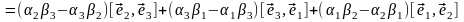 . (3.18.1)
. (3.18.1)
Доказательство.
По определению аффинных координат
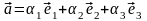 ,
,
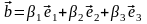 ,
поэтому с учетом свойств векторного
произведения
,
поэтому с учетом свойств векторного
произведения
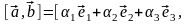
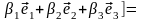
=
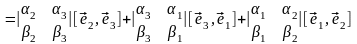 =
=
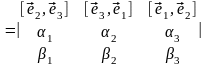 .
.
Следствие 3.18.1.
Векторное
произведение векторов
 и
и
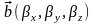 ,
заданных
своими декартовыми прямоугольными
координатами, находится по формуле
,
заданных
своими декартовыми прямоугольными
координатами, находится по формуле
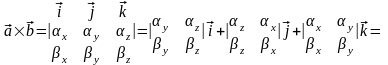
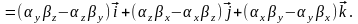 (3.18.2)
(3.18.2)
Доказательство.
Пусть
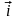 ,
,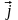 ,
,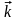 —
ортонормированный базис декартовой
прямоугольной системы координат.
Поскольку
—
ортонормированный базис декартовой
прямоугольной системы координат.
Поскольку
 ,
то в формуле (3.18.1)
,
то в формуле (3.18.1)
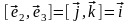 ,
,
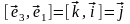 ,
,
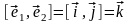 .
С учетом равенств
.
С учетом равенств
 ,
,
 получаем формулу (3.18.2).
получаем формулу (3.18.2).
Теорема 3.18.4. Модуль векторного произведения двух неколлинеарных векторов и равен площади S параллелограмма, построенного на этих векторах, после приведения их к общему началу, т. е.
| | = S. (3.18.3)
Доказательство.
Известно, что площадь параллелограмма
равна произведению длин его смежных
сторон на синус угла между ними
(рис. 3.18.8) SOBDA = 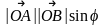 ,
где
— угол между векторами
,
где
— угол между векторами
 и
и
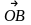 .
Отсюда
.
Отсюда
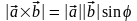 = SOBDA.
= SOBDA.
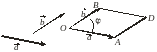
Рис. 3.18.8
Следствие 3.18.2.
Векторное
произведение
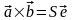 ,
где
— орт векторного произведения
,
S — площадь параллелограмма, построенного
на приведенных к общему началу векторах
и
.
,
где
— орт векторного произведения
,
S — площадь параллелограмма, построенного
на приведенных к общему началу векторах
и
.
Следствие 3.18.3. Площадь параллелограмма, построенного на двух неколлинеарных векторах и , заданных своими прямоугольными декартовыми координатами и приведенных к общему началу, определяется по формуле
S = 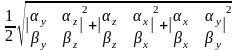 .
.
Указанное равенство вытекает из соотношений (3.18.3), (3.18.2) и формулы для определения модуля вектора.