
- •Введение
- •1. Основные понятия теории вероятностей
- •2. Повторение незавИсИмых опытов
- •3. Случайные величины и их числовые характеристики
- •4. Система двух случайных величин и регрессия
- •Закон распределения двумерной случайной величины
- •5. Основы математической статистики
- •Контрольная работа 4
- •Задача 2.
- •Контрольная работа 5
- •6. Линейное программирование. Основные понятия и экономическая интерпретация
- •6.1. Задача лп
- •6.2. Примеры постановки задач лп
- •6.3. Геометрическая интерпретация задачи лп. Графическое решение
- •6.4. Основные формы задачи лп
- •6.5. Симплексный метод и приведение задачи лп к правильной форме
- •6.6. Признаки оптимальности начального допустимого плана
- •7. Метод искусственного базиса
- •8. Двойственные задачи лп
- •9. Транспортная задача и метод потенциалов
- •Контрольная работа 6
- •Рекомендательный библиографический список
- •Значения в зависимости от числа степеней свободы m и уровня значимости ( – доверительная вероятность)
- •Содержание
6.2. Примеры постановки задач лп
Задача о производстве. Мастерская изготавливает столы и шкафы. В запасе имеется 15 и 10 м3 древесины 1-го и 2-го сорта соответственно, а также ресурсы труда – 200 человеко-ч. Расходы ресурсов на производство одного изделия следующие:
Изделия |
1 сорт |
2 сорт |
Ресурсы труда |
Стол |
0,5 |
0,2 |
10 |
Шкаф |
1,2 |
1 |
15 |
Доход от продажи одного стола равен 100 условных единиц, а от продажи одного шкафа – 150 условных единиц.
Найти план производства, максимизирующий доход.
Поставим задачу
математически. Пусть запланированное
количество столов равно
![]() ,
а шкафов –
,
а шкафов –
![]() ,
т.е. план производства
,
т.е. план производства
![]() .
Тогда ограничения по ресурсам,
соответственно по использованным
для производства древесины 1-го,
2-го сорта и труду, примут вид следующих
неравенств:
.
Тогда ограничения по ресурсам,
соответственно по использованным
для производства древесины 1-го,
2-го сорта и труду, примут вид следующих
неравенств:
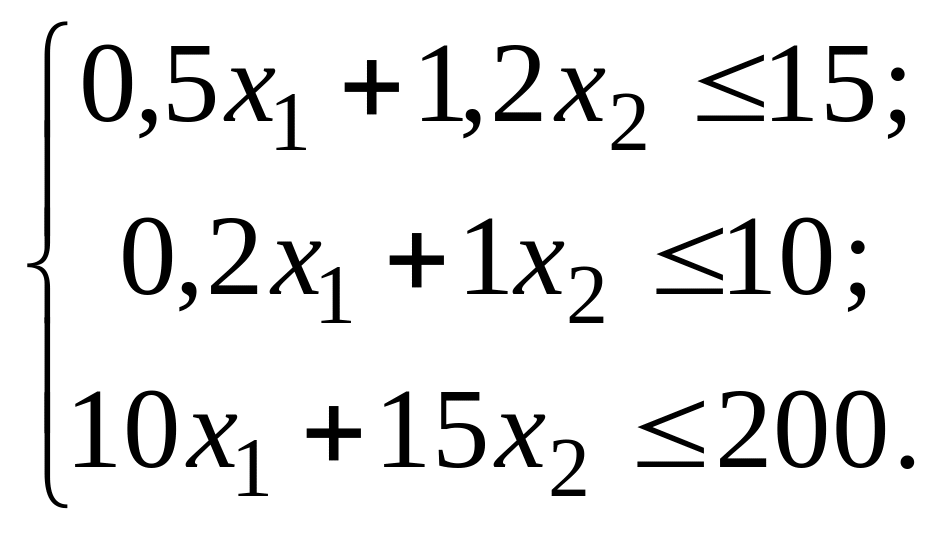
Ясно, что выполняются и смысловые
ограничения
![]() .
.
Доход, т.е. целевая
функция этой задачи, при выполнении
плана
равен
![]() .
Таким образом, математически задача
оптимизации плана производства сводится
к задаче ЛП:
.
Таким образом, математически задача
оптимизации плана производства сводится
к задаче ЛП:
![]()
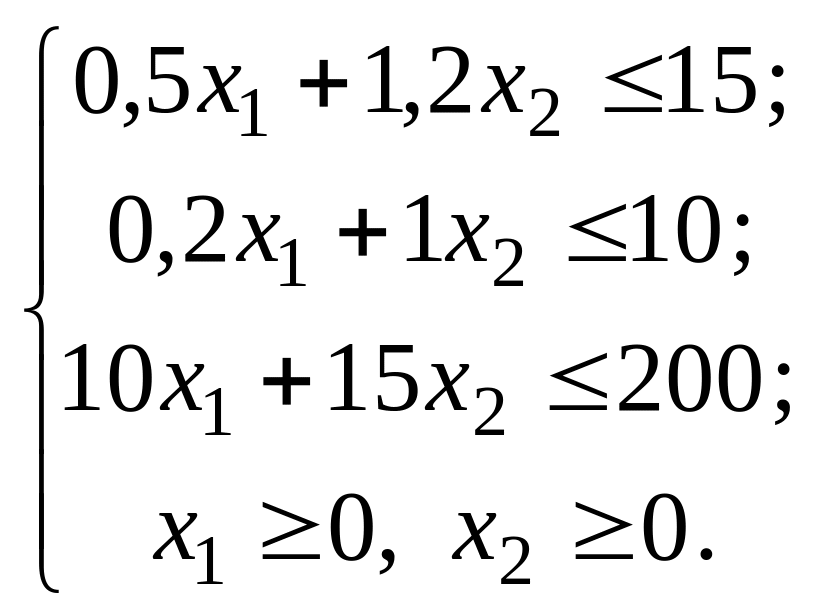
Задача о диете.
Из двух продуктов
и
![]() надо
составить диету, которая удовлетворяет
ежесуточной потребности организма в
белках, жирах, углеводах и требует
наименьших затрат. Распределение белков,
жиров и углеводов по продуктам, потребности
организма и стоимости продуктов
следующие:
надо
составить диету, которая удовлетворяет
ежесуточной потребности организма в
белках, жирах, углеводах и требует
наименьших затрат. Распределение белков,
жиров и углеводов по продуктам, потребности
организма и стоимости продуктов
следующие:
Продукты |
Белки |
Жиры |
Углеводы |
Стоимость 1 кг |
A |
а1 |
а2 |
а3 |
S1 |
B |
b1 |
b2 |
b3 |
S2 |
Потребность |
a |
b |
c |
|
Если
![]() – количество продукта A
и
– количество продукта A
и
![]() – количество продукта B,
т.е. рацион
,
то затраты
– количество продукта B,
т.е. рацион
,
то затраты
![]() ,
а ограничения состоят в покрытии
потребностей соответственно по белкам,
жирам и углеводам:
,
а ограничения состоят в покрытии
потребностей соответственно по белкам,
жирам и углеводам:
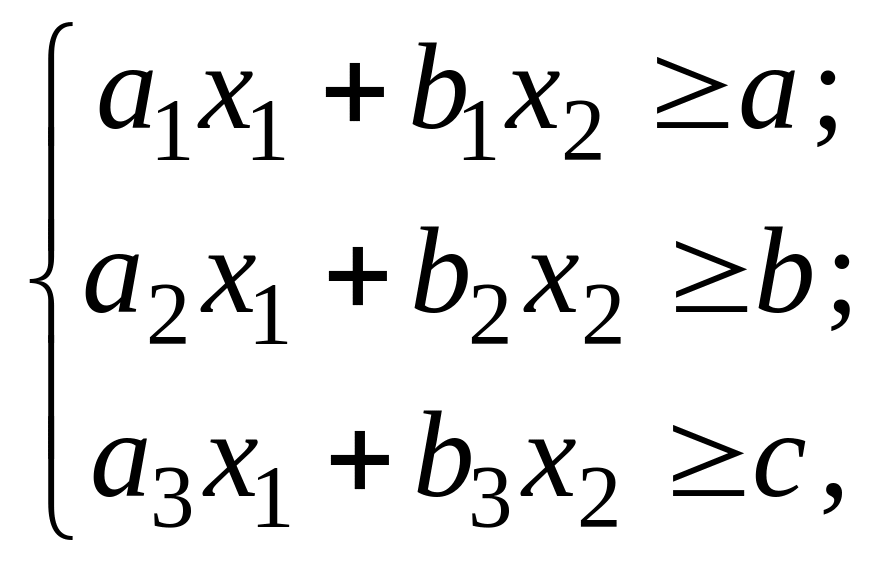
где
![]() .
.
6.3. Геометрическая интерпретация задачи лп. Графическое решение
В многомерном
пространстве
линейное уравнение
![]() или
или
![]() задает гиперплоскость с вектором нормали
задает гиперплоскость с вектором нормали
![]() ,
которая является аналогом плоскости
для
(или прямой для
,
которая является аналогом плоскости
для
(или прямой для
![]() ).
Соответственно, линейное неравенство
).
Соответственно, линейное неравенство
![]() или
или
![]() задает замкнутое полупространство.
Тогда система таких неравенств задает
пересечение соответствующих
полупространств, т.е. геометрически
область ограничений G
для задачи ЛП есть некоторый многомерный
многогранник, называемый симплексом.
Симплекс, как и обычные многогранники,
является выпуклым телом, лежит по одну
сторону от любой своей грани (содержит
весь отрезок, соединяющий любые две
свои точки).
задает замкнутое полупространство.
Тогда система таких неравенств задает
пересечение соответствующих
полупространств, т.е. геометрически
область ограничений G
для задачи ЛП есть некоторый многомерный
многогранник, называемый симплексом.
Симплекс, как и обычные многогранники,
является выпуклым телом, лежит по одну
сторону от любой своей грани (содержит
весь отрезок, соединяющий любые две
свои точки).
Для
целевой функции
![]()
![]() вектор – градиент
grad f =
вектор – градиент
grad f = ![]()
![]() является постоянным вектором. Поэтому
при движении от любой допустимой точки
является постоянным вектором. Поэтому
при движении от любой допустимой точки
![]() (для
(для
![]() Ǿ)
по направлению градиента в области
ограничений (в симплексе) значения
целевой функции увеличиваются до тех
пор, пока не будет достигнута граница
симплекса (грань). Таким образом, в
стандартной форме задачи ЛП оптимальное
решение, если оно есть, достигается на
границе симплекса, а так как к этой форме
можно привести любую задачу ЛП, то это
верно и для любой задачи ЛП.
Ǿ)
по направлению градиента в области
ограничений (в симплексе) значения
целевой функции увеличиваются до тех
пор, пока не будет достигнута граница
симплекса (грань). Таким образом, в
стандартной форме задачи ЛП оптимальное
решение, если оно есть, достигается на
границе симплекса, а так как к этой форме
можно привести любую задачу ЛП, то это
верно и для любой задачи ЛП.
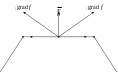
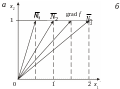
Рис.6. Сравнение градиента и граней симплекса
Если градиент перпендикулярен достигнутой грани, то она является множеством уровня целевой функции, где функция принимает одно и то же значение (постоянна). Поэтому движение дальше в направлении градиента (в сторону увеличения значения целевой функции) по этой грани невозможно (как и по другим граням в силу выпуклости симплекса) (рис.6, б).
Эта грань и будет множеством оптимальных решений (бесконечное множество альтернативных решений).
Если градиент не перпендикулярен грани, то возможно движение по этой грани в направлении градиента, а точнее – в направлении проекции градиента на эту грань (рис.6, б) и, следовательно, увеличение значения целевой функции до перехода на следующую грань, для которой следует повторить эту процедуру. В итоге либо движение по симплексу неограниченно, т.е. неограниченно увеличивается целевая функция и у нее нет наибольшего значения (задача ЛП не имеет решения), либо через несколько шагов попадем на грань, перпендикулярную grad f (множество решений), либо окажемся в вершине, из которой невозможно движение в направлении градиента для увеличения значения целевой функции (вершина A на рис.7). В последнем случае получим единственное решение. Таким образом, оптимальное значение, если оно есть, достигается всегда по крайней мере в одной из вершин симплекса.
Такое геометрическое
(графическое) решение практически
возможно только для случая двух
переменных, т.е. на плоскости
.
Тогда, находясь на стороне многоугольника
(двумерный симплекс), следует определить
направление движения по ней (влево или
вправо). Для этого достаточно определить
расположение градиента относительно
нормали
![]() стороны (см. рис.6, а).
стороны (см. рис.6, а).
Рис.7.
Геометрическое решение задачи ЛП
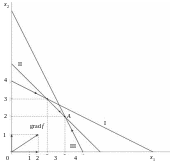
![]() при ограничениях вида
при ограничениях вида
![]()
Решение. Здесь
![]() – уравнение стороны I
– уравнение стороны I
![]()
![]() ;
;
![]() – уравнение стороны II
– уравнение стороны II
![]() ;
;
![]() – уравнение стороны III
– уравнение стороны III
![]() ;
;
![]() ,
grad f =
,
grad f = ![]() .
.
По диаграмме взаимного расположения нормалей и градиента (рис.6, а) и по проекциям градиента на оси координат (рис.7) определим направления движения по границам области ограничений и оптимальное решение, т.е. вершину A (рис.7), координаты которой есть пересечение сторон II и III:
![]()
![]()
![]()
![]() .
.
Заметим, что для построения
области ограничений достаточно найти
точки пересечения сторон I
и II, II и III
и точки пересечения осей координат и
границы I (наименьшая
точка пересечения на оси
![]() )
и границы II (наименьшая
точка пересечения на оси
)
и границы II (наименьшая
точка пересечения на оси
![]() ).
).
