7. Метод искусственного базиса

Для того, чтобы получить правильную форму задачи ЛП без предварительного приведения к ней, используется метод искусственного базиса. В канонической задаче ЛП введем в левую часть уравнений системы ограничений по одной неотрицательной (базисной) искусственной переменной с коэффициентом единица так, чтобы матрица ограничений для новой задачи стала правильной. Достаточно для этого ввести столько искусственных переменных в уравнения, чтобы число правильных столбцов (с учетом уже бывших в исходной матрице А) стало равно числу уравнений, т.е. строк матрицы А. для переменных , где – искусственные переменные, составим новую целевую функцию – , где параметр должен выбираться достаточно большим по сравнению со всеми величинами, которые могут получиться при конечном числе шагов при решении задачи ЛП. Таким образом, наряду с исходной f -задачей: , , сформулирована новая -задача: , , .

Новая задача с искусственными переменными имеет правильную матрицу и легко приводится к правильному виду, если исключить базисные переменные из новой целевой функции. Очевидно, если – допустимый план f -задачи, следовательно, – допустимый план для -задачи.

Теорема 3.

1. Если для -задачи оптимальный план , т.е. все искусственные переменные равны нулю, то соответствующий план будет оптимальным для f -задачи.

2. Если в оптимальном плане -задачи есть искусственные переменные, не равные нулю, то ограничения для f -задачи несовместны (исходная задача неразрешима).

Теорема 4. Если целевая функция -задачи неограниченна снизу (теорема 2, п.2), то f -задача неразрешима.

Пример 21. Для канонической задачи

где , , .

Введем искусственные переменные . Ограничения и целевая функция теперь имеют вид

.

Расширенная матрица -задачи

,

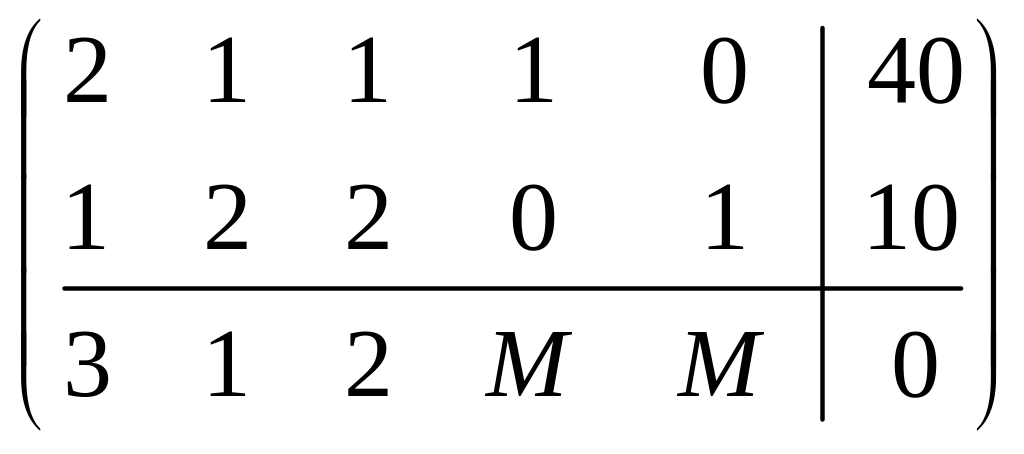
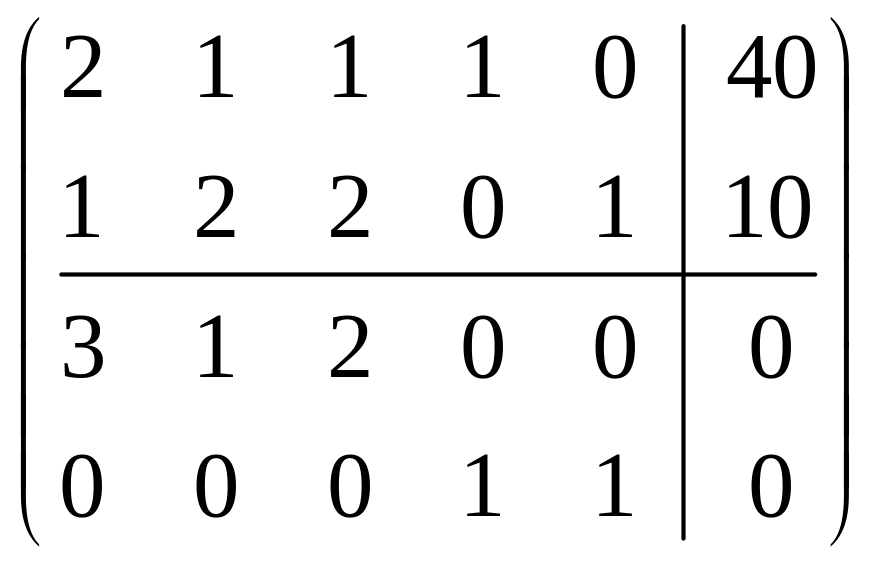где для коэффициентов целевой функции при параметре M введена вторая дополнительная строка. Если в дополнительных строках в каком-то столбце стоят два числа , коэффициент при соответствующей переменной в целевой функции равен . Тогда удобно производить действия с параметром М, вычисляя только коэффициент при этом параметре М, с которым он входит в целевую функцию -задачи.

Эта задача становится правильной, если исключить базисные (искусственные) переменные и из целевой функции:

.

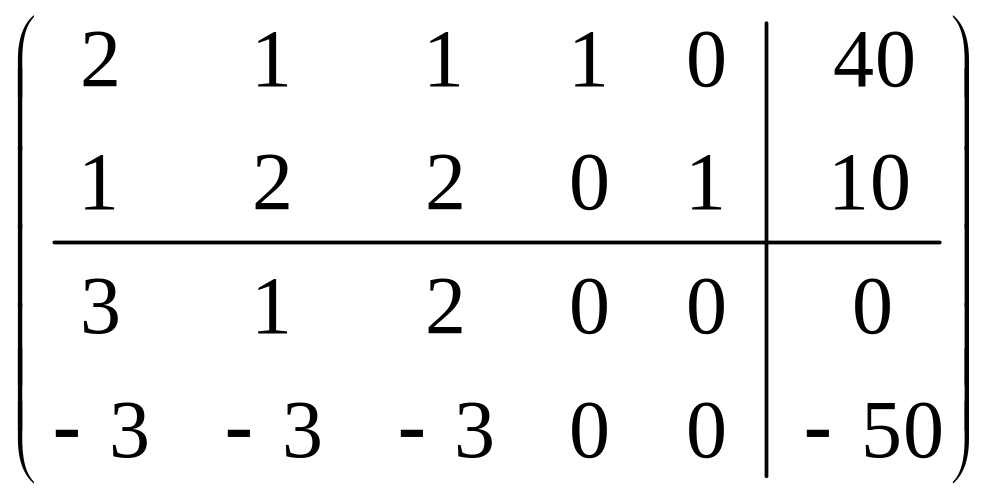Так как большое , то коэффициенты при свободных переменных , , и оптимальности нет. Выбирая самый маленький коэффициент , для достижения оптимальности проводим симплексные преобразования:

.

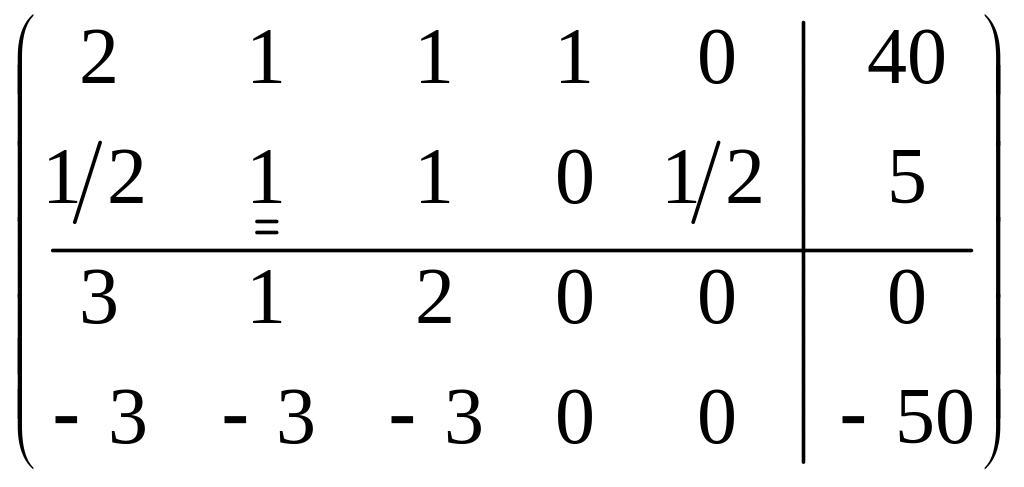
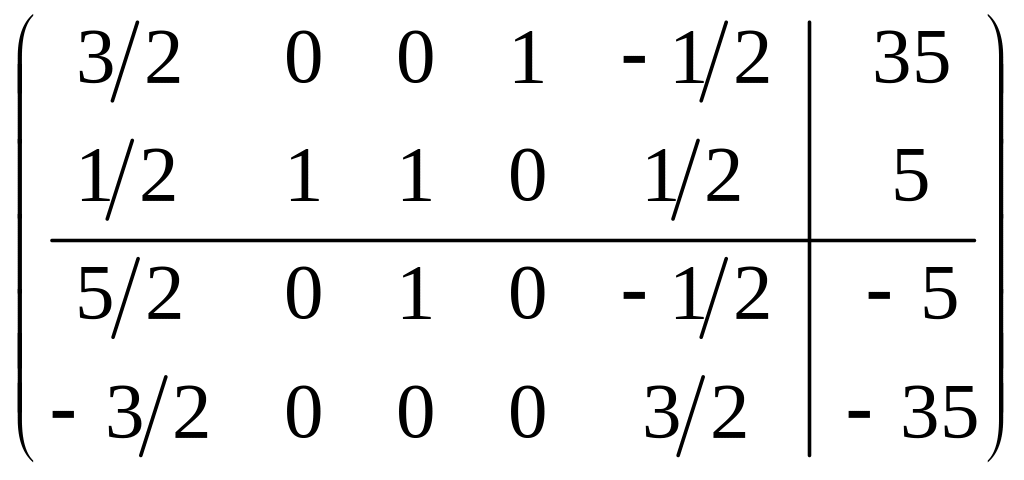
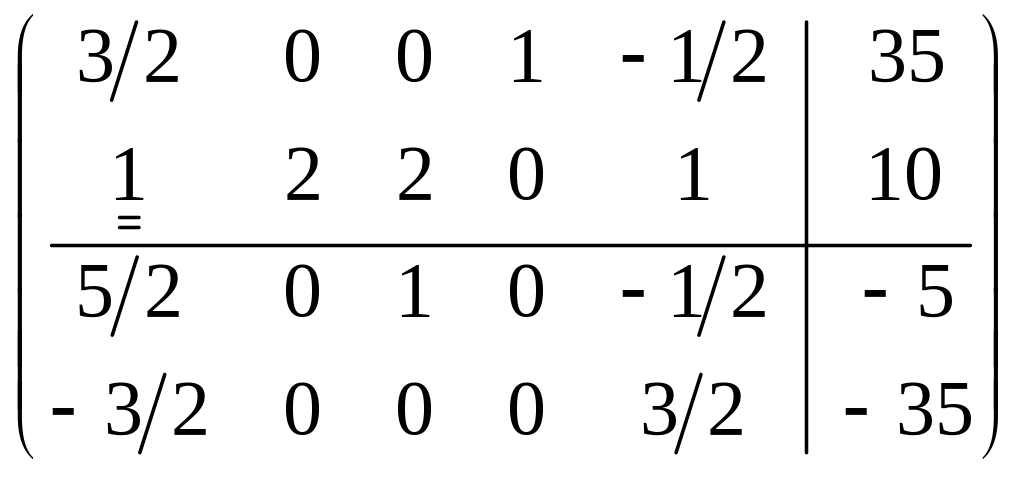
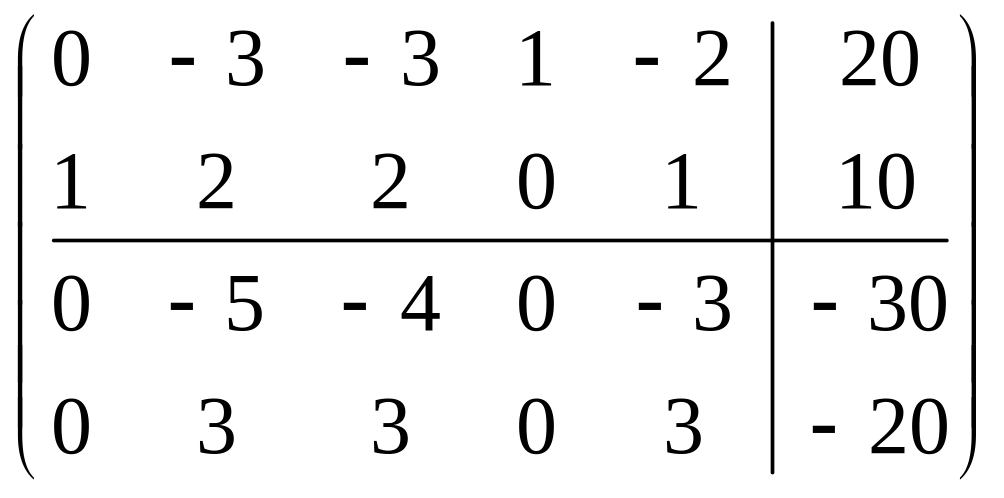Поскольку , все коэффициенты при свободных переменных , и целевой функции будут положительны: , , . Оптимальность достигнута. Причем оптимальный план один: и в нем искусственная переменная . Поэтому по пункту 2 теоремы 3 исходная задача неразрешима (ограничения исходной задачи несовместны). Отметим, что оптимальное значение целевой функции содержит параметр М, что свидетельствует об отсутствии оптимального значения у исходной целевой функции.

Пример 22. Решить методом искусственного базиса задачу ЛП:

;

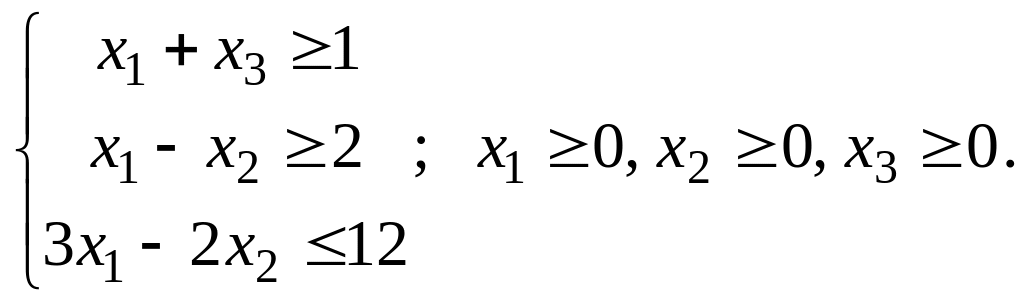
Предварительно приведем задачу к канонической форме, введя балансирующие переменные и перейдя к минимизации

,

Так как с коэффициентом 1 переменная входит только в первое уравнение, а переменная – только в третье уравнение, эти переменные могут быть базисными. Введем еще одну искусственную базисную переменную во второе уравнение, чтобы матрица стала правильной. Тогда -задача имеет вид

;

Расширенная матрица этой задачи записывается следующим образом:

  .

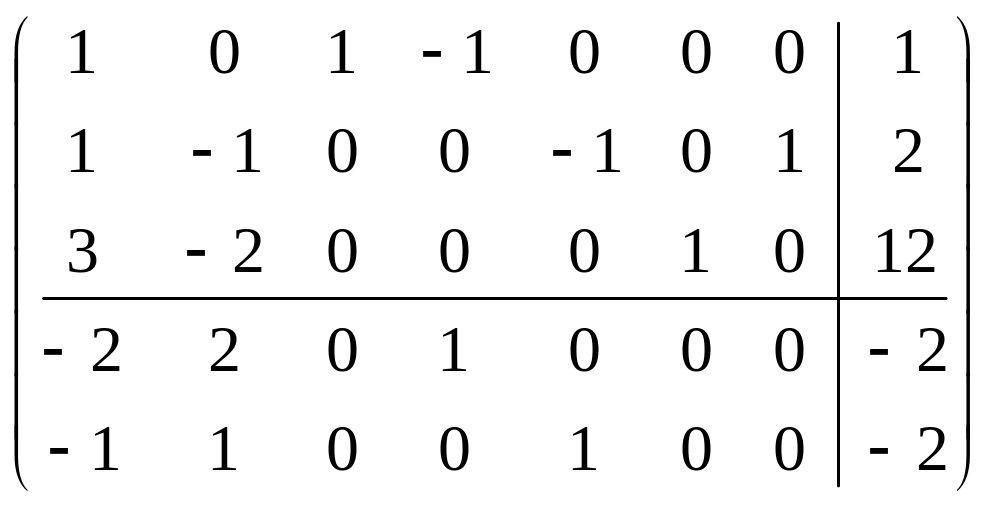Это будет правильная форма -задачи со свободной переменной , в которой коэффициент целевой функции (оптимальности нет). Проведем симплексные преобразования:

  .

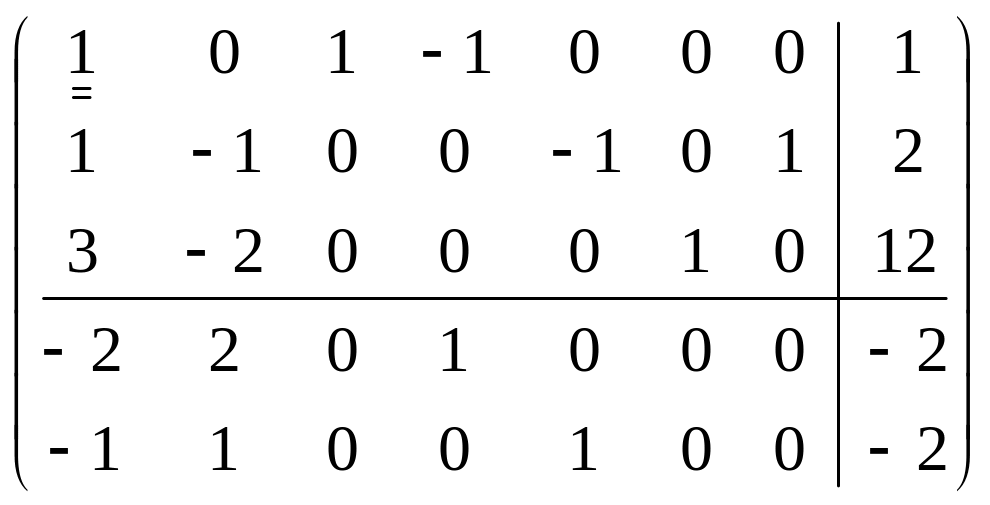
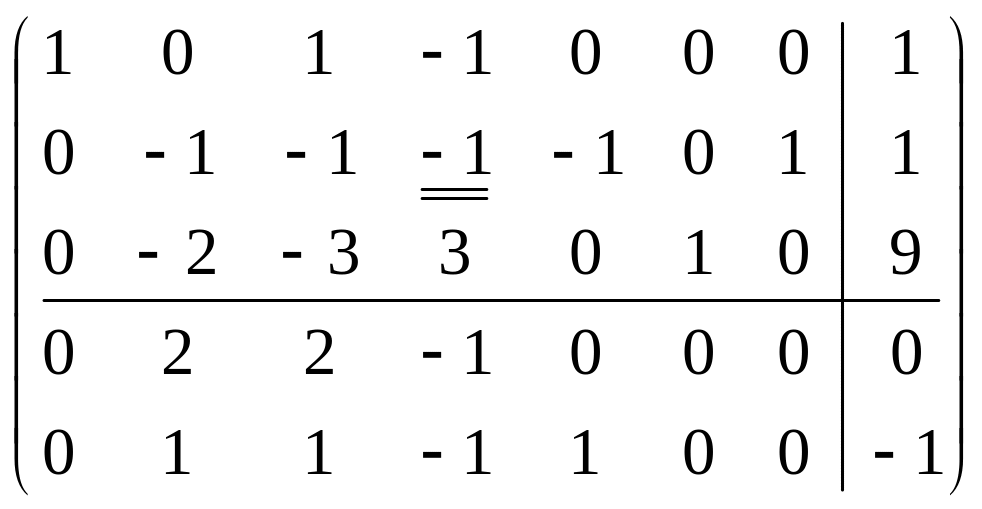
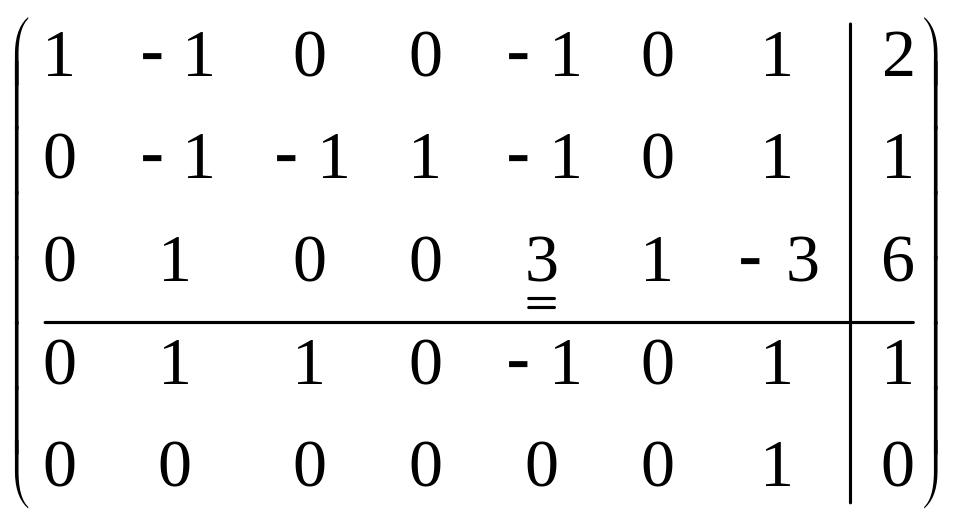
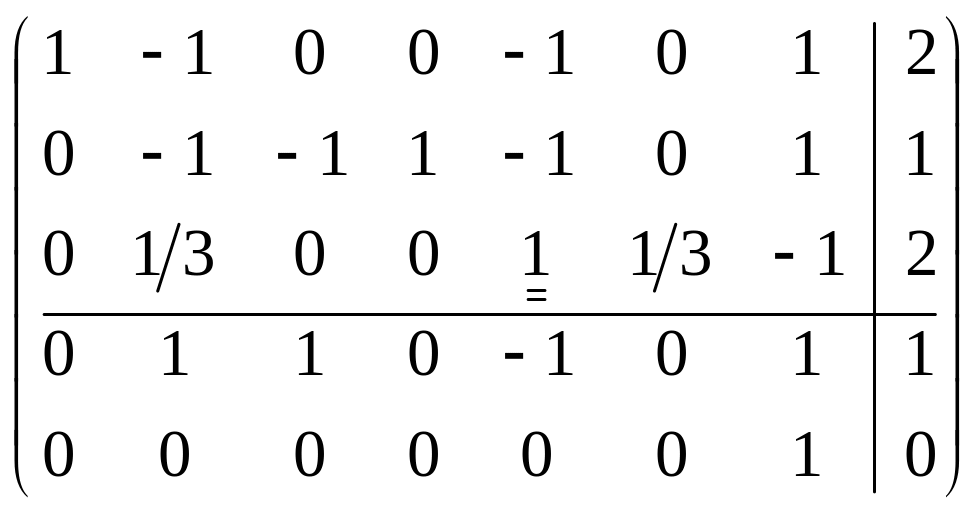
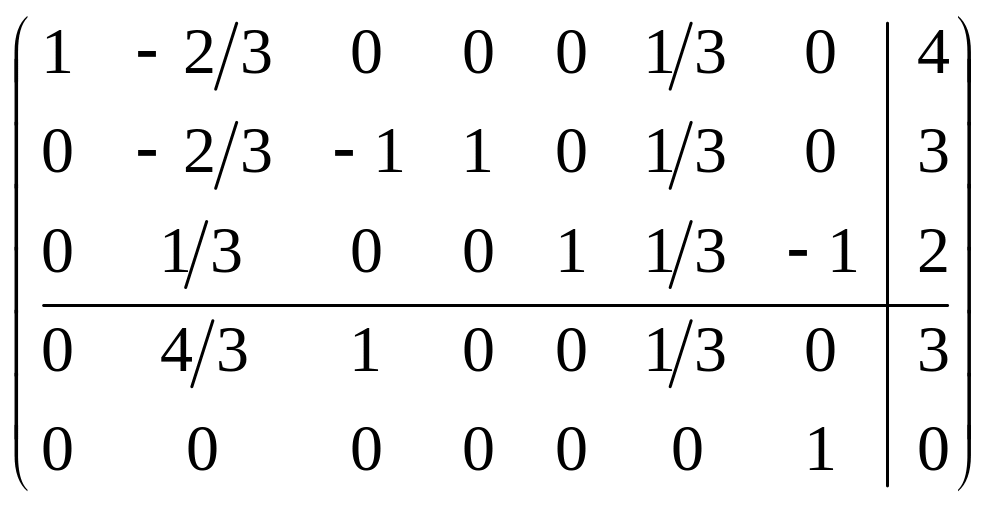коэффициенты при свободных переменных , , , в целевой функции положительны и оптимальность достигнута. Оптимальный план один: . Все искусственные переменные . При этом оптимальное значение и по пункту 1 теоремы 3 оптимальный план (4, 0, 0, 3, 2, 0)  и .