Лекция 15 Граничные условия для 4-3-4-траекторий

Граничные условия для 4-3-4-траекторий показаны на рис. 15.1.

Рисунок 15.1. Граничные условия для 4-3-4-траектории в пространстве присоединенных переменных

Первую и вторую производные рассматриваемых полиномов относительно реального времени можно представить в следующем виде:

(15-1)

;

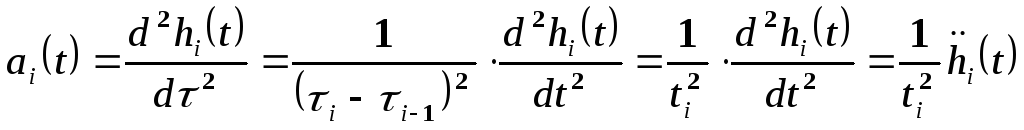, (15-2)

.

Для писания первого участка траектории используется полином четвертой степени:

, . (15-3)

. (15-4)

. (15-5)

1. Для t=0 (начальная точка данного участка траектории). Из граничных условий в этой точке следует:

, (15-6)

. (15-7)

Отсюда имеем и

, (15-8)

что позволяет получить .

Подставляя найденные значения коэффициентов в равенство (15-3), получим:

, . (15-9)

2. Для t=1 (конечная точка данного участка траектории). На этом участке действует условие непрерывности по скорости и ускорению, т.е. скорость и ускорение в конце первого участка траектории должны совпадать со скоростью и ускорением в начале второго участка. В конце первого участка скорость и ускорение соответственно равны:

, (15-10)

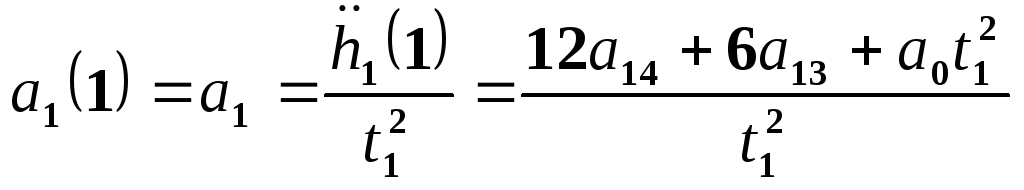. (15-11)

Для описания второго участка траектории используется полином третьей степени:

, . (15-12)

1. Для t=0 (точка ухода). Пользуясь равенствами (9-5) и (9-6) в этой точке, имеем:

, (15-13)

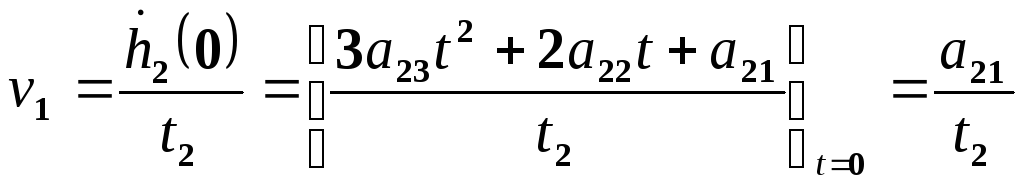. (15-14)

Отсюда следует ,

(15-15)

и, следовательно, .

Поскольку скорость и ускорение в этой точке должны совпадать соответственно со скоростью и ускорением в конечной точке предыдущего участка траектории, то должны выполняться равенства:

и , (15-16)

которые соответственно приводят к следующим условиям:

, (15-17)

или

(15-18)

и , (15-20)

или 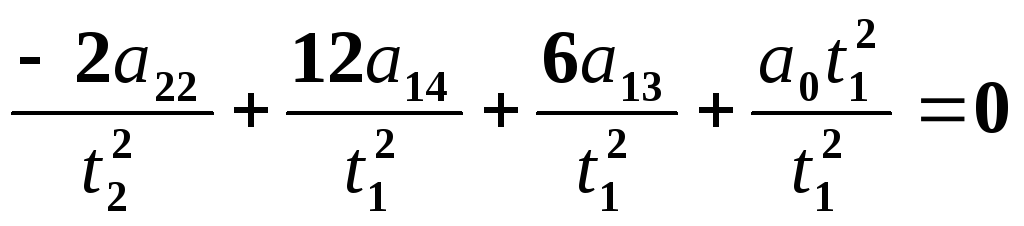. (15-21)

2. Для t=1 (точка подхода). В этой точке скорость и ускорение должны совпасть со скоростью и ускорением в начальной точке следующего участка траектории. Для рассматриваемой точки имеем:

, (15-22)

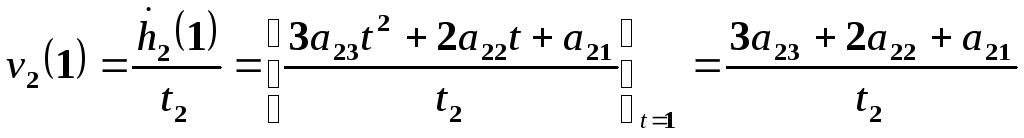, (15-23)

. (15-24)

Для описания последнего участка траектории используется полином четвертой степени:

, . (15-25)

Если в этом равенстве заменить t на и рассматривать зависимость от новой переменной, тем самым мы произведем сдвиг по нормированному времени: если переменная t изменяется на интервале ,то переменнаяизменяется на интервале . Равенство (10-25) при этом примет вид:

, . (15-26)

Пользуясь равенствами (10-1) и (10-2), найдем скорость и ускорение на последнем участке:

, (15-27)

. (15-28)

1. Для (конечная точка рассматриваемого участка траектории). В соответствии с граничными условиями в этой точке имеем:

, (15-29)

. (15-30)

Отсюда следует:

.

Далее,

(15-31)

и, следовательно

.

2. Для 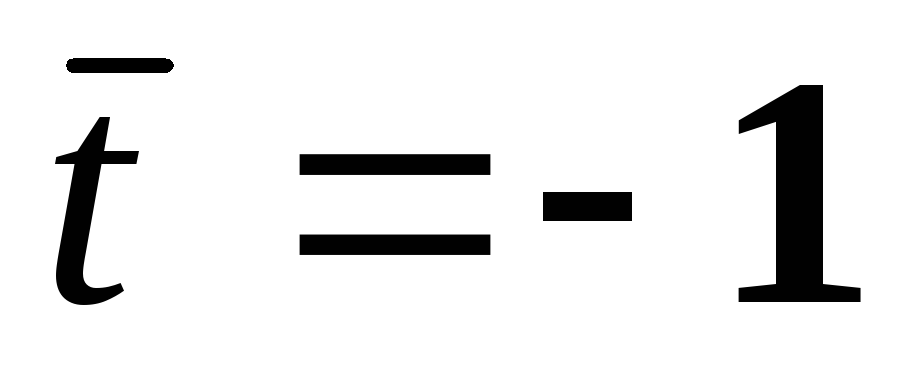(начальная точка последнего участка траектории). Условия непрерывности скорости и ускорения в точке подхода записываются следующим образом:

и , (15-32)

или

(15-33)

и

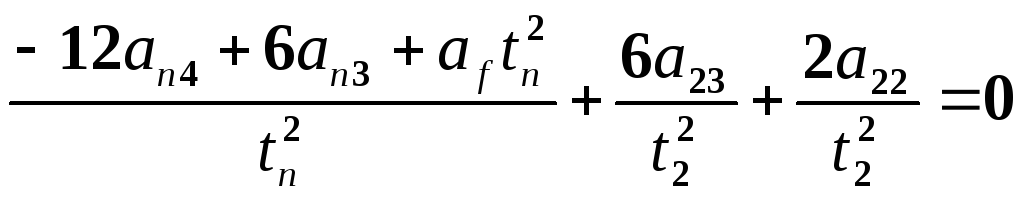. (15-34)

Приращение присоединенной переменной на каждом участке траектории можно найти по следующим формулам:

, (15-35)

, (15-37)

. (15-38)

Все неизвестные коэффициенты в полиномах, описывающих изменение присоединенной переменной, могут быть определены путем совместного решения уравнений (15-35), (15-18), (15-20), (15-37), (15-33) и (15-38). Подставляя эту систему уравнений в матричной форме получим:

, (15-39)

где

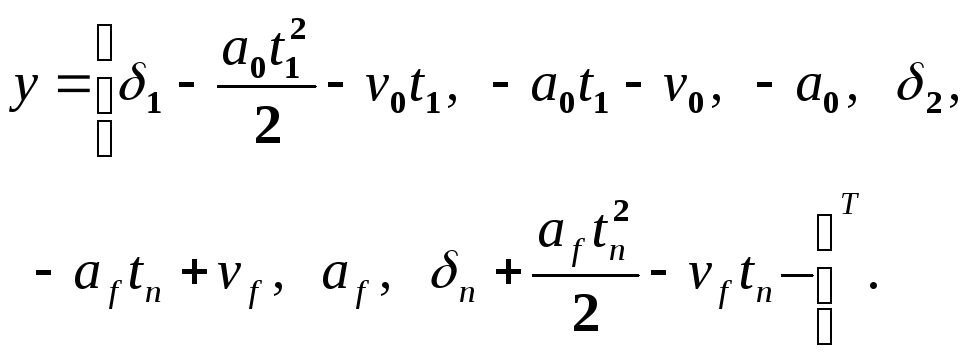(15-40)

, (15-41)

. (15-42)

Таким образом, задача планирования траектории (для каждой присоединенной переменной) сводится к решению векторного уравнения (10-39):

(15-43)

или

. (15-44)

Структура матрицы С позволяет легко найти неизвестные коэффициенты. После определения коэффициентов производим обратную замену, состоящую в подстановке в равенстве (15-26). Тогда получим:

(15-45)

.