
- •Лекция 11 Уравнения Ньютона-Эйлера
- •Вращающиеся системы координат
- •Лекция 12 Подвижные системы координат
- •Кинематика звеньев
- •Лекция 13 Рекуррентные уравнения динамики манипулятора
- •Лекция 14 Планирование траекторий манипулятора
- •Сглаженные траектории в пространстве присоединенных переменных
- •Расчет 4-3-4 - траектории
- •Лекция 15 Граничные условия для 4-3-4-траекторий
Сглаженные траектории в пространстве присоединенных переменных
Планирование сглаженных траекторий в пространстве присоединенных переменных следует проводить с учетом следующих соображений:
В момент поднятия объекта манипулирования движение схвата должно быть направлено от объекта;
Допустимое движение ухода задается на нормали к поверхности, на которой расположен объект, траектория схвата должна проходить через эту точку.
Для участка подхода к заданному конечному положению: схват должен пройти через точку подхода, расположенную на нормали к поверхности, на которую должен быть помещен объект манипулирования.
Траектория движения манипулятора должна проходить через четыре заданные точки: начальную точку, точку ухода, точку подхода и конечную точку (рис. 9.2).
На траекторию накладываются условия:
начальная точка: заданы скорость и ускорение (обычно нулевые);
точки ухода: непрерывность положения, скорости и ускорения;
точка подхода: непрерывность положения, скорости и ускорения;
конечная точка: заданы скорость и ускорение (обычно нулевые).
Значения присоединенных координат должны лежать в пределах физических и геометрических ограничений каждого из сочленений манипулятора.
При определении времени движения необходимо учесть:
время прохождения начального и конечного участков траектории выбираются с учетом требуемой скорости подхода и ухода схвата, и представляет собой некоторую константу, зависящую от характеристик силовых приводов сочленений
время движения по среднему участку траектории определяется максимальными значениями присоединенных скоростей и ускорений каждого сочленения.
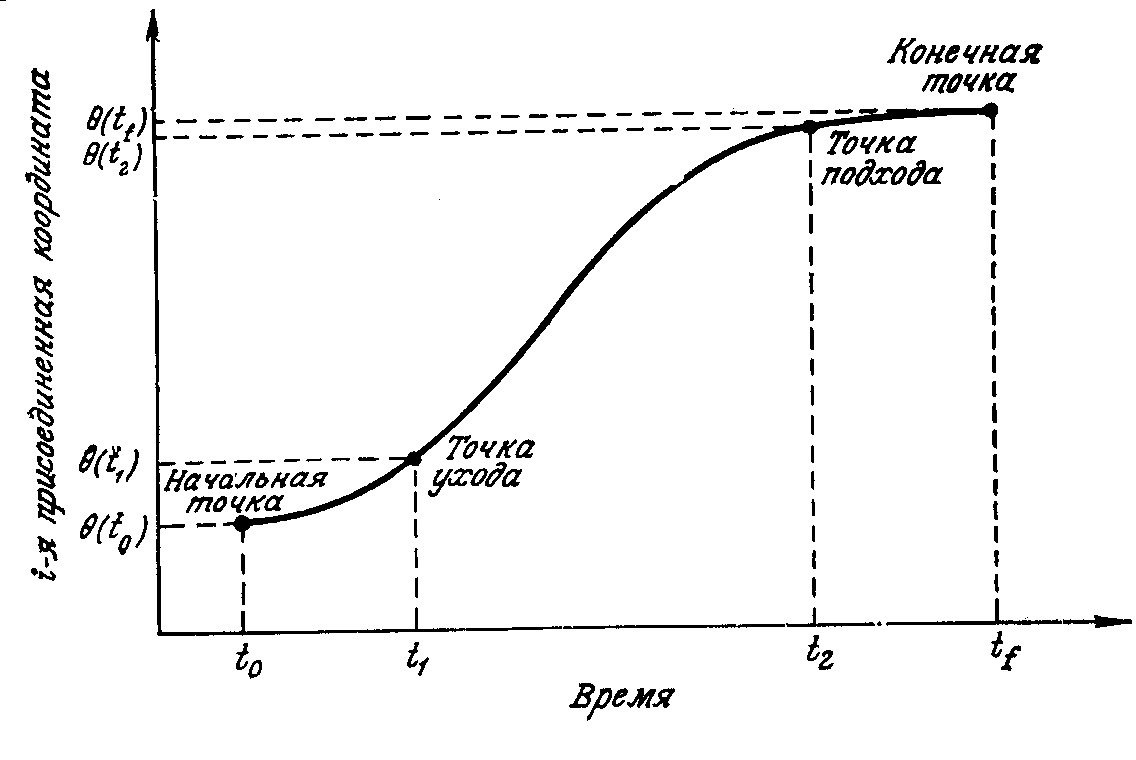
Рисунок 14.2. Ограничения по положению для траектории в пространстве присоединенных переменных
Для проведения интерполяции траектории по заданным узловым точкам нужно выбрать полиномную функцию степени не выше n.
Например, описание i–го сочленения полиномом седьмой степени:
![]() ,
(14-1)
,
(14-1)
в котором неизвестные
коэффициенты
![]() определяются из заданных граничных
условий и условий непрерывности. Однако
полином такой высокой степени трудно
вычислить. Нужно разбить траекторию
движения на несколько участков и
интерполировать каждый участок полиномом
низкой степени.
определяются из заданных граничных
условий и условий непрерывности. Однако
полином такой высокой степени трудно
вычислить. Нужно разбить траекторию
движения на несколько участков и
интерполировать каждый участок полиномом
низкой степени.
Например, траектория изменения каждой присоединенной переменной разбивается на три участка (4-3-4). Первый участок, задающий движение между начальной точкой и точкой ухода, описывается полиномом четвертой степени. Второй (средний) участок – между точкой ухода и точкой подхода – описывается полиномом третьей степени. Последний участок – полиномом четвертой степени.
Расчет 4-3-4 - траектории
Для определения
N
траекторий присоединенных переменных
для каждого участка траектории,
воспользуемся нормированием времени
![]() .
Нормированное время изменяется отt=0
(начальный момент каждого участка) до
t=1
(конечный момент каждого участка).
.
Нормированное время изменяется отt=0
(начальный момент каждого участка) до
t=1
(конечный момент каждого участка).
Обозначения:
t–
нормированное время,
![]() ;
;
![]() - реальное время
(сек);
- реальное время
(сек);
![]() - момент окончания
i–го
участка траектории;
- момент окончания
i–го
участка траектории;
![]() -интервал
реального времени, затраченного на
-интервал
реального времени, затраченного на
прохождение i–го участка траектории;
![]()
![]()
![]() .
.
Траектория
движения j–й
присоединенной переменной задается в
виде последовательности полиномов
![]() :
:
![]() (1-й участок),
(14-2)
(1-й участок),
(14-2)
![]() (2-й участок)
(14-3)
(2-й участок)
(14-3)
![]() (последний участок),
(14-4)
(последний участок),
(14-4)
где i–й коэффициент j–го участка траектории рассматриваемой присоединенной переменной.
Граничные условия выбранной системы полиномов:
Начальное положение =
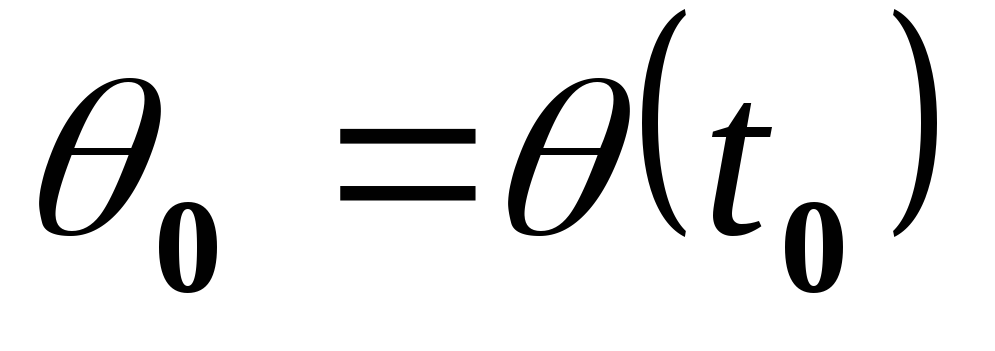 .
.Значение начальной скорости =
 (обычно нулевое).
(обычно нулевое).Значение реального ускорения =
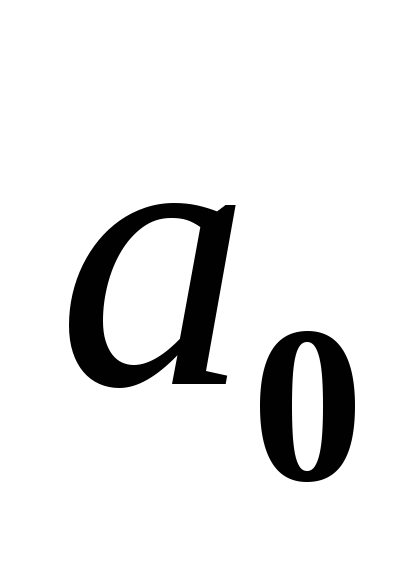 (обычно нулевое)
(обычно нулевое)Положение в точке ухода =
 .
.Непрерывность по положению в момент
 ,
т.е.
,
т.е.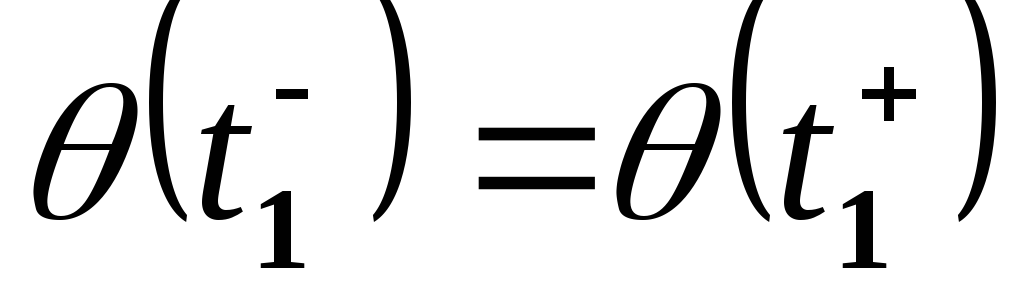 .
.Непрерывность по скорости в момент
 ,
т.е.
,
т.е.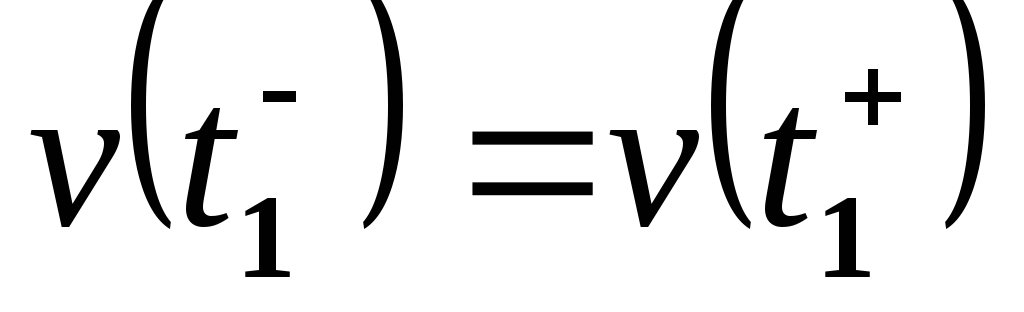 .
.Непрерывность по ускорению в момент
 ,
т.е.
,
т.е.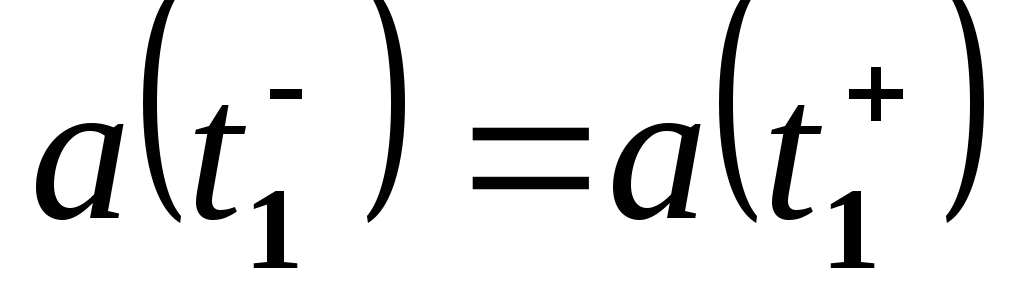 .
.Положение в точке =
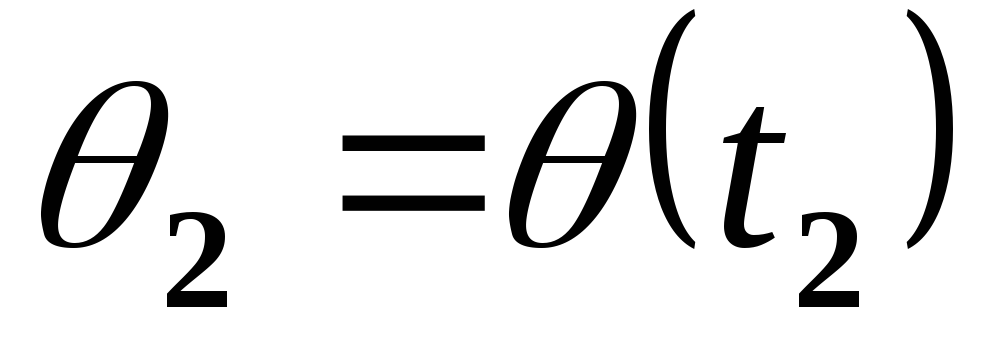 .
.Непрерывность по положению в момент
 ,
т.е.
,
т.е.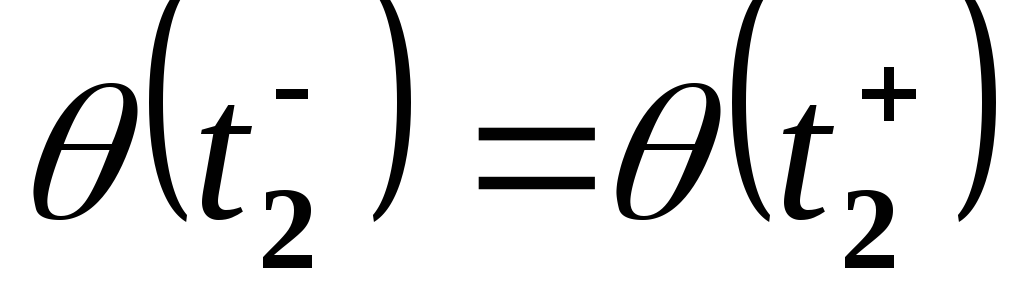 .
.Непрерывность по скорости в момент
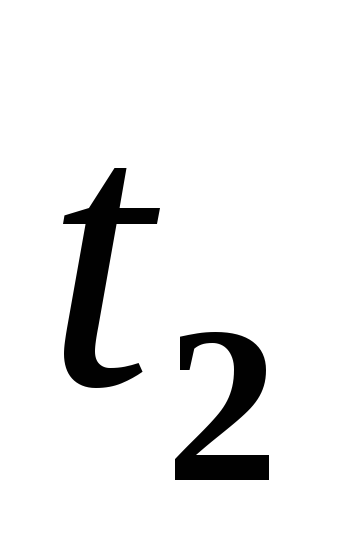 ,
т.е.
,
т.е.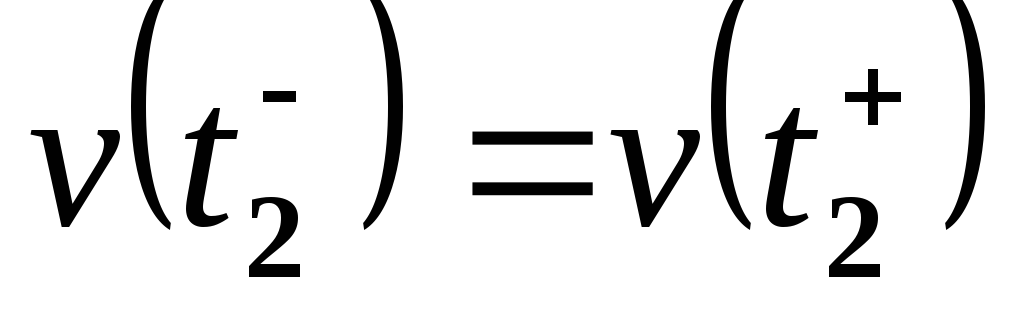 .
.Непрерывность по ускорению в момент
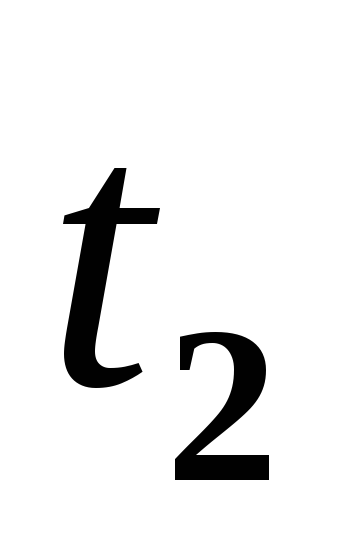 ,
т.е.
,
т.е.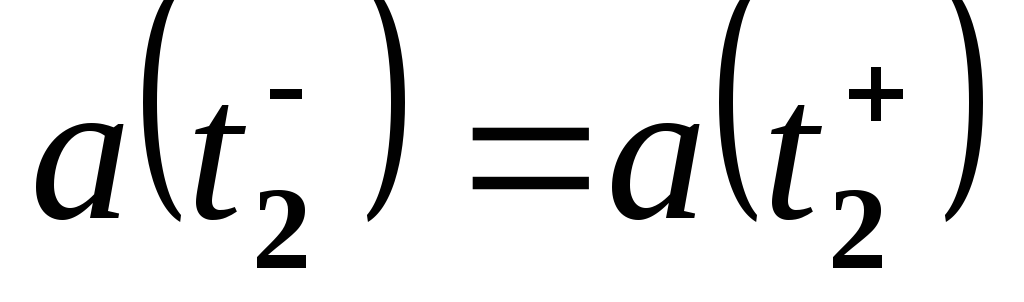 .
.Конечное положение =
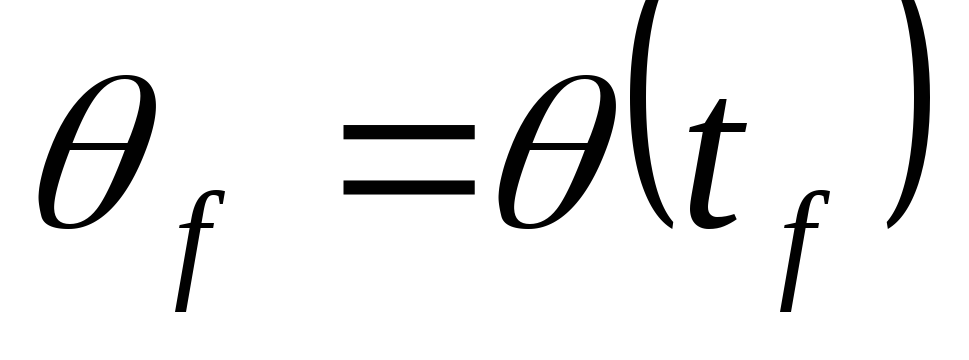
Значение конечной скорости =
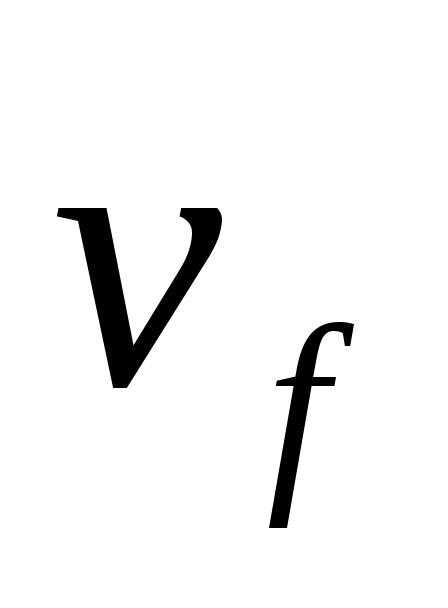 (обычно нулевое).
(обычно нулевое).Значение конечного ускорения =
 (обычно нулевое).
(обычно нулевое).
