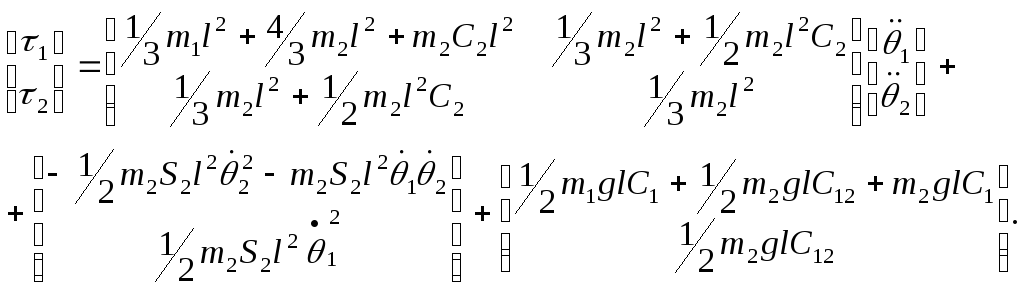Пример: двухзвенный манипулятор

Применение уравнений Лагранжа-Эйлера в форме (6-35) – (6-42) для описания динамики движения манипулятора рассмотрим на примере двухзвенного манипулятора с вращательными сочленениями (рис. 6.3).

Все оси сочленений рассматриваемого манипулятора параллельны оси z, перпендикулярной плоскости рисунка. Физические характеристики, такие, как положение центра масс, масса каждого звена и выбранные системы координат, указаны ниже. Требуется получить уравнения движения рассматриваемого двухзвенного манипулятора, основываясь на равенствах (6-35) – (6-42).

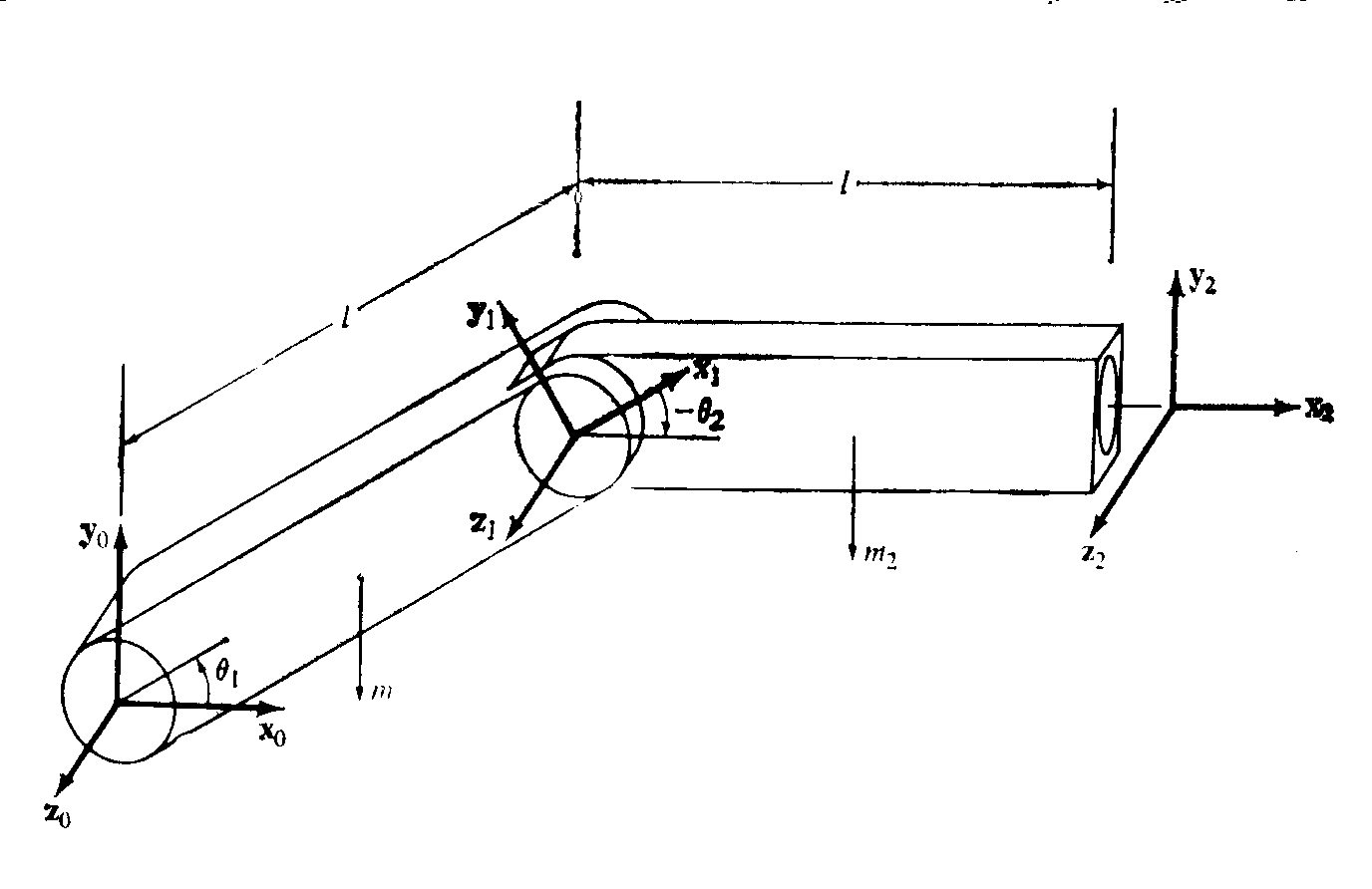
Рисунок 6.3. Двухзвенный манипулятор

Примем:

-присоединенными переменными являются ;

-первое и второе звенья имеют массы и

-параметры звеньев имеют значения ;;.

Тогда для матрицы имеем:

, ,

,

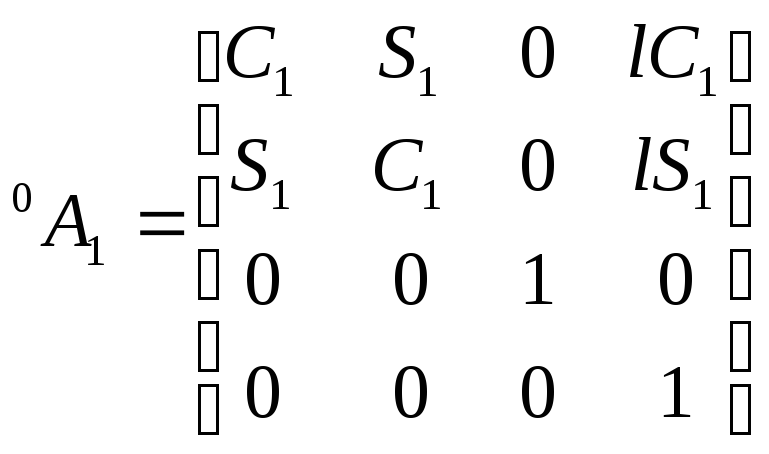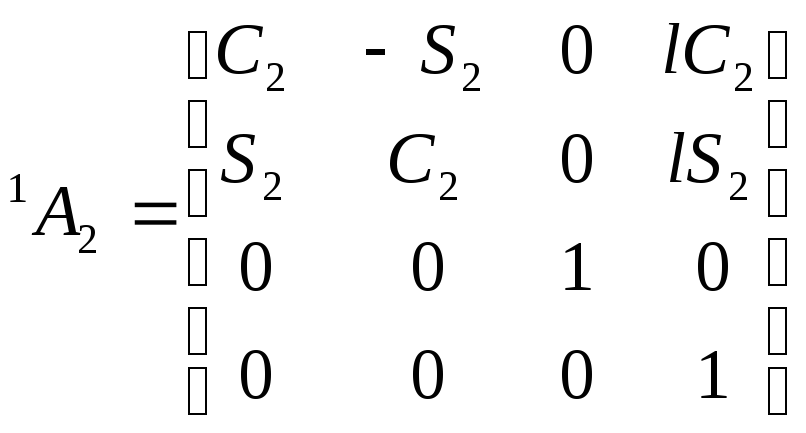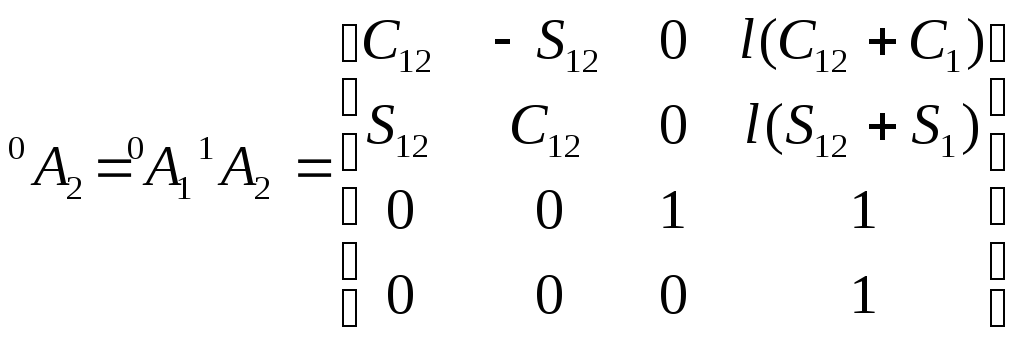где

В соответствии с определением матрицы для вращательного сочленения имеем:

.

Используя выражение (6-19), получаем:

.

Аналогично для иполучаем:

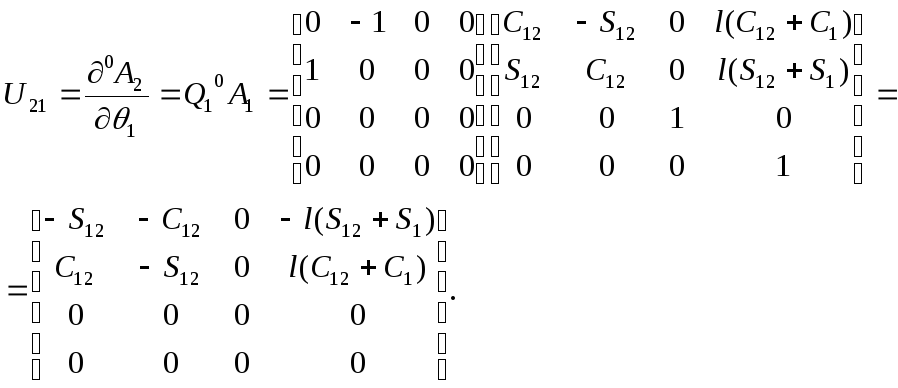
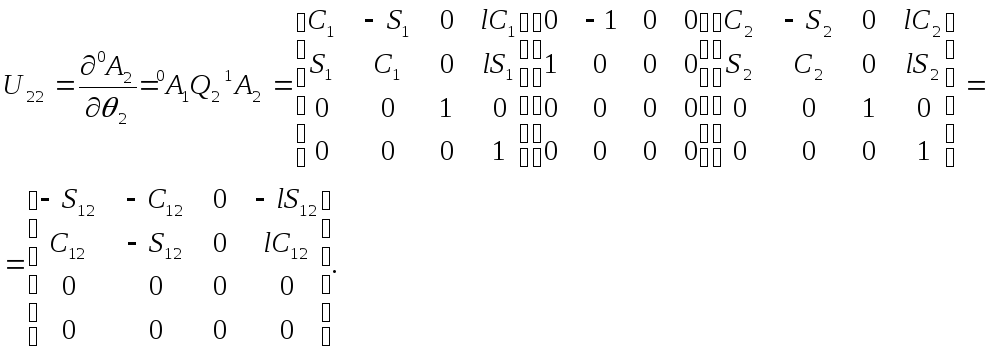
Полагая, что центробежные моменты инерции равны нулю, получим формулу для матрицы псевдоинерции :

; .

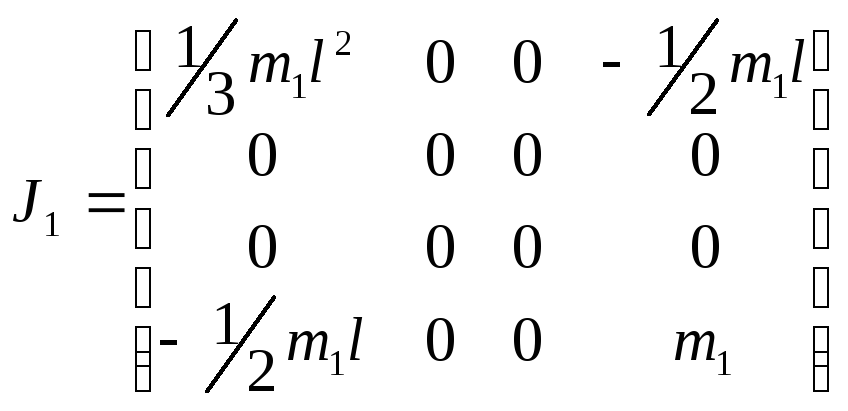Для определения слагаемых, описывающих центробежное и кориолисово ускорение, воспользуемся равенством (6-40). Для i=1 оно дает:

.

С помощью (6-41) можно получить значения коэффициентов . Подставляя их в предыдущее выражение, имеем:

.

Аналогично для i=2:

.

Таким образом:

.

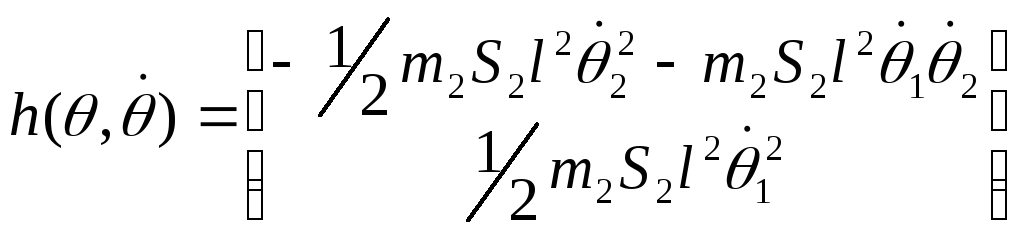Слагаемые, определяющие влияние гравитационных сил :

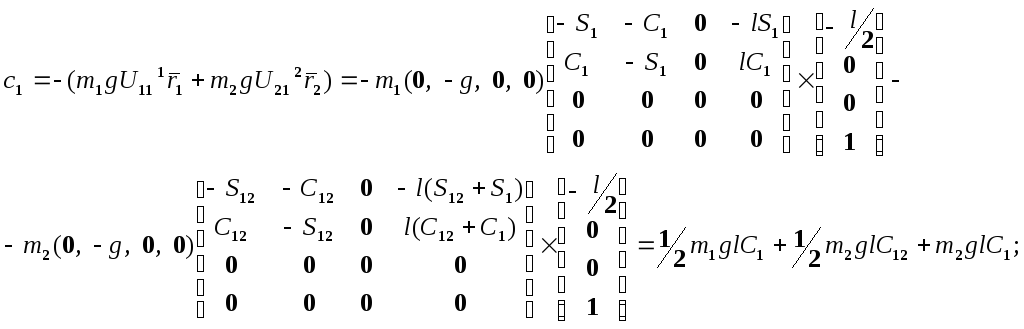
Таким образом, вектор, определяющий влияние силы тяжести:

.

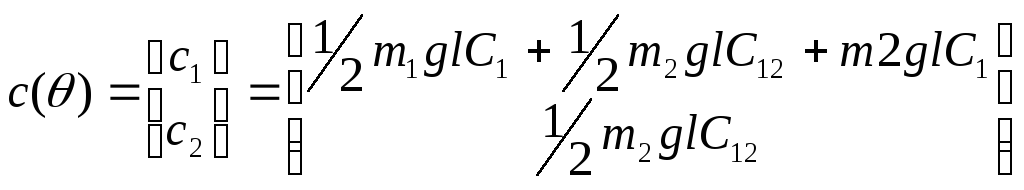Окончательно имеем уравнения описывающие динамику движения двухзвенного манипулятора:

,