Лекция 10 Кинематическая энергия манипулятора

Зная скорость произвольной точки каждого звена манипулятора, найдём кинетическую энергию i-го звена.

Обозначим через кинетическую энергиюi-го звена (i=1, 2, …, n). Пусть кинетическую энергию элемента массыdm i-го звена. Тогда:

. (10-1)

Здесь вместо скалярного произведения используется оператор (след матрицы), что в дальнейшем позволит перейти к матрице инерцииi-го звена.

Подставляя в выражение (10-1) значение из равенства (9-20), получим выражение для кинетической энергии элемента массойdm:

(10-2)

Матрица характеризует положение точкиi-го звена относительно базовой системы координат, обусловленное изменением координаты .

Данная матрица одинакова для всех точек i-го звена и не зависит от распределения массы в этом звене, также как и . Таким образом:

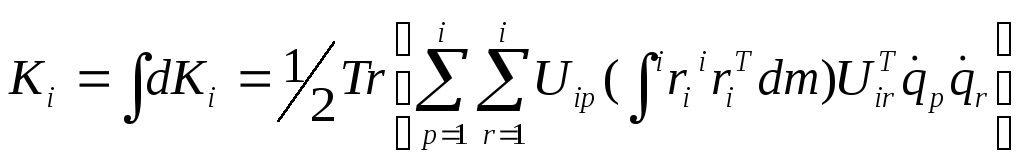. (10-3)

Интегральный член в скобках представляет собой матрицу инерции i-го звена:

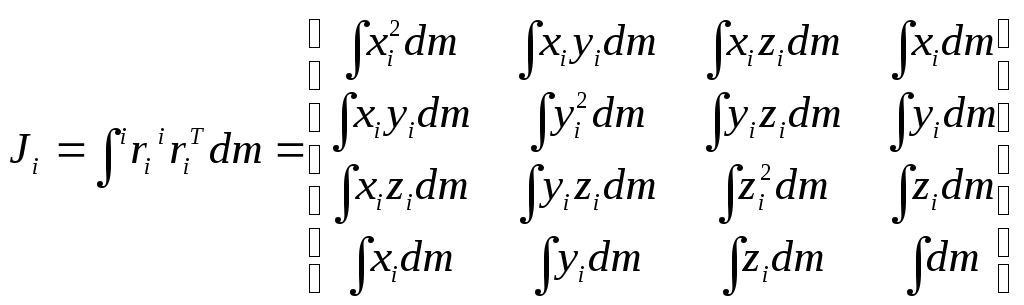. (10-4)

Преобразуя выражения, получим:

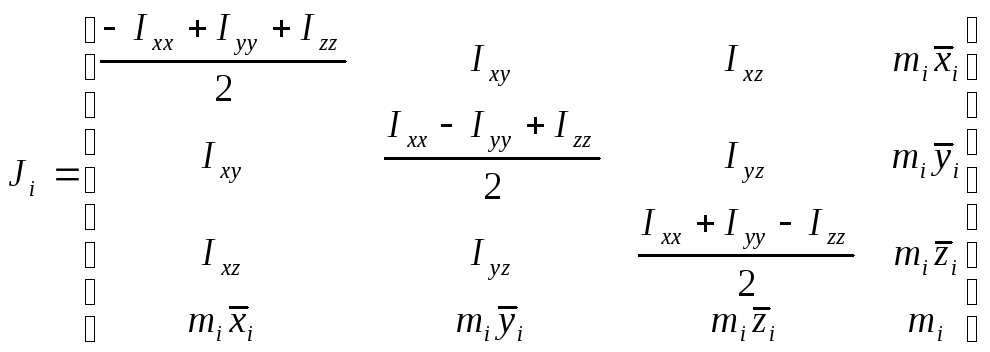, (10-5)

где однородные координаты центра массi-го звена в i-й системе координат;

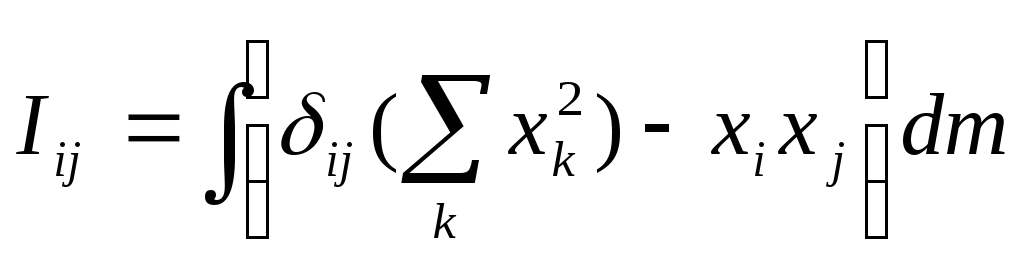- тензор инерции, где i, j, k принимают значения x_i, y_i, z_i (оси i-ой системы координат), а - символ Кроникера.

Формулу (6-26) можно также записать в виде:

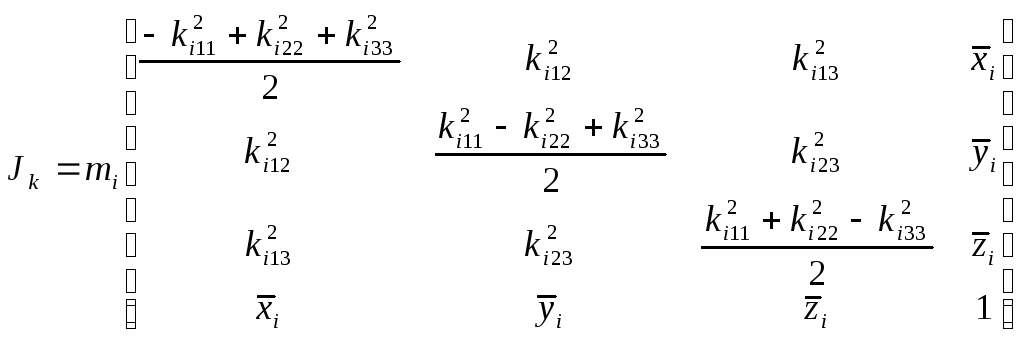. (10-6)

Здесь 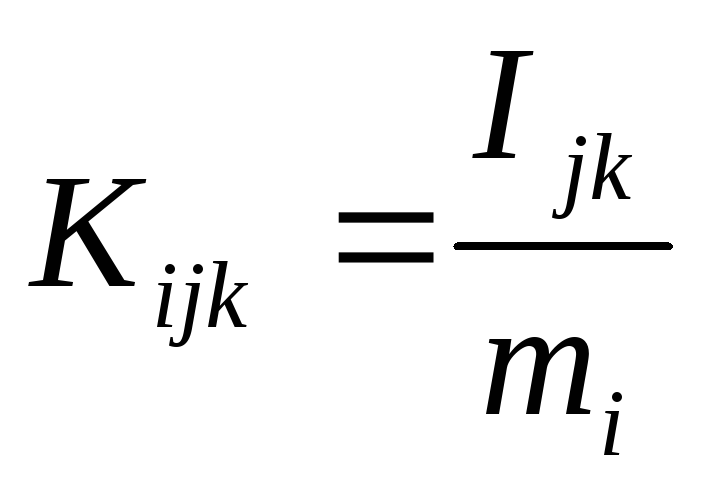иj, k=1, 2, 3, а - радиус вектор центра массi-го звена в системе координат i-го звена. Таким образом, полная кинетическая энергия манипулятора равна:

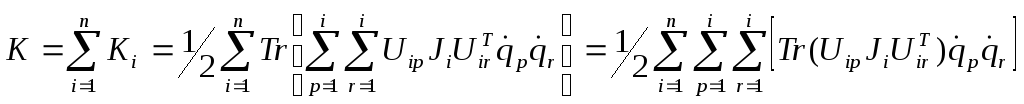. (10-7)

Отметим, что величина J_i (i=1, 2,…, n) зависит только от распределения массы i-го звена в i-й системе координат и не зависит ни от положения, ни от скорости звеньев. Это позволяет однажды вычислив матрицу J_i, использовать полученное значение в дальнейшем для вычисления кинетической энергии манипулятора.

Потенциальная энергия манипулятора

Обозначим полную потенциальную энергию манипулятора через Р, а потенциальную энергию i-го звена – через . Тогда:

. (10-8)

Суммируя потенциальные энергии всех звеньев, получаем:

. (10-9)

Здесь - вектор-строка, описывающая гравитационное ускорение в базовой системе координат. В земной системе координат, аg – ускорение свободного падения на поверхности Земли (g=9,8062 м/с²).

Уравнение движения манипулятора

Используя равенства (10-7) и (10-9), запишем выражение для функции Лагранжа:

. (10-10)

Подставив это выражение в уравнение Лагранжа, получим выражение для обобщённой силы , которую должен развить силовой приводi-го сочленения, чтобы реализовать задание движение i-го звена манипулятора:

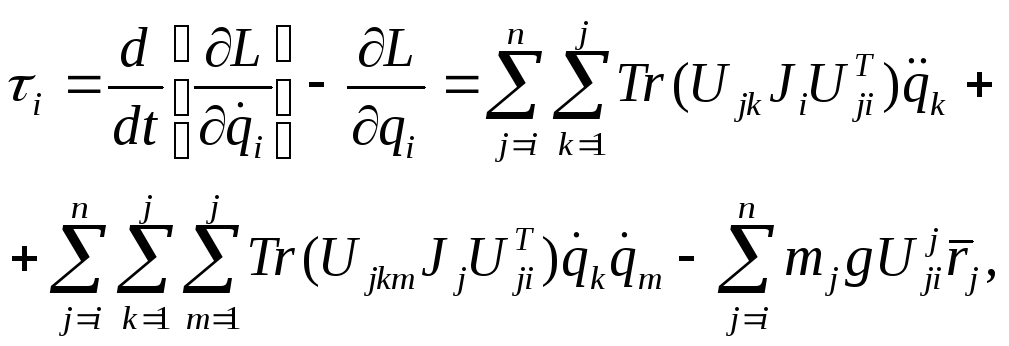(10-11)

.

Выражение (10-11) можно представить в более простой форме:

, , (10-12)

или в матричном виде:

, (10-13)

где - вектор (размерностьюn×1) обобщённых сил, создаваемых силовыми приводами в сочленениях манипулятора:

; (10-14)

- вектор (размерностью n×1) присоединенных переменных манипулятора:

; (10-15)

- вектор (размерностью n×1) обобщённых скоростей:

; (10-16)

- вектор (размерностью n×1) обобщённых ускорений:

; (10-17)

D(q) – симметричная матрица размерностью n×n, элементы которой даются выражением:

, ; (10-18)

- вектор (размерностью n×1) кориолисовых и центробежных сил:

,

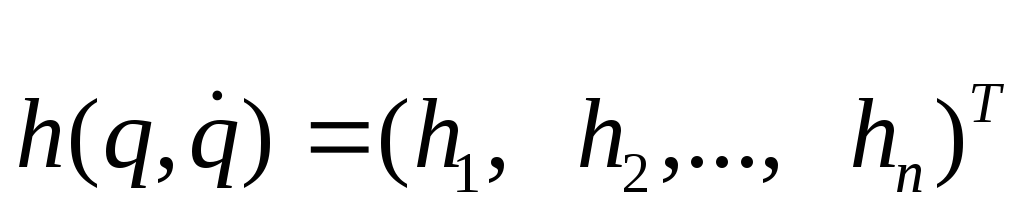, , (10-19)

, ; (10-20)

- вектор (размерностью n×1) гравитационных сил:

,

. (10-21)