1.5 Дискретное преобразование Фурье
Важно понимать, что в вычислительной технике всегда имеет место алгоритм ДПФ, потому что это единственное осуществимое на практике преобразование из семейства преобразований Фурье.
Напомним, что алгоритм ДПФ предполагает преобразование N дискретных отсчетов сигнала во временной области в N комплексных чисел, каждое из которых обозначает некоторую частотную компоненту. С формальными деталями можно познакомиться в теоретическом курсе, а здесь мы попробуем разобраться, как же использовать ДПФ в том, случае, если нам надо просто провести анализ сигнала. Это не так просто, как может показаться сначала, потому что методы ДПФ подразумевают (как мы уже упомянули) использование сложного аппарата функции комплексной переменной, и с ходу, без примеров, порой достаточно сложно интерпретировать полученный результат.
Научимся пользоваться ДПФ и правильно его интерпретировать. Почему это является проблемой? Давайте вспомним, что у нас есть и какова наша цель. У нас есть N дискретных отсчетов некоторого сигнала во временной области. Мы, производя ДПФ, получаем снова N отсчетов, но уже в частотной области и хотим узнать, что же делать, если мы хотим проанализировать частотный состав. Частотный состав чего? Обычно нас интересует не сам дискретизованный сигнал во временной области, а частотный состав исходного непрерывного сигнала, из которого получены отсчеты. Однако тут нас и подстерегает неприятность: мы не знаем, насколько часто мы брали отсчеты при дискретизации. Дискретизованный сигнал – это просто последовательность отсчетов, это функция номера отсчета, и мы не знаем, сколько времени прошло между соседними точками. Когда мы преобразуем эти отсчеты в частотную область, мы по-прежнему не знаем, как соотносится полученный частотный состав дискретизованного сигнала с реальным непрерывным во временной области сигналом. Единственная зацепка – это частота дискретизации. От нее все зависит.
Рассмотрим следующий сигнал:
N= 300; (4)
f=20;
fs=100;
plot ([0:1/fs:N/fs], sin ( [0:1/fs:N/fs] * 2 * pi * f));
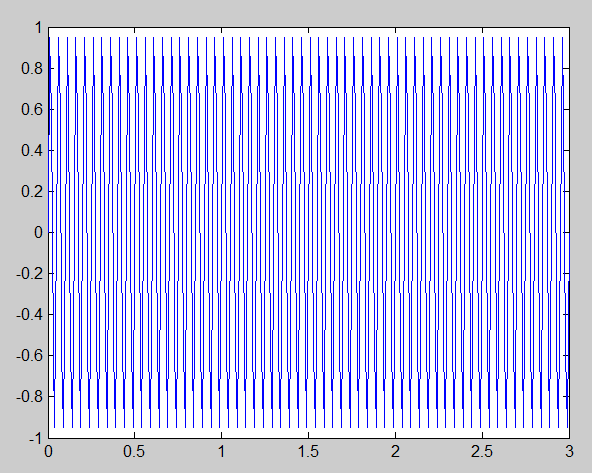
Рис. 4. Результат выполнения команды (4)
Это последовательность, состоящая из N = 300 отсчетов. Дискретизован синус частоты f = 20 Гц. Частота дискретизации fs = 100 Гц.
Следующая запись позволяет с помощью алгоритма быстрого преобразования Фурье найти ДПФ этого же сигнала:
plot (abs (fft (sin ( [0:1/fs:N/fs] * 2 * pi * f)))); (5)
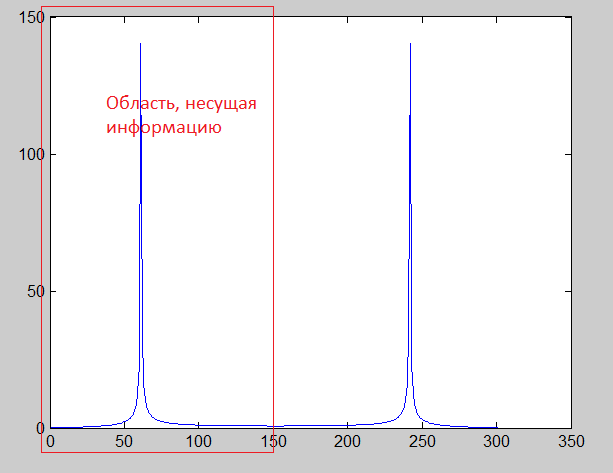
Рис. 5. Результат выполнения команды (5)
Утверждение 3. В случае выполнения условия теоремы Котельникова верно следующее соотношение: f/fs = k/N. Здесь f – частота в Гц, соответствующая k-му отсчету, N – общее количество отсчетов ДПФ. ■
В нашем случае, глядя на частотную область, видим пики, соответствующие k1=60 и k2=240. Посчитаем соответствующие f:
f1 = k1*fs/N = 60 * 100 / 300 = 20 Гц.
f2 = k2*fs/N = 240 * 100 / 300 = 80 Гц.
К сожалению, ДПФ не может различить одинаковые по модулю «положительные» и «отрицательные» частоты. Это значит, что тот же результат, что и при выполнении команды 5, мы бы получили, введя следующее:
plot (abs (fft (sin ( [0:0.01:3] * 2 * pi * (-20)))); (6)
Здесь, говоря терминами ЦОС (с физической точки зрения никаких отрицательных частот конечно не существует), f = -20, что, в соответствии с утверждением 2 раздела 1.4 о неразличимости частот (f + fs*n) означает, что в спектре частота f = -20 начинает периодически повторяться, следовательно, при n=1 f = -20 + 100 * 1 = 80.
Кроме того, из неразличимости «противоположных» частот следует, что график ДПФ является симметричным относительно вертикальной оси в точке нуль.
В общем случае нам нужно анализировать часть графика ДПФ, находящуюся в диапазоне частот [0; f=fs/2], что с учетом утверждения 3 соответствует диапазону отсчетов [0; k=N/2].
Когда хотят упростить описание частотной оси (или оси отсчетов), говорят о «долях частоты Найквиста», fn = fs/2. Тогда рассматриваемый отрезок [0; fs/2] превращается в отрезок [0; 1], и мы можем оперировать с десятичными числами.
Приложение 2. Простейшие присваивания и построение графиков в пакете MATLAB