1.3. Периодическое повторение спектра при дискретизации.

Замечание. Поскольку моделирование производится на компьютере, мы в любом случае имеем дело с квантованными сигналами. Когда мы будем задавать «аналоговую» синусоиду, мы подразумеваем дискретную синусоиду со значительной частотой дискретизации, поэтому ее дискретностью можно пренебречь. ■

Пример, иллюстрирующий замечание.

plot ([0:0.1:2*pi], cos ([0:0.1:2*pi])); (2)

Рис. 1. Результат выполнения команды (2)

Допустим, что некий непрерывный сигнал имеет спектр, показанный синим цветом на Рис. 2. Спектр сигнала, полученного из исходного непрерывного сигнала путем дискретизации с частотой fs, показан ниже на Рис.2. Видим, что из-за появления зеленых «двойников» синего спектра происходит наложение «хвостов», и исходный синий спектр необратимо искажается. Данный рисунок иллюстрирует невыполнение условий теоремы Котельникова. Восстановить исходный сигнал по его спектру не представляется возможным, потому что его спектр изменен. Обратим внимание, что «расползание» «двойников» напрямую зависит от частоты дискретизации fs.

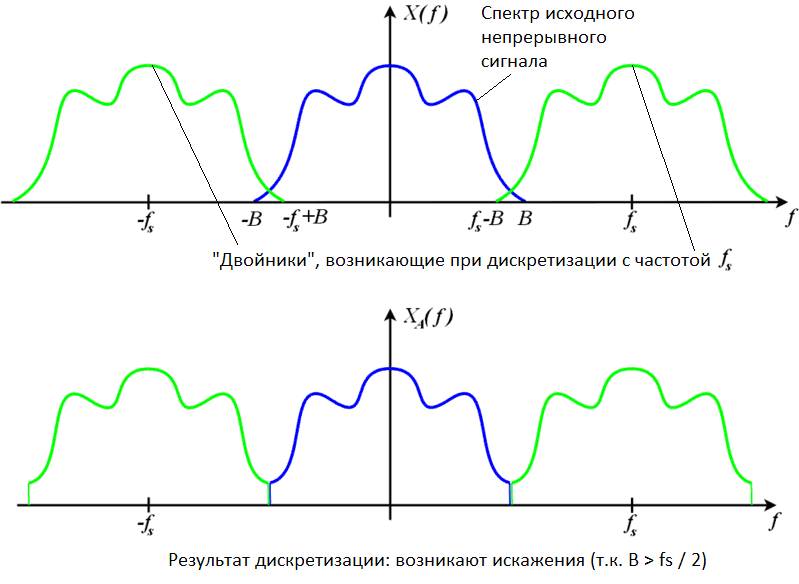
Рис. 2. Необратимые искажения исходного спектра возникают из-за невыполнения условия теоремы Котельникова

Если же условия теоремы Котельникова выполняются, то все копии исходного спектра будут находиться на безопасном расстоянии друг от друга (безопасном от наложения), и тогда исходный спектр не будет искажен.

Приведенное выше объяснение весьма элегантно, но не является доказательным. Существует математический аппарат, «ответственный» за сделанные выше преобразования («размножение», наложения), но мы попытаемся на простом примере продемонстрировать, что же происходит. Для этого в качестве пробного сигнала, подвергающегося дискретизации, будем использовать обычную синусоиду.

1.4 Иллюстрация теоремы Котельникова

Утверждение 2. При дискретизации с частотой fs отсчетов в секунду мы не можем различить дискретизованные значения синусоиды частоты f Гц и синусоиды частоты (f + n*fs) Гц, где n – целое число (положительное или отрицательное).■

Другими словами, при дискретизации любой синусоиды частоты (f + n*fs) Гц мы получим одни и те же отсчеты. Что это значит?

Допустим, была произведена дискретизация некоторой синусоиды и получены отсчеты. Но теперь, если мы захотим по полученным отсчетам понять, какая непрерывная синусоида имелась до дискретизации, то мы получим неоднозначность. Такой непрерывной синусоидой могла быть любая синусоида, имеющая частоту, отличающуюся на n*fs от истинной частоты (т.е. от той частоты, которую имела на самом деле подвергнутая дискретизации синусоида). В итоге мы можем сказать, что через полученные отсчеты проходит любая непрерывная синусоида, отличающаяся по частоте на n*fs от исходной синусоиды. А так как спектр показывает, синусоиды каких частот содержит сигнал (или коротко, какие частоты содержит спектр), то можно сказать, что все эти синусоиды содержатся в спектре дискретизованного сигнала. Мы получили, что спектр дискретизованного элементарного сигнала (т.е. синусоиды) содержит исходную частоту (которую имел этот непрерывный элементарный сигнал) и бесконечное множество частот (своеобразных «двойников»), отличающихся от исходной частоты на n*fs.

Приведенные пояснения иллюстрируют суть теоремы Котельникова применительно к сигналу, содержащему лишь одну частоту. Сама теорема Котельникова имеет дело со всем набором частот исходного сигнала, но суть остается та же. Следовательно, утверждение 2 в некоторой степени облегчает понимание теоремы Котельникова, поскольку фактически из утверждения 2 следует теорема Котельникова.

Теперь приведем пример, иллюстрирующий правильность утверждения 2.Произведем дискретизацию какого-либо синуса, частота которого удовлетворяет условию (f + n*fs), а затем покажем, что через полученные дискретные отсчеты можно провести еще несколько (а в общем случае – произвольно неограниченное число) синусоид, частоты которых удовлетворяют этому же условию, но для других целых n.

plot ([0:0.01:1], sin (2*pi*1*[0:0.01:1])); (3)

hold on

plot ([0:1/3:1], sin (2*pi*1*[0:1/3:1]), 'o');

plot ([0:0.01:1], sin (2*pi*4*[0:0.01:1]));

plot ([0:0.01:1], sin (2*pi*(-2)*[0:0.01:1]));

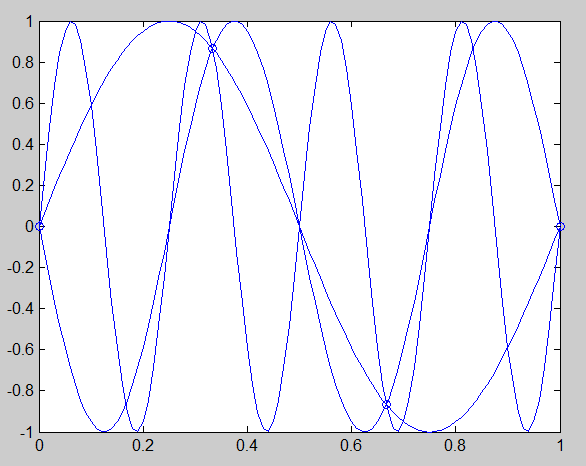
Рис. 3. Результат выполнения последовательности команд (3)

В первой строчке (3) мы изображаем непрерывную синусоиду, в третьей производим ее дискретизацию. Четвертые и пятые строчки показывают, что при восстановлении непрерывной синусоиды по дискретным отсчетам мы не можем однозначно сказать, какую синусоиду мы изначально имели.