3.6.5. Наближені методи розв’язку цілочислових злп.

Існуючі наближені методи розв’язку цілочилених задач лінійого програмування, практичного погляду, більш зручні у застосувані, ніж розглянуті вище метод Гоморі і метод розгалуджень, які умовно можна назвати точними методами оптимізації. Це пов’язано з невиправдано великими витратами часу на розрахунки, тому що ,як правило, економічні задачі мають досить велику розмірність (містять велику кількість змінних і обмежень) і при використанні точних методів кількість обчислень зростатиме з кожним кроком алгоритму. Крім того, іноді, при обрахунку реальних задач досить обмежитися наближеним розв’язком, пошук якого набагато простіший.

Значна частина наближених методів базується на використанні алгоритмів відомих точних методів, таких, наприклад, як метод розгалуджень. До наближених методів належать: метод вектора спаду; різноманітні модифікації точних методів; методи випадкового пошуку та ін.

У загальному випадку наближені методи дають допустимі розв’язки цільчисленої задачі, але не оптимальні. Крім того пошук, допустимого розв’язку цілочиленої задачі наближеним методом в принципі дає практично придатне рішення, але в деяких задачах це рішення може бути досить далеке від оптимального. Тому доцільним є введення критерію ефективності застосування наближених методів, таких як абсолютна і відносна похибки отриманих наближених розв’язків:

- абсолютна похибка,

- відносна похибка;

де Z – значення цільової функції, Х₁— наближений розв’язок, знайдений деяким наближеним методом; Х^* - оптимальний план задачі. Допустимий рівень похибок визначається умовами окремої задачі і якщо обчислена похибка задовольняє цей рівень, допустимий розв’язок задачі вважається оптимальним.

Розглянемо загальну ідею формування наближених алгоритмів розв’язування цілочислових задач, що детально описана в літературі [344566]. Вибирається початковий варіант допустимого плану задачі, потім з ним пов’язується деяка множина альтернативних планів, які утворюють окіл початкового варіанта. Перебором елементів околу здійснюється перехід до кращого альтернативного плану, або приймається локальна оптимальність одного з варіантів. В першому випадку процес покращання плану продовжується, а в другому здійснюється випадковий вибір наступного плану, який беруть за початок пошуку нового оптимального плану. Спосіб визначення і розмір околу та механізм випадкового відбору альтернативних планів залежить від обраного наближеного методу, який також визначає критерій, що фіксує момент закінчення процесу пошуку наближеного розв’язку.

Один з наближених методів розв’язку цілочислених ЗЛП має назву метод вектора спаду [27]. У загальному випадку цей метод дає змогу знаходити локальний мінімум цільової функції, проте, якщо вона має відповідні властивості опуклості, то він приводить до визначення глобального мінімуму [27,899].

Нехай маємо задачу цілочислового програмування (3.19) – (3.21):

; — цілі числа, ( );

Позначимо за R — деякий дискретний точковий простір, тоді множина допустимих планів цілочислової задачі Ω є підмножиною цього простору Ω ( ). Візьмемо дві довільні точки цього простору Х і відстань між ним позначимо через .

З аналітичної геометрії відомо, що відстань між точками у прямокутній декартовій системі координат визначається як довжина вектора тобто , де - відповідно координати точок X та Y у просторі R.

Нехай деякий допустимий план задачі лінійного програмування. Якщо взяти деяке число r>0 то множина всіх точок дискретного простору R для яких виконується нерівність називається відкритим околом з центром у точці і радіусом r, а множина всіх точок для яких виконується нерівність називається закритим околом.

Визначимо деякий окіл R_r1 точки з радіусом r₁, такий, щоб крім плану він містив би інші плани задачі, тоді r₁ має бути не меншим від деякої величини P. Далі розглядатимемо лише зазначені околи планів задачі. Визначимо функцію:

Вектором спаду функції Z(X) у деякому околі R_p довільної точки ( ) називається такий вектор, компонентами якого є величини , де - плани задачі, що належать околу R_p.

Очевидно, що при невід’ємності всіх компонент вектора спаду в околі точки , для будь-яких значень справедливим є твердження:

Нерівність означає, що точка є точкою локального мінімуму функції Z(X) відносно виділеного околу R_p, тобто:

Z(X') = min [Z(X)]

Для від’ємних компонент вектора спаду будуть нерівність означає, що не є точкою локального мінімуму в зазначеному околі. Точка виділеного околу, для якої різниця буде найменшою, визначає напрям найшвидшого спаду цільової функції Z(X) ( ). Цей очевидний факт і лежить в основі обчислювального алгоритму методу вектора спаду.[66778]

Процес пошуку розв’язку цілочислової задачі методом вектора спаду є послідовним перебором точок (допустимих планів), що зменшують значення цільової функції. Спочатку визначаються компонент вектора спаду для деякої початкової точки. Якщо всі вони невід’ємні, то цю точку вважають точкою локального мінімуму, в протилежному випадку знаходимо центр нового околу (нову точку) і перевіряємо його компоненти на невід’ємність.

Як правило, для кожного нового околу не потрібно обчислювати всі компоненти вектора спаду, а лише частину з них, що значно скорочує об’єм і тривалість обчислень.

Алгоритм реалізації методу вектора спаду включає виконання наступних кроків:

1. Обирається початкова точка Х₀ і радіус околу r так, щоб точка Х₀ була допустимим планом відповідної задачі цілочислового програмування 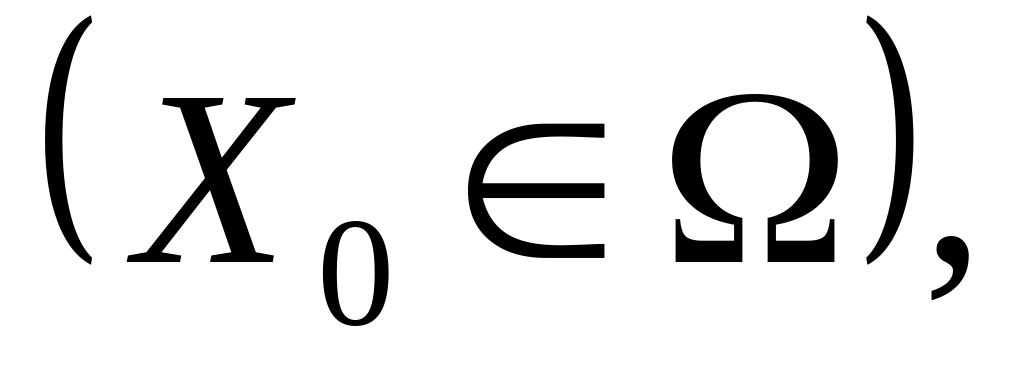а окіл містив також і інші допустимі плани задачі. Вибір Х₀ здійснюється випадково, але з обов’язковою перевіркою виконання зазначених умов.

2. Визначаються компоненти вектора спаду у обраному околі. Якщо всі його компоненти невід’ємні, то точку локального мінімуму знайдено, задача розв’язана і оптимальним цілочисловим планом є .

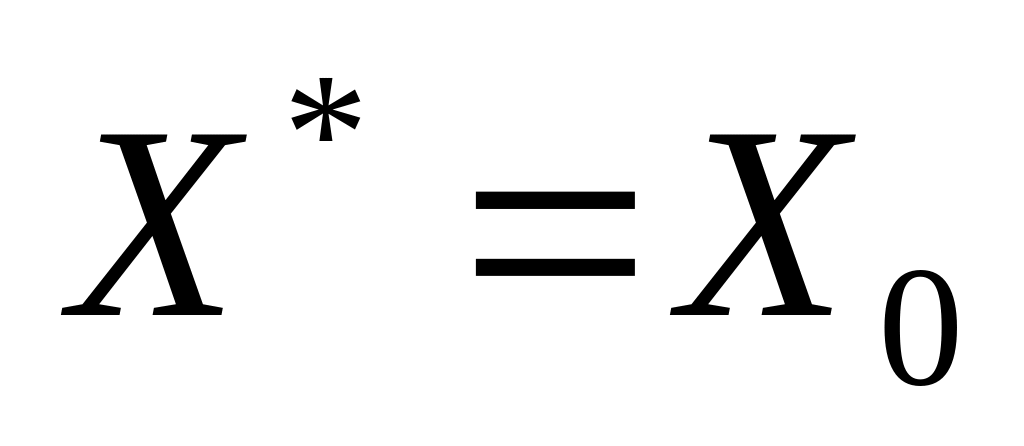3. Якщо деякі компоненти вектора спаду не задовольняють умову невід’ємності, то вибираємо компоненту 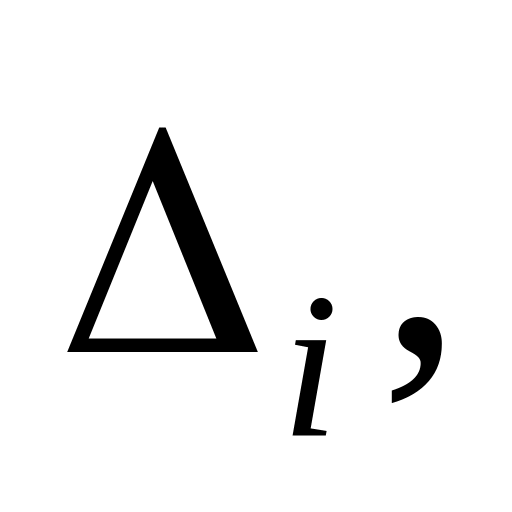яка має найменше значення і визначає точку , що зменшує значення цільової функції і ця точка приймається за центр нового околу.

4. Повторення дій пункту 2.

5. Розрахунки продовжуються доти, поки для деякої точки всі компоненти відповідного вектора спаду не будуть задовольняти умову невід’ємності.

Приклад 3.7. Розв’яжемо цілочислову задачу з прикладу 3.6. методом вектора спаду.

Розв’язок.

Нехай Обрана точка є допустимим планом задачі, оскільки задовольняє всі обмеження і умову цілочисловості, а окіл обраного радіусу містить інші плани задачі, наприклад, точку .

Визначаємо точки, які належать означеному околу: (рис. 3.8.).

Визначаємо компоненти вектора спаду, ввівши такі позначення:

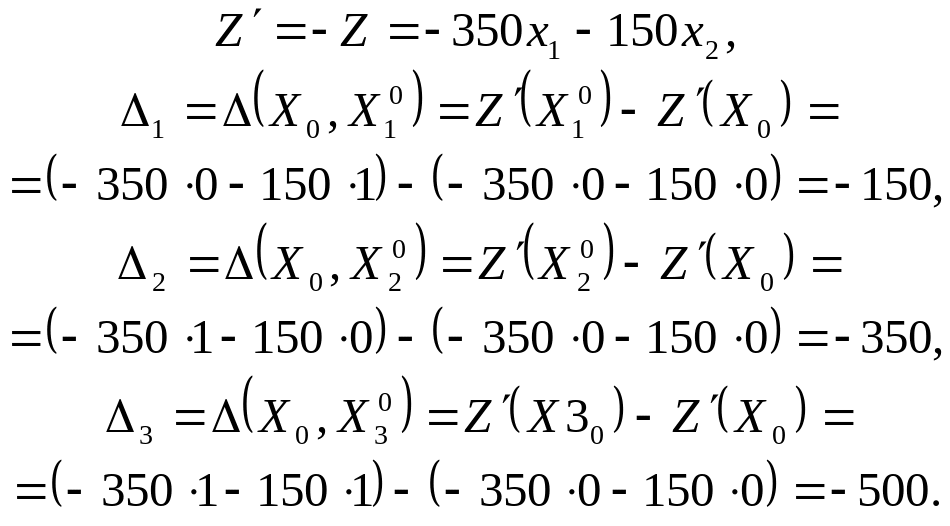
Найменшою є третя компонента вектора спаду, отже, відповідна їй точка стає центром наступного околу Радіус r =3,5

У новий окіл будуть входити точки з координатами:

Необхідно обчислити значення компонент вектора спаду для обраних точок.

Д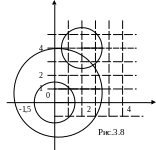 ля трьох точок потрібні величини були розраховані на попередньому кроці, тому залишається обчислити компоненти вектора решти точок.

Після проведення обчислень маємо, що найменшого значення набуває компонента вектора, яка відповідає точці тому наступний цент околу переміщається в нову точку Нехай

Виконуємо розрахунки компоненти вектора спаду лише для двох точок околу, бо решта точок є спільними з точками попереднього кроку:

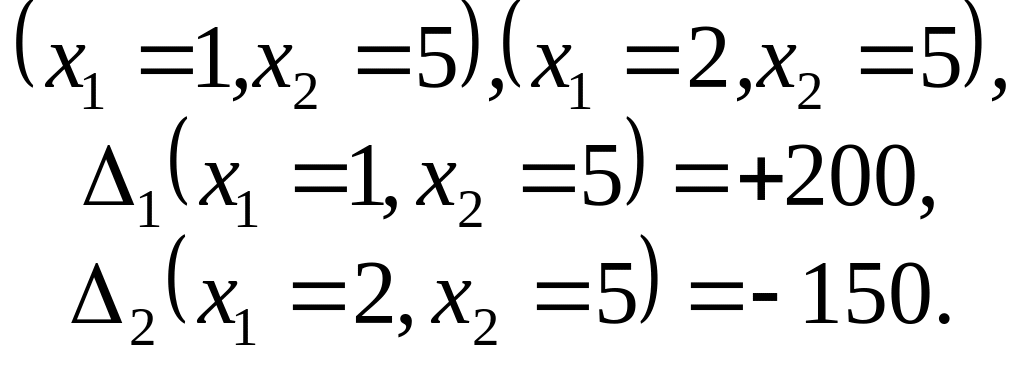
Порівнюючи ці значення, визначаємо точку нового центру околу з радіусом r =1 Компоненти вектора спаду в цьому околі набувають тільки додатних значень. Отже, процедуру наближення завершено, і ця точка є оптимальним планом цілочислової задачі: X*= (x₁=2;x₂=5); Zmax = 1450.

Примітка: метод вектора спаду може бути застосований і для розв’язку цілочислових нелінійних задач.