Практическая работа № 3

ОЦЕНКА ТОЧНОСТИ ФУНКЦИИ НЕЗАВИСИМЫХ ИЗМЕРЕННЫХ ВЕЛИЧИН

Цель работы : освоить методику нахождения средней квадратической погрешности функции независимых измеренных величин.

Методические указания

Некоторая величина y вычисляется как функция независимых измеренных величин

(3.1)

Средние квадратические погрешности измеренных величин l₁,l₂‚..,l_k известны и равны соответственно m₁,m₂,...,m_k.

Тогда средняя квадратическая погрешность функции выражается формулой

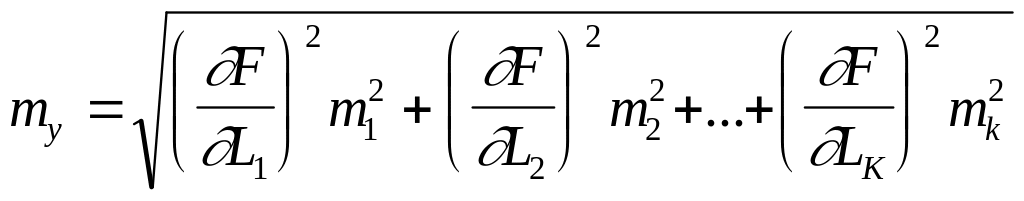(3.2)

где - частные производные рассматриваемой функции по всем измеренным величинам.

В частном случае, когда величина Y представляет собой линейную функцию измеренных величин вида

( 3.3)

ее средняя квадратическая погрешность выражается формулой

( 3.4)

где - коэффициенты линейной функции.

Если величина Y представляет собой алгебраическую сумму измеренных величин

(3.5)

то ее средняя квадратическая погрешность определяется по формуле

(3.6)

При m₁=m₂=...=m_k=m получим

(3.7)

П Р И М Е Р

Превышение при тригонометрическом нивелировании вычисляется по формуле

h=lsind+n-i

где l- измеренная наклонная длина;

d- угол наклона;

n и i - высоты сигнала и инструмента,

Найти среднюю квадратическую погрешность определения превышения, если при измерении были получены следующие результаты:

l= 38,753м; mм; d = 28 12’30”; m = 30”;

i= 0,584; m= 0.002м; n = 0.621; m= 0.002м.

Воспользуемся для вычисления формулой (3.2)

Следует обратить внимание на важную особенность. Если по погрешности угловой величины вычисляется погрешность линейной величины, то угловая погрешность должна быть выражена в радианах. В рассмотренном примере на основе погрешности угла наклона m вычисляется погрешность линейной величины- превышения. Поэтому погрешность переведена в радианную меру делением на r= 206265”.

Задачи для самостоятельного решения

3.1. При прокладке полигонометрического хо- да по наклонной выработке горизонтальное проложение сторон определяется по формуле

l ₀ = lcosd ,

где l- измеренная наклонная длина; d- угол наклона.

Найти среднюю квадратическую погрешность определения горизонтального проложения, если при измерении были получены следующие результаты:

l = 38,120м ; m_l = 0.003м; d= 25 43’00”; m_ = 45”.

3.2. От исходного репера А, отметка которого определена ранее со средней квадратической погрешностью m_исх = 6мм, проложен ход геометрического нивелирования из n = 30 станций к реперу В. Превышение на каждой станции определялось по красной и черной сторонам рейки и за окончательное его значение принималось среднее. Считая среднюю квадратическую погрешность отсчета по рейке равной m₀ = 2мм, найти среднюю квадратическую погрешность определения отметки репера В.

3.3. Горизонтальное проложение линии может определяться по формуле

l₀=l-(h²/2l)

где l - измеренная наклонная длина;

h - превышение между концами линии.

Найти среднюю квадратическую погрешность определения горизонтального проложения, если

l =48,251м; m = 0.004м; h = 1.016м; m = 0.002м.

3.4. При лбработке длин в подземной полигонометрии поправка за температуру вычисляется по формуле Dl =0.0000115l(t-t)

где l - измеренная длина;

t - температура измерения;

t₀ - температура компарирования.

Найти среднюю квадратическую погрешность определения поправки за температуру для длины l= 100.208, если при измерении длины температура была зафиксирована со средней квадратической погрешностью m_t =2°,а при компарировании- с погрешностью m_t0 = 1°.

3.5. При производстве гироскопического ориентирования дирекционный угол ориентируемой стороны вычислялся по формуле

a = a +G -G +dg

где a - дирекционный угол исходной стороны на поверхности , известный с погрешностью m_исх =5”;

G и Г - гироскопические азимуты исходной и ориентированной сторон, определенные как среднее из 4-х определений Г и 2-х определений Г;

dg - поправка за разность сближений меридианов, определяемая практически без погрешности.

Найти среднюю квадратическую погрешность определения дирекционного угла гирокомпасом, если средняя квадратическая погрешность одного определения гироскопического азимута m = 20”.

3.6. Найти среднюю квадратическую погрешность вычисленной площади трапеции, если непосредственно измерены основание a = 15.45м с m_а = 0.03м, основание b = 24.13м с m_b = 0.05м, высота h = 110.43м с m_h = 0.03м.

3.7. От стороны , дирекционный угол которой получен из геометрического ориентирования со средней квадратической погрешностью m_геом = 45”, проложен теодолитный ход из 25 углов к стороне , ориентированной гирокомпасом со средней квадратической погрешностью m_гир = 20”.

Найти среднюю квадратическую величину угловой невязки в ходе, если углы измерялись с погрешностью m_ =20”.

3.8. В треугольнике АВС непосредственно измерены сторона С= 113.00м с погрешностью m_с = 0.07м и углы А = 62°19’ с погрешностью m_а = 1’ и В= 48°32’ с погрешностью m_в =2’. Найти среднюю квадратическую погрешность вычислений стороны a.

3.9. Определить, с какой точностью необходимо измерять горизонтальные углы в подземном теодолитном ходе, чтобы получить среднюю квадратическую погрешность дирекционного угла 16-й стороны , равную 60”(углы измерены равноточно, погрешностью дирекционного угла исходной стороны пренебречь).

3.10. Расстояние между двумя точками с известными координатами определяется по формуле l=(y/sin),

причем DU= 108.764м и a= 20°22’00”. Считая, что величины DU и a найдены без погрешности, а sina определен по пятизначным таблицам со средней квадратической погрешностью m=0.000003,найти среднюю квадратическую погрешность вычисления длины l.

3.11. В равностороннем треугольнике измерена сторона a= 100.00м с погрешностью m = 0.05м. Найти среднюю квадратическую погрешность вычисляемой площади треугольника в абсолютной и относительной мере.

3.12. В подземном теодолитном ходе измерено n= 15 углов со средней квадратической каждого равной m=20”. Дирекционный угол исходной стороны определен с погрешностью m =25”.

Найти среднюю квадратическую погрешность дирекционного угла последней стороны теодолитного хода.