2.Прокладка двух ходов в одном направлении

Обработка измерений приведена в табл.2.

При этом получены

[d]=-21 [½d½]=275

фактическое значение критерия составило

что существенно меньше допустимого значения.

Таким образом, критерий не выявил систематических погрешностей, хотя они в измерениях присутствуют. Это следовало ожидать, так как систематическая погрешность одинакова при первом и втором измерениях и исключается из их разности.

Поскольку систематические погрешности не выявлены, среднюю квадратическую погрешность измерения угла вычисляем по формуле

и далее находим погрешность окончательного значения

При вычислении окончательного значения из выражения

систематическая погрешность каждого измерения в неизменном виде переходит в среднее значение. Поэтому полученная погрешность m_ок =12”.6 является приуменьшенной и не отражает реальной точности.

Соответсвенно, средняя квадратическая погрешность дирекционного угла последней и не отражает реальной точности.

Соответственно, средняя квадратическая погрешность дирекционного угла последней стороны

отражает только случайные погрешности.

В действительности дирекционный угол содержит еще и систематическую погрешность

m_{a12(сист)} =-7”.12=-84”

Таким образом при втором способе прокладки хода имеющиеся систематические погрешности не выявлены, не исключены из окончательных результатов и не учтены при оценке точности, которая по этой причине не является объективной.

2. Оценка точности при наличии систематических погрешностей

Для типичных систематических погрешностей, которые встречаются в маркшейдерско- геодезических измерениях, установлены их закономерности. Это позволяет в значительной мере нейтрализовать указанные погрешности введением соотвествующих поправок (например, за компарирование, температуру, провес при рулеточных измерениях).

Поправки определяются с неизбежными погрешнотями.Они переходят в результаты измерений и являются теми остаточными погрешностями, исключить которые уже невозможно. Существенно, что сама по себе погрешность определения поправки является случайной и характеризуется средней квадратической величиной m_q . Однако, из-за введения поправки сразу во множество измерений ее погрешность для совокупности измерений становится истематической.

Таким образом, окончательный результат решаемой задачи находится как функция измеренных величин, которые содержат не тольо случайные, но и остаточные систематические погрешности. При оценке точности этой функции влияние случайных погрешностей оценивается как обычно. Нахождение ее погрешности, обусловленной остаточными систематическими погрешностями, представляет собой более сложную задачу, для каждого конкретного случая имеет идивидуальное решение.

Пример 3.

Проложен полигонометрический ход из n пунктов. Дирекционные углы и длины сторон хода имеют значения a₁ , a₂ ,... a_n и l₁, l₂ ,... l_n. Определить среднюю квадратическую погрешность координаты X конечного пункта хода, обусловленную погрешностью компарирования рулетки, если оно выполнялось в соответствии с требованиями “ Инструкции ...” [ ].

Решение

Компарирование рулетки выполнено с допустимой погрешностью 1 / 15000, установленой в [ ]. Следовательно, средняя квадратическая погрешность компарирования составила m_q =1 / 3000. Тогда для произвольной длины хода l_i истинную погрешность, обусловленную неточным компарированием, можно в среднем считать равной

Координата X конечного пункта хода определялась как функция измеренных длин

Погрешность m_q сохраняет свой знак и величину для каждой длины. Поэтому обсловленная ею погрешность координаты X должна определяться как суммарное влияние истинных погрешнотей всех длин из выражения

или

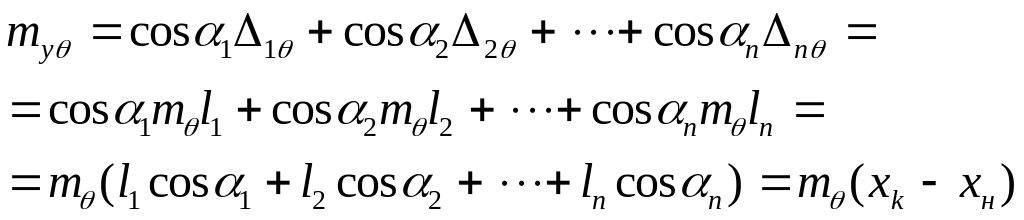
Как видим, имея вычисленный полигонометрический ход, нетрудно найти величину m_xq .