Формула сімпсона

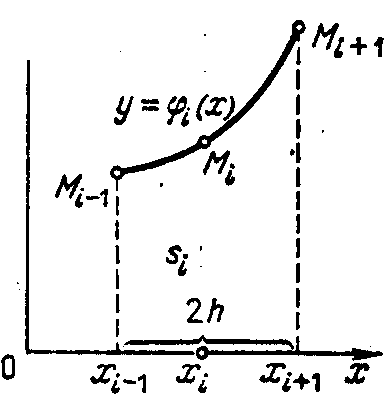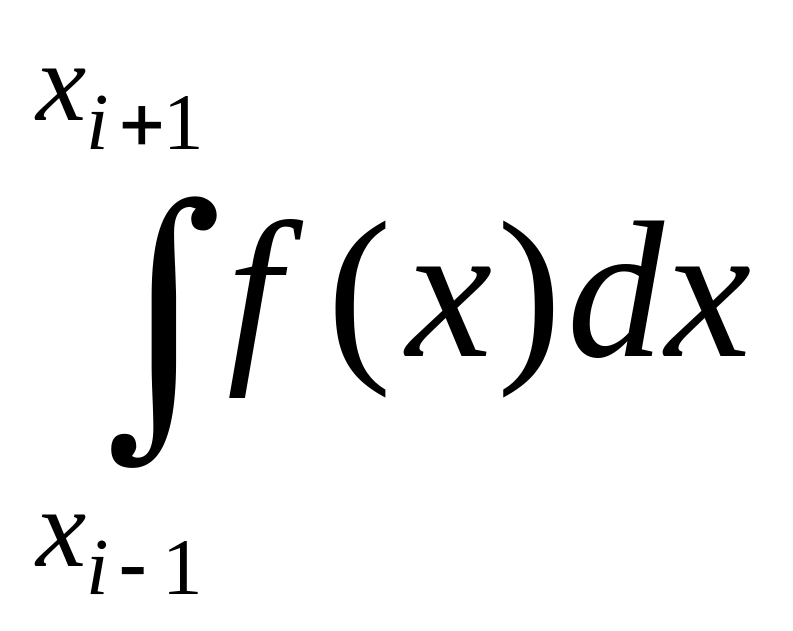Щ об побудувати триточкову квадратурну формулу з рівновіддаленими вузлами для обчислення наближеного значення , де f(х) — неперервна на [х_i-1;х_i+1] разом зі своїми похідними до четвертого порядку включно, можна використати інтерполяційний многочлен Лагранжа 2-го порядку, графік якого проходить через точки М_і-1(х_i-1; f(х_i-1)), М_і(х_i; f(xi)) іМ_і+1 (х_s+1;f (х_i+1 h)) і проінтегрувати його по x у межах від х_i-1 до х_i+1, де x_i+1-x_i=x_i-x_i-1=h.

Елементарна площа може бути обчислена за допомогою визначеного інтеграла:

Провівши такі обчислення для кожного елементарного відрізка {x_i-1,x_i+1}(і=1,2,…,n), підсумуєм отримані рівняння:

S=1/3*h(у_о+4y₁+2y₂+4y₃+2y₄+. . . . + 2у_n-2 + 4у_n-1, + у_n). (4.22)

Таким чином, формулу можна записати так:

+R(f) (4.23)

Це і є квадратурна формула Сімпсона, або формула парабол із залишковим членом. Вона точна для многочлена третього степеня, бо похідна четвертого порядку від такого многочлена дорівнює нулю.

Оцінка абсолютної похибки чисельного інтегрування за формулою Сімпсона:

│R(f)│ , (4.24)

де

M₄= , h= (b - а)/n

Приклад 3. Методом Сімпсона обчислити інтеграл

Всі обчислення будемо проводити в таблиці 5.

Таблиця 5

i	Xi	Yi=1/(1+xi2)
		i=0, i=10	Непарні i	Парні i
0	0	1
1	0,1		0,990
2	0,2			0,962
3	0,3		0,917
4	0,4			0,862
5	0,5		0,800
6	0,6			0,735
7	0,7		0,671
8	0,8			0,610
9	0.9		0,552
10	1	0,5

Знайдемо значення інтеграла по формулі (4.23):

Якщо порівняти результати обчислень інтеграла , отримані трьома різними методами тоді можна зробити наступний висновок:

Метод Сімпсона має більш високу точність; Для методу Сімпсона потрібно майже вдвічі менше табличних значень функції, оскільки для методу прямокутників потрібні додаткові дані в середніх крапках.

Порівняння і практична оцінка похибки квадратурних формул

Узагальнені формули трапецій і Сімпсона — це формули замкнутого типу. середніх прямокутників — відкритого типу, а лівих і правих прямокутників — напівзамкнутого і напіввідкритого типу. Як було уже зазначено, точне значення інтеграла визначають за формулами: лівих і правих прямокутників, якщо підінтегральна функція стала; середніх прямокутників і трапецій, якщо підінтегральна функція лінійна, і за формулою Сімпсона, якщо підінтегральною функцією є многочлен степеня, не вищого від третього.

Точність квадратурної формули характеризується порядком залишкового члена R(f) стосовно степеня кроку інтегрування h. З формул (4.13) , (4.14), (4.21) і (4.23) видно, що залишковий член R(f) квадратурних формул залежить від кроку інтегрування h і R(f) → 0 (h→0). Кажуть, що залишковий член R(f) має порядок р (р — натуральне число) відносно h, якщо існує скінченна границя

і записують це так: R(f) = O(h^p).

Отже, залишкові члени формул лівих і правих прямокутників відносно h мають перший порядок: R(f) =0(h), середніх прямокутників і трапецій — другий: R(f) = 0(h²), а Сімпсона — четвертий:R(f)=0(h⁴). Квадратурну формулу вважають тим точнішою, чим більший порядок її залишкового члена R(f). З розглянутих раніше квадратурних формул найточнішою є формула Сімпсона, а найменш точними — формули лівих і правих прямокутників. Точність формул середніх прямокутників і трапецій однакова.

Як було вище зазначено, іноді оцінити залишковий член квадратурної формули дуже важко або й неможливо, наприклад тоді, коли функцію задано графічно або таблично і аналітичний вираз її невідомий, або коли функцію задано складним аналітичним виразом і її похідні важко оцінити. Але якщо похідну певного порядку знайдено, то оцінити її за модулем на відрізку інтегрування завжди можна, побудувавши за допомогою ЕОМ таблицю значень похідної. Проте оцінити залишковий член R(f) квадратурної формули можна й тоді, коли не вдається оцінити зверху модуль похідної підінтегральної функції. Важливо лише знати порядок залишкового члена R(f) відносно кроку інтегрування h Для цього використовують метод подвійного перерахунку.

Нехай залишковий член деякої квадратурної формули має порядок р відносно кроку інтегрування А, тобто R(f) = 0(h^p), р Є N. Припустимо також, що похідна, яка входить до залишкового члена R(f) на відрізку інтегрування [a; b] змінюється мало, а тому наближено її можна вважати сталою. Тоді залишковий член R(f) набере вигляду

R(f)=Mh^p,

де М — деяка невідома стала.

Якщо відрізок [а; b] поділити на n і 2n рівні частини

h= ,

і обчислити за квадратурною формулою наближені значення I_n та I_2n, інтеграла, а відповідні їм залишкові члени позначити через Rn(f) і R_2n(f), то дістанемо дві рівності

I = In + Rn(f) = In + Mh^p,

I = I₂n + R_2n(f) = In + M(h/2)^p, (4.25)

Ці рівності можна розглядати як лінійну систему рівнянь відносно I і М. Виключивши з цієї системи I, знайдемо для М значення

M=

Підставивши це значення М у вираз для R_2n(f). дістанемо

R_2n(f)= (4.26)

Отже, залишковий член квадратурної формули пропорційний різниці двох наближених значень інтеграла, обчислених за цією ж квадратурною формулою з кроками h і h/2. Таку оцінку похибки квадратурної формули називають правилом Рунге. Якщо тепер (4.26) підставити у друге рівняння системи (4.25), то знайдемо уточнене значення інтеграла

I_n,2n=I_2n+ (4.27)

Обчислення наближеного значення інтеграла за формулою (4.27) називають екстраполяцією за Річардсоном. Якщо I_n≠ I_2n то уточнене значення I_n,2n ніколи не лежить між I_n, I_2n . Якщо I_2n> I_n то з формули (4.27) випливає, що I_n,2n > I_2n = max {I_n, I_2n} А якщо I_2n < I_n то I_n,2n < I_2n = min {I_n, I_2n} Отже, наближення I_n,2n визначають з наближень I_n та I_2n в результаті операції екстраполяції, тому й сам спосіб обчислення I_n,2n назвали екстраполяцією.

Для обчислення наближеного значення інтеграла з точністю є > 0 методом подвійного перерахунку треба:

1. Обчислити наближені значення інтеграла I_n та I_2n з кроком h та h/2

2. За формулою (4.26) обчислити наближене значення похибки R_2n(f) чисельного інтегрування.

3. Порівняти R_2n(f) з е. Якщо |R_2n(f) )| < ε, то за формулою (4.27) обчислити уточнене значення інтеграла I_n,2n і процес обчислень припинити. Якщо |R_2n(f) )|> ε, то, зберігши значення I_2n, відрізок [а; b] поділити на 4n рівних частин і обчислити R_2n(f) яке знову порівнюється з ε. Цей процес послідовного збільшення вдвічі числа вузлів квадратурної формули (зменшення вдвічі кроку інтегрування) продовжують доти, поки на певному кроці k не виконуватиметься нерівність

|R_2n(f) )| < ε.

45