Формула трапецій
Для обчислення наближеного значення I= підінтегральну функцію f, яка двічі неперервно диференційована на відрізку [хо; xo+h] (h > 0), замінюють інтерполяційним многочленом Лагранжа, що проходить через точки (хо; f(xo)) і (xo+h; f(xo+h));
f(x)=
,
(4.15)
Проіитегрувавши цю рівність по х у межах від хо до хо +h, дістанемо
=
(f(x0)+f(x0+h))+
Відкинувши в цій рівності залишковий член
R2(f)= . (4.16)
дістанемо квадратурну формулу
((f(x0)+f(x0+h))
(4.17)
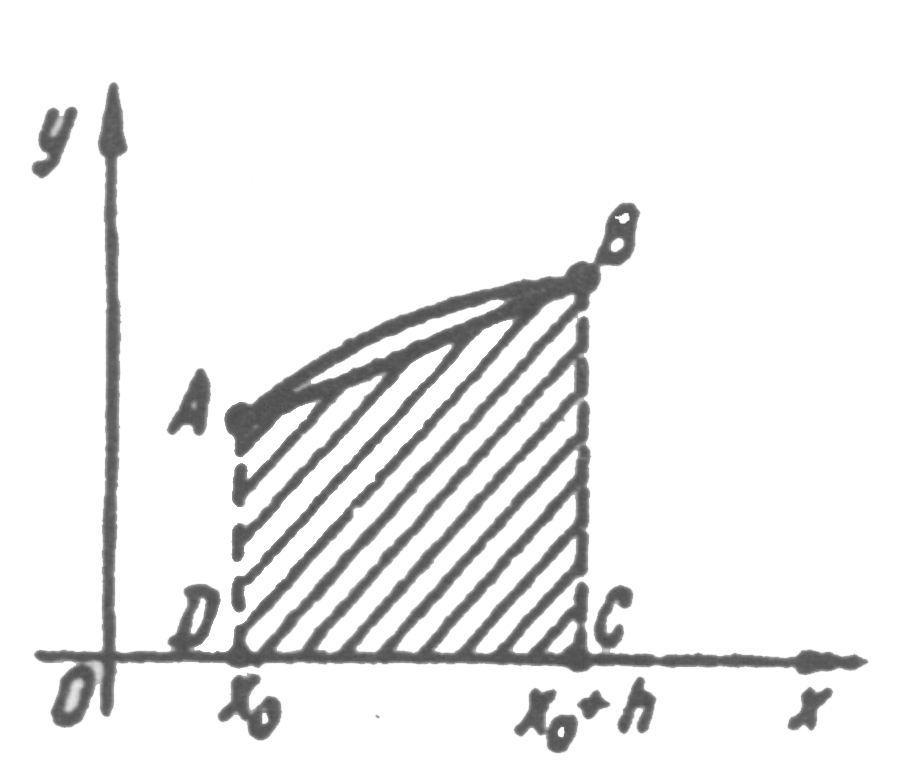
Якщо f(x) неперервна невідємна функція на відрізку [хо; хо +h], то наближену рівність (4.17) можна геометрично тлумачити так: за наближене значення криволінійної трапеції ABCD (рис. 4.3) береться площа заштрихованої трапеції ABCD. Тому формула дістала назву формули трапецій. Рис. 4.3
Якщо f"(x) неперервна на відрізку [хо;хо+h], то, застосувавши узагальнену теорему про середнє до інтеграла (4.16), знайдемо оцінка для абсолютної похибки чисельного інтегрування за формулою трапецій:
│R2(f)│
, (4.18)
де
M2= ,
Щоб обчислити наближене значення інтеграла , де f неперервна разом з похідними першого і другого порядків на [а; b], з достатньою точністю, відрізок [а; b] ділять на n рівних відрізків завдовжки h= (b - а)/n і до кожного з відрізків [хk, хk+1], (k =0,1,...,n-1) застосовують формулу трапецій із залишковим членом . Тоді відкинувши в цій рівності залишковий член R2(f) дістають квадратурну формулу
h= (b - а)/n (4.19)
яку називають узагальненою формулою трапецій.
Оскільки
f"(x)
неперервна на відрізку [а;
b],
то існує точка
[а;
b]
така,
що залишковий член узагальненої
формули
трапецій набирає остаточно вигляду
R2(f)=-
(b-a)f"(
),
[а;
b]
(4.20)
З (4.20) випливає, що узагальнена формула трапецій точна для лінійної функції, бо друга похідна від лінійної функції дорівнює нулю. Обчислити похибку чисельного інтегрування за узагальненою формулою трапецій не можна через те, що точка [а; b] формули (4.20) невідома. Але легко оцінити абсолютну похибку наближеного інтегрування за формулою (4.19)
│R2(f)│
, (4.21)
де
M2= , h= (b - а)/n
Примітка 1. Залишкові члени узагальнених формул середніх прямокутників і трапецій (див. (4.14) і (4.20)) мають протилежні знаки.
Отже, ці формули наближують інтеграл з недостачею і з надлишком, якщо f"(x) зберігає знак на [а; b]. Тому за наближене значення інтеграла I можна взяти півсуму цих двосторонніх наближень, тобто покласти I ≈ 0,5(Iср + Iтр) =І*. Тоді абсолютна похибка наближення І*
|І-І*| < |Іср-Ітр|.
Приклад 2. Методом трапецій обчислити інтеграл , з двома вірними десятковими знаками.
Для вибору кроку, з яким ми будемо обчислювати значеня підінтегральної функції, оцінимо величину поправочного члена.
Маємо:
f(х)
=
,
f’(x)=
, f’’(x)=-2*
і на відрізку 0≤x≤ 1 │f’’(x)│≤2│1-3x2│≤4.
За умовою задачі погрішність не повинна перевищувати 0,005. Маємо:
≤ 0.005
чи n2≥200/3
Для зручності обчислень бажано щоб крок виражався круглим числом. Тому візьмемо n=10, тоді крок h=0,1. Погрішність обчислень буде значно менше погрішності формули, якщо ординати будуть обчислені з точністю до трьох десяткових знаків.Бланк розрахунку тепер прийме вид в табл.4.
Таблиця 4
i |
Xi |
Xi2 |
1+xi2 |
Yi=1/(1+xi2) |
0 |
0 |
0 |
1 |
1 |
1 |
0,1 |
0,01 |
1,01 |
0,990 |
2 |
0,2 |
0,04 |
1,04 |
0,962 |
3 |
0,3 |
0,09 |
1,09 |
0,917 |
4 |
0,4 |
0,16 |
1,16 |
0,862 |
5 |
0,5 |
0,25 |
1,25 |
0,800 |
6 |
0,6 |
0,36 |
1,36 |
0,735 |
7 |
0,7 |
0,49 |
1,49 |
0,671 |
8 |
0,8 |
0,64 |
1,64 |
0,610 |
9 |
0.9 |
0,81 |
1,81
|
0,552 |
10 |
1 |
1 |
2 |
0,5 |
|
|
|
|
1,5 7,099
|
Звідси в силу формули (4.19) :
≈0,1 (0,5*1,5+7.099) =0,1*7,849 =0,7854981.
Для порівняння знайдемо значення заданого інтеграла по формулі Ньютона — Лейбница (з чотирма вірними десятковими знаками):
=arctagx
=arctgl—arctg 0= 0,7854.
Таким чином, у даному випадку формула трапецій дала результат більш точний. Погрішність тут дорівнює ΔI2=-0.00042 (близько 0.054%).