Формула прямокутників

Наближене значення інтеграла , де f неперервна на [х₀, х₀+h], можна знайти, якщо функцію f замінити інтерполяційним многочленом нульового степеня, тобто для всіх хє [х₀, х₀+h] покласти f(x) = f(c), де с є [х₀, х₀+h]. Тоді дістанемо наближену рівність

. (4.9)

Я кщо f(x) > 0 і неперервна на [х₀, х₀+h] , то наближену рівність (4.9) можна тлумачити геометричне так: за наближене значення площі криволінійної трапеції ABCD (рис. 4.1), обмеженої знизу віссю абсцис, зверху графіком функції f, а з боків прямими х =хо і х = хо+h, береться значення площі прямокутника MNCD. Тому формула (4.9) Рис. 4.1

дістала назву формули прямокутників.

Якщо с =x₀ або с =х_о + h, то (4.9) називають відповідно формулою лівих прямокутників

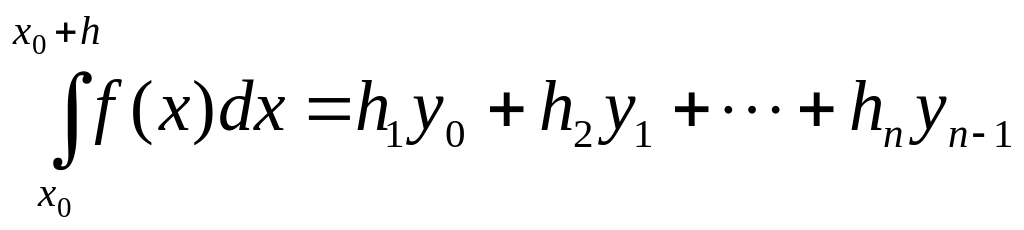(4.10)

Якщо с=х_о+h, то (4.9) називають формулою правих прямокутників

(4.11)

Якщо с =х_о+ h, то (4.9) називають відповідно формулою середніх прямокутників

h (4.12)

Знайдемо залишкові члени формул прямокутників, припустивши що підінтегральна функція f на [хо; xo+h] має неперервну похідну першого порядку (для випадку формул лівих і правих прямокутників) і неперервну похідну другого порядку (для випадку формули середніх прямокутників).

Похибки методу оцінюємо за формулами:

│R₁(f)│ , (4.13)

│R₂(f)│ , (4.14)

де

M₁= , M₂= ,

На рис 4.2 подано схему алгоритму чисельного інтегрування функцій за формулою середніх прямокутників. Відповідною програмою для інтеграла є програма 4.1.

Програма 4.1

10 PRINT " — Чисельне інтегрування методом"—

2 0 PRINT " —— середніх прямокутників"——

ЗО INPUT "Ввести нижню межу інтегрування А="; А

40 INPUT "Ввести верхню межу інтегрування В="; В

50 DEF FNY(X)=X*COS(X)

60 INPUT "Ввести число інтервалів N-";N

70 М=0; S=0: H=(B-A)/N: X=A-H/2

80 Х=Х+Н

90 F=FNY(X)

100 S=S+F: M=M+1

110 IFM<>N THEN80

120 I=S*H

130 PRINT "Для А="А; "В="В; "N="N

140 PRINT "Значення інтеграла І="І

150 GOTO 60

160 END

Приклад 1.Методом прямокутників обчислити інтеграл

I= .

Формула «лівих» прямокутників (4.10)

Тому що крок у нас постійний h=0.1, то по формулі «лівих» прямокутників (4.10) маєш:

I= 0.1(1+0.990+0.962+0.917+ +0.862+0.800+0.735+0.671+0.610+0.552)=0,8099

По формулі «правих» прямокутників одержимо наступний результат:

І = 0.1(0.990+0.962+0.917+0.862+0.800+0.735+

+0.671+0.610+0.552+0.5)=0.7599

Погрішність в обчисленні інтеграла складає ΔI₂=I₂-I=0.00021(близько 0.027%)

_{Для обчислення інтеграла по формулі «середніх» прямокутників треба спочатку обчислити значення функції в крапках X}i+1/2

Xi+1/2	0,05	0,15	0,25	0,35	0,45	0,55	0,65	0,75	0,85	0,95
Yi+1/2	0,9975	0,9779	0,9411	0,8908	0,8316	0,7677	0,7029	0,64	0,58055	0,5256

Тоді

= y_1/2h+y_3/2h+…+y_i-1/2h+…+y_n-1/2h=0.7856