2. Мерное метрическое пространство

Если в мерном векторном пространстве определить дополнительную операцию, называемую скалярным произведением векторов, то векторное пространство превращается в - мерное метрическое пространство. В этом случае говорят, что векторное пространство снабжено метрикой.

Определение 1. Любым двум векторам поставим в соответствие действительное число, называемое скалярным произведением векторов и , обозначаемое, как и удовлетворяющее следующим аксиомам:

1.

2.

3.

-6-

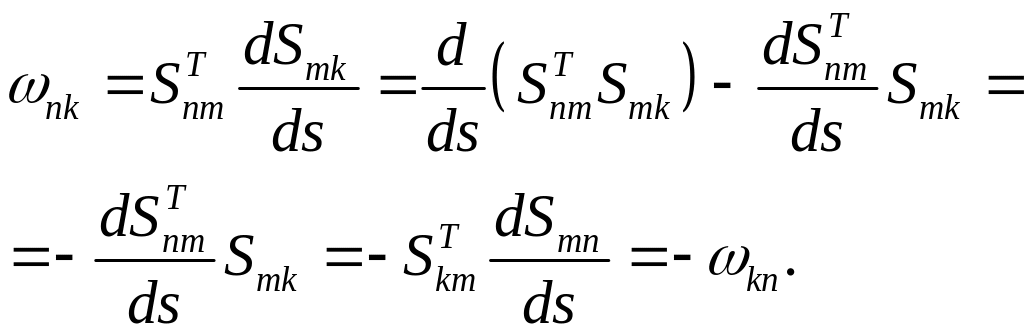
Антисимметричному тензору можно поставить во взаимнооднозначное соответствие вектор

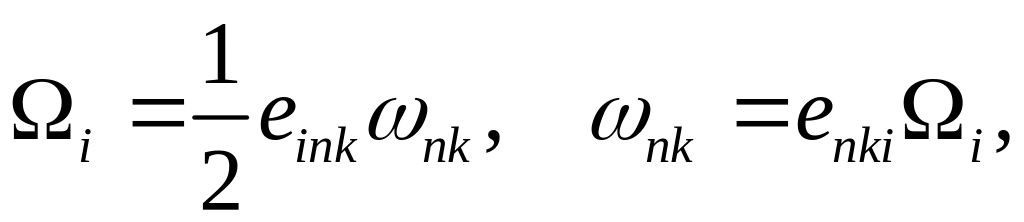(6.16a,b)

где - тензор (символ) Леви - Чивитта. Вектор , представленный своими компонентами (6.16) в декартовом базисе , называется вектором угловой скорости вращения ассоциированных базисов . Согласно (6.16a)

(6.17)

Подставляя (6.16 b) в (6.14) и учитывая (6.17), получаем формулу

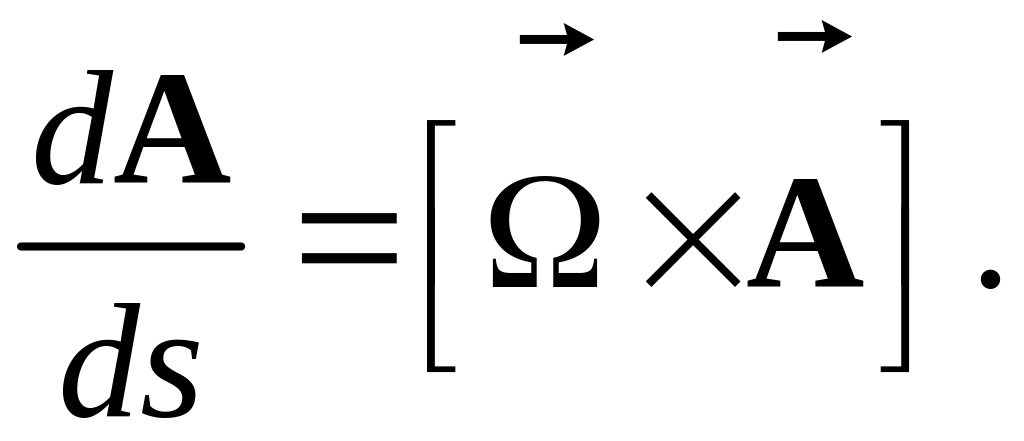(6.18)

Полученная формула определяет производную любого вектора в направлении кривой , обусловленную вращением ассоциированных базисов , а, следовательно, и вращением координатных

-43-

- длины ее дуги. Дифференцируя (6.9b) по вдоль кривой , получаем

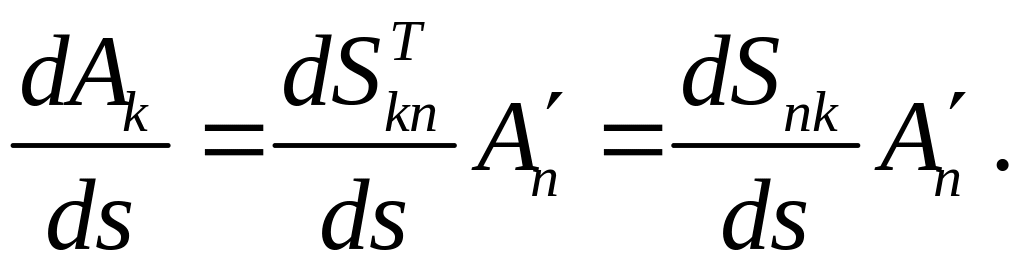(6.11)

Подставим значения из равенства (6.9 a) в (6.11), тогда

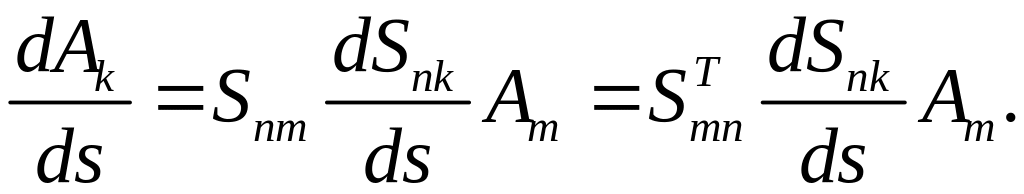(6.12)

Введем обозначение

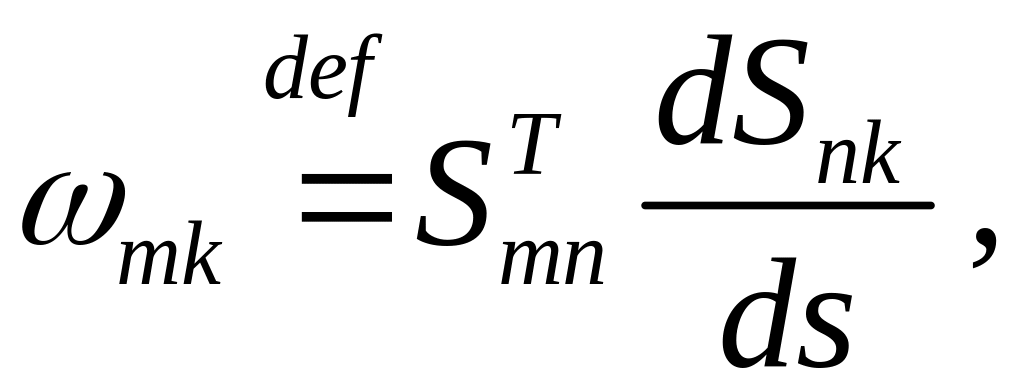(6.13)

и перепишем (6.12) в этих обозначениях

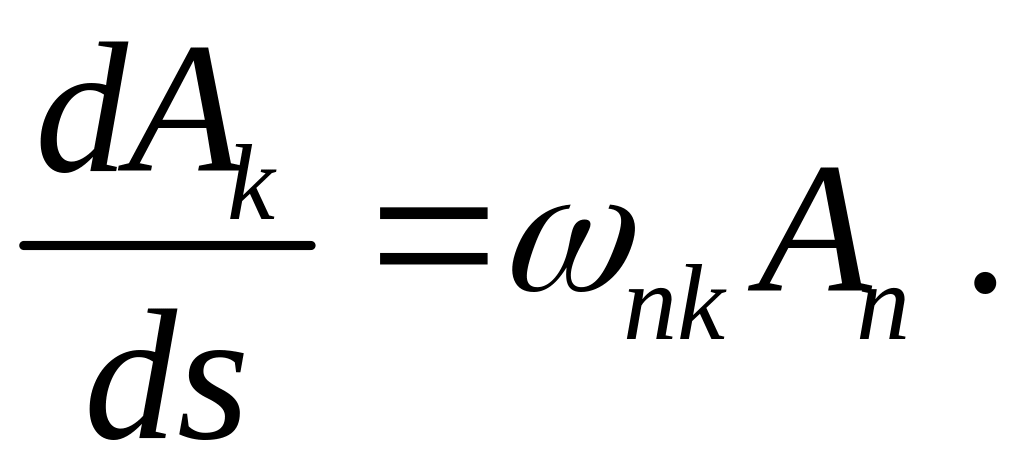(6.14)

Функции являются компонентами в декартовом базисе тензора 2-го ранга, называемого тензором вращения базисов . Покажем, что тензор вращения антисимметричен, т.е.

(6.15)

Воспользуемся для этого его определением (6.13) и ортогональностью (6.4) матрицы Имеем

-42-

Скалярное произведение в общем случае не обязано быть положительным числом. Если , то говорят, что вектор имеет “норму” или “модуль” равный В случае, когда , но не является нуль-вектором, говорят, что - изотропный вектор. Когда модуль вектора равен

Определение 2. Метрика пространства называется положительно определенной, если для любого , не являющегося нуль-вектором, и только для нуль-вектора . В противном случае, метрика пространства называется индефинитной.

Определение 3. Векторы и называются ортогональными, если

Следствие. Всякий изотропный вектор ортогонален себе.

Определение 4. Мерой угла между направлениями любых двух неизотропных векторов и является величина

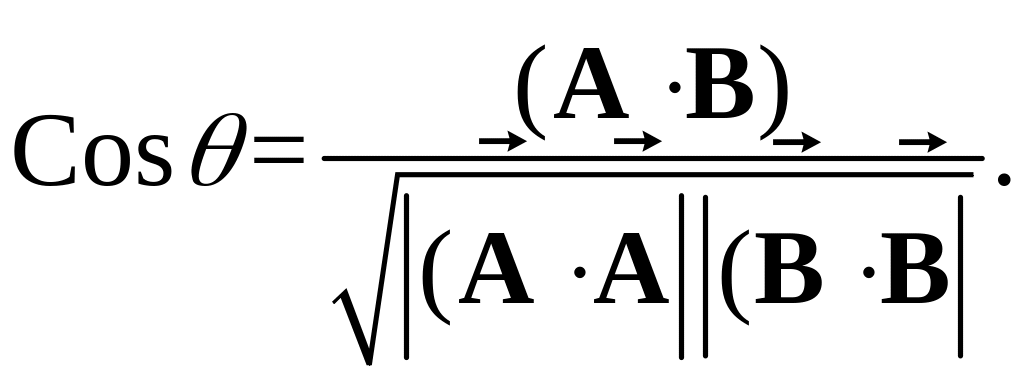(2.1)

Заметим, что в пространстве с индефинитной метрикой правая часть равенства (2.1) по модулю

может превышать единицу. Поэтому это равенство

-7-

следует понимать как формальное определение функции . В пространстве с положительно определенной метрикой правая часть (2.1) совпадает с традиционным определением тригонометрической функции .

Примеры метрических пространств,

используемых в физике

1.Трехмерное евклидово пространство с положительно

определенной метрикой. Классическая физика.

2. Четырехмерное пространство-время Минковского с

индефинитной метрикой. Специальная теория

относительности.

3. Четырехмерное риманово пространство-время с

индефинитной метрикой. Общая теория

относительности.

4. Пространство скоростей в специальной теории

относительности совпадает с трехмерным

пространством Лобачевского - Боияи с

положительно определенной метрикой.

Упражнение.

Показать, что в пространстве с положительно

определенной метрикой область изменения правой части выражения (2.1) совпадает с интервалом .