2 Решение задачи Коши для системы оду первого порядка и уравнений высших порядков

2.1. Система двух уравнений первого порядка. Рассмотрим алгоритмы Рунге-Кутта решения задачи Коши для систем ОДУ на примере системы двух уравнений:

Здесь штрихом обозначено дифференцирование по независимой переменной , и - начальные значения соответственно неизвестных функций и .

Методы Эйлера, описанные в подразделах 1.1. и 1.2., переносятся на случай системы (2.1) очевидным образом. Приведём формулы метода Эйлера, аналогичные формулам (1.3):

Модифицированный метод Эйлера для системы (2.1) даёт:

Формулы алгоритма Рунге-Кутта 4 порядка [5], которые обобщают формулы (1.8) для системы (2.1), запишем в виде:

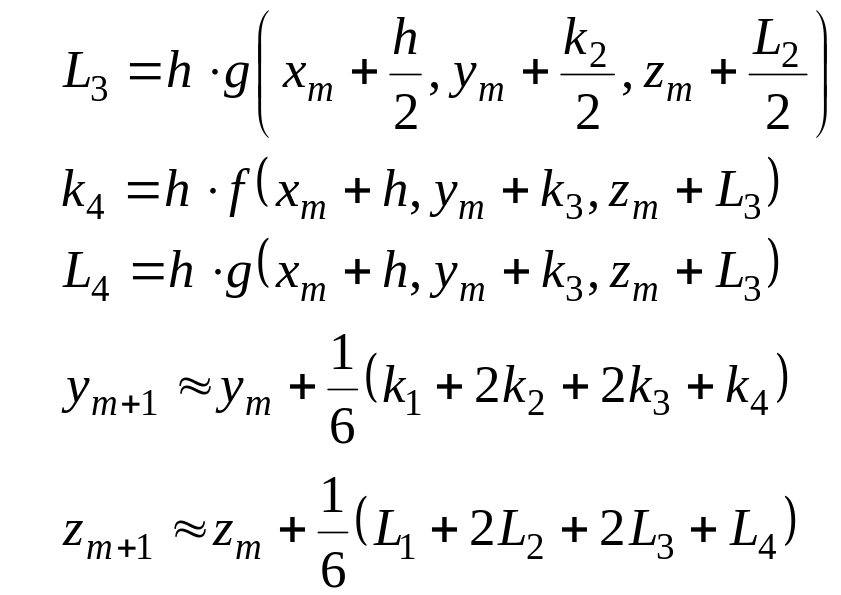
Наконец, приведём выражения метода прогноза и коррекции, обобщающие формулы (1.14), (1.15) и (1.18) для системы (2.1):

Уточним, что первая пара формул (2.5) отвечает за прогноз на текущем шаге, вторая пара – за коррекцию, а третья пара – за окончательные (уточнённые) значения неизвестных функций на этом шаге. Кроме того, к этой группе формул нужно добавить ещё две, позволяющие начать алгоритм – либо находясь в начале процесса, либо в случае, когда приходится менять его шаг.

2.3. Решение задачи о падении тел. В качестве примера реальной физической проблемы, которая моделируется системой ОДУ, изучим задачу о падении тел [4], причём будем рассматривать двумерные траектории. Введём систему координат xoy, ось oy направим вертикально вверх. Рассмотрим тело массой с начальной скоростью , направленной под углом к горизонту. На это тело (материальную точку) действуют сила тяжести и тормозящая сила , направленная в сторону, противоположную направлению скорости (здесь черта сверху обозначает векторную величину; ниже через и обозначим модуль соответствующего вектора). Уравнения движения тела на основании второго закона Ньютона можно записать в виде

Здесь принято, что тормозящая сила пропорциональна квадрату скорости движения тела; считается, что коэффициент зависит от свойств среды и геометрии тела; и - мгновенные координаты тела. Подставляя выражение для силы из (2.8) в (2.6), (2.7), учитывая равенства , и обозначение , уравнения (2.6) и (2.7) перепишем в виде

Систему уравнений (2.9), (2.10) дополним начальными условиями

Начальные значения для второй пары условий (2.11) вычисляются через указанные выше величины по формулам , .

Задачу (2.9)-(2.11) можно решать при помощи формул метода Рунге-Кутта. Но мы применим обобщение метода прогноза-коррекции. Для компактности записи введём обозначения

Используя обозначения (2.12), задачу Коши (2.9)-(2.11) перепишем в виде

Для вычисления значений неизвестных функций на первом шаге используем формулы модифицированного метода Эйлера:

Далее при вычислении значений неизвестных на следующих шагах используются собственно формулы прогноза и коррекции. Для значений прогноз даётся формулами

Эти выражения аналогичны формулам (1.14) и (2.5). Коррекция значений , , , производится по формулам, аналогичным (1.15):

На каждом шаге решения требуется, чтобы итерации для функций и и связанных с ними и проводились по очереди.

Отметим также, что окончательные значения неизвестных функций на каждом шаге следует вычислять аналогично (1.18) по формулам:

2.5. Решение задачи Коши для ОДУ высших порядков. Всякое ОДУ высокого порядка может быть (при помощи замен производных на новые неизвестные функции) приведено к системе ОДУ первого порядка, методы решения которой рассмотрены выше. Применим данный подход к задаче Коши для ОДУ 2 порядка (задачи Коши для ОДУ более высоких порядков обрабатываются аналогично):

Введём новую неизвестную функцию при помощи замены . Тогда задачу (2.17) можно переписать в следующем виде:

Запишем расчётные формулы методов Эйлера и Рунге-Кутта 4 порядка (т.е. соотношения (2.2), (2.3) и (2.4)) для системы (2.18). Метод Эйлера даёт:

Модифицированный метод Эйлера приводит к соотношениям:

После очевидных преобразований формулы метода Рунге-Кутта 4 порядка можно привести к виду:

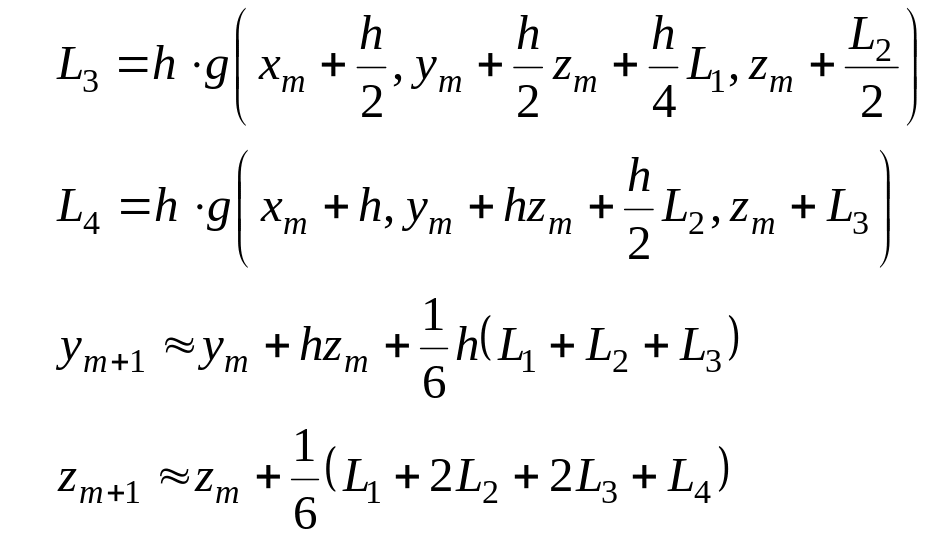
2.7. Решение задачи о колебаниях маятника. Данная задача моделируется следующей задачей Коши [6]:

Здесь - длина маятника; - неизвестная функция, относительно которой решается задача (2.17), – это угол между маятником и вертикальной осью; - ускорение силы тяжести; - коэффициент трения среды, в которой колеблется маятник; и - начальные значения соответствующих функций. Задача Коши (2.22) для ОДУ 2 порядка приводится к задаче Коши для системы двух ОДУ 1 порядка вида (2.18) при помощи следующих замен неизвестных, функций и производных:

Мы уже поднимали вопрос, каким образом при исследовании реальной задачи Коши без известного ответа можно убеждаться в том, что получаемое решение является верным. Указывались два пути: уменьшение шага разбиения отрезка интегрирования (при этом, даёт нам теория методов, погрешность на шаге должна убывать) и решение разными методами. Есть ещё один путь. Он состоит в следующем. Многие задачи имеют естественнонаучное происхождение. Поэтому в процессе решения такой задачи представляется полезным и важным выделить её характерный «физический» параметр и следить за его поведением. Если оно является ожидаемым, то можно надеяться на правильность получаемого решения. На практике полезно применять все три вышеназванных подхода.

В задаче о колебаниях маятника естественным физическим параметром является его полная энергия , которая вычисляется как сумма кинетической и потенциальной энергии [4]:

Здесь - масса груза. Следует вычислять полную энергию по формуле (2.23) на каждом шаге интегрирования задачи Коши и, в случае отсутствия трения среды ( ) , следить за тем, меняется или нет её значение. Если не меняется (точнее – «колеблется» около её начального значения), то вычислительный процесс является физически адекватным реальности.