П.3. Нерухомі точки дробово-лінійного відображення

Якщо ми маємо відображення ( ), то для цього відображення нескінченно віддалена точка є нерухомою ( ). Якщо , то, як ми знаємо, це відображення має ще одну нерухому точку − . Таким чином, подивившись на , можна сказати, що у випадку дві нерухомі точки зливаються в одну. В цьому випадку ми цю точку називатимемо подвійною нерухомою точкою. Нехай тепер , де ( ), . Тут зрозуміло, що нескінченно віддалена точка нерухомою не буде. Для з’ясування має чи ні таке відображення нерухомі точки розв’яжемо рівняння

, .

Дивлячись на розв’язок рівняння, робимо висновок, що якщо величина під коренем 0, то це рівняння матиме один подвійний корінь, який буде для нашого відображення подвійною нерухомою точкою. Якщо ж величина під коренем відмінна від 0, то це рівняння має два різні корені, кожен з яких і буде нерухомою точкою нашого відображення. Таким чином ми встановили

Кожне дробово-лінійне відображення з множини завжди має дві нерухомих точки, які в окремих випадках можуть зливатися в одну.

З тільки що одержаного випливає, що якщо деяке дробово-лінійного відображення має 3 нерухомих точки, то воно є тотожним.

Скористаємось цим для того, щоб відповісти на питання: „скільки пар відповідних точок треба мати, щоб однозначно задати дробово-лінійне відображення?” Нехай маємо точки , , . Треба знайти дробово-лінійне відображення , яке ці точки перевело б в точки , , .

, , .

Розглянемо відображення . Це відображення точки , , переведе в точки , , . Тепер розглянемо відображення . Очевидно відображення − це дробово-лінійне відображення, яке точки , , переводить самі в себе. Отже, відображення має 3 нерухомі точки. Тоді воно є тотожним. Отже, , . Звідси випливає, що дробово-лінійне відображення цілком визначається трьома парами відповідних точок.

Тепер виникає питання як, маючи ці відповідні точки, задати дробово-лінійне відображення. Нехай маємо три скінченні точки , , і теж три скінченні точки , , . Постараємось знайти дробово-лінійне відображення , яке перші 3 точки перевело б в точки , , . Побудуємо відображення , яке точки , , із - площини відобразить в точки 0, , 1 -площини. З того, що і маємо,

.

Скориставшись тим, що , одержимо

.

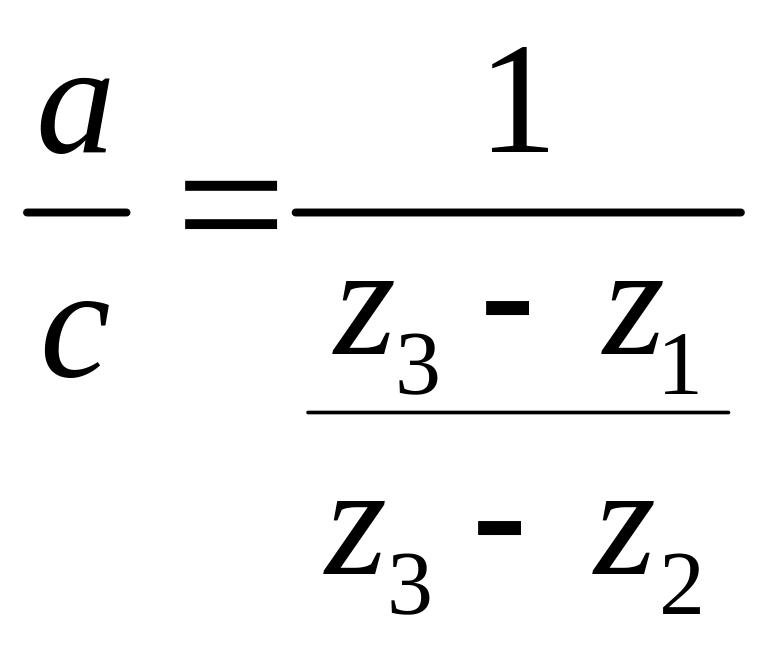Тому маємо,

.

Ми одержали відображення, яке точки , , із - площини відображає в точки 0, , 1 -площини. Позначимо через − відображення, яке переведе точки , , - площини в точки 0, , 1 -площини. Тоді знову одержимо,

.

Позначимо через − дробово-лінійне відображення, яке точки , , перевело б в точки , , . Розглянемо відображення . Це відображення , яке точки , , відображає в точки 0, , 1.

(1)

.

Остання формула вирішує, поставлену вище, задачу, бо відображення і відомі. Але, зручніше для запису цього відображення користуватися рівністю (1), в яку замість підставити . Будемо мати

або

. (*)

Це і є відображення, записане в неявному вигляді, яке скінченні точки , , - площини переводить в точки , , - площини.

З’ясуємо як виглядатиме наше відображення, якщо серед точок -х є нескінченно віддалена точка, наприклад . Будемо мати

.

Аналогічно і з випадками, коли серед чи є нескінченно віддалена точка. Зокрема, якщо і , то відображення матиме вигляд

.

Таким чином є таке мнемонічне правило:

якщо котрась із точок чи є нескінченно віддаленою точкою, то відповідні різниці, які містять ці точки, замінюються в одержаній вище формулі (*) на 1.

В математиці відоме складне відношення 4-х точок

.

З допомогою вище проведених викладок видно, що складне відношення 4-х точок є інваріантом при дробово-лінійному відображенні розширеної комплексної площини в себе.

О скільки коло в широкому розумінні однозначно задається 3-ма точками і дробово-лінійне відображення теж задається 3-ма парами відповідних точок, то очевидно має місце наступний факт: якщо в - площині є коло в широкому розумінні з 3-ма заданими на ньому точками , , і в - площині також є коло в широкому розумінні з 3-ма заданими на ньому точками , , , то існує єдине дробово-лінійне відображення, яке вказане коло - площини відобразить у вказане коло - площини так, що точки , , перейдуть при цьому відповідно в точки , , .

Нехай ми в - площині маємо коло в широкому розумінні і - одна із областей, на які розширену - площину ділить крива . І нехай , , − точки на кривій (рис. 11). Тоді − це буде та область, яка залишається зліва від спостерігача, який іде по колу від точки до точки через точку . А в - площині є теж коло в широкому розумінні і три точки на ньому , , - це та із двох областей розширеної -площини, на які ділить останню, яка залишається зліва від спостерігача, який іде з точки до точки через точку (рис. 12).

З найти дробово-лінійне відображення, яке , і . Побудуємо дробово-лінійне відображення (скориставшись попереднім пунктом), яке , , , . Це буде якесь дробово-лінійне відображення, яке крім того розширену комплексну - площину взаємно однозначно переведе на розширену -площину. Проведемо через точку дугу кола в широкому розумінні, яке ортогональне до кола і ця дуга починається в точці і закінчується в якійсь точці області . Тоді точку , яка є образом цієї точки , треба вибрати так, щоб відрізок кола в широкому розумінні (прямої) в нас був проведений таким чином, щоб поворот відбувався на цю ж величину і в цьому напрямі. Ясно, що така точка має бути області . Так видно, що довільна точка має образ, що лежить в області . Отже, відображається в . Насправді це відображення буде "на", бо якщо припустити, що в є точка , яка є образом якоїсь точки не з області , то легко прийдемо до суперечності з тим, що точу і точку не можна з'єднати дугою кола в широкому розумінні без перетину кривої .

З розв'язаної задачі випливає, що якщо потрібно відобразити якусь область -площини, яка одержується в результаті проведення кола в широкому розумінні, на якусь область -площини, яка отримується в результаті проведення в - площині кола в широкому розумінні, то потрібно на колі в широкому розумінні - площини вибрати три точки , , і подивитися з якої сторони від спостерігача знаходиться ця область, якщо рухатися з точки до точки через точку . Тоді на вказаному колі - площини точки , , слід вибирати так, що якщо ми будемо рухатися від точки до точки через точку , то щоб потрібна - область лежала з тієї ж сторони, що і в -площині.

Приклад. Відобразити верхню півплощину - площини ( ) на зовнішність одиничного кола в - площині так, щоб точки , , перейшли в точки , , .

Використавши формулу (*), будемо мати,

.

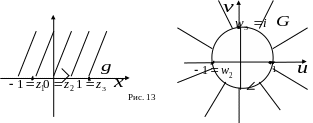
Оскільки область знаходиться зліва від спостерігача, який іде вздовж дійсної осі від точки до точки через точку і область теж знаходиться зліва від спостерігача, який рухається по колу від точки до точки через точку (рис. 13), то одержане відображення і розв’язує нашу задачу.

Нехай в - площині маємо деяку пряму і дві точки симетричні відносно цієї прямої, то зрозуміло, що пряма, яка проходить через ці дві точки і довільне коло з центром на даній прямій, що проходить через ці точки, будуть ортогональні до даної прямої. І навпаки, якщо є деяка пряма, що проходить через дві точки, яка перпендикулярна до прямої і всяке коло, що проходить через ці точки з центром на прямій , яке перпендикулярне до , то ці точки симетричні відносно прямої .

Подивимося, що буде робитися з цими точками при дробово-лінійному відображенні і , − точки симетричні відносно неї. Нехай ми маємо дробово-лінійне відображення , яке нехай спочатку пряму переведе в пряму -площини. Тоді це відображення всяке коло, яке проходить через і з центром на , переведе в коло, яке буде ортогональним до (в результаті конформності відображення) і пряму, яка пройде через і переведе в коло, яке буде ортогональним до .Точки і перейдуть в точки і . З вище сказаного випливає, що ці точки і будуть симетричними відносно (бо ми тільки що встановили, що всяке коло, яке проходить через точки і , ортогональне до і пряма, яка пройде через ці точки, теж ортогональна до ).

Зауважимо, що якщо задана пряма в -площині, наприклад , то маючи якусь точку можна одержати точку , яка симетрична відносно цієї прямої.

Ми встановили, що при дробово-лінійному відображенні зберігається симетрія відносно прямої. А оскільки дробово-лінійне відображення пряму може перевести в коло, то можна говорити у зв'язку з цим і про симетрію відносно кола і про збереження симетричних відносно кола точок при дробово-лінійному відображенні.