П.1 Логарифмічна функція і її властивості

Спробуємо одержати функцію, обернену до . Для цього потрібно розв'язати відносно рівняння. Вище ми такі рівняння розв'язували і з точністю до позначень отримали

.

Оскільки функція значення 0 не набирає, то щойно одержана функція визначена для . І оскільки вона є оберненою до експоненціальної (показникової), то логічно її називати логарифмічною функцією в комплексній області і позначати:

Число називають головним значенням логарифма.

Як і слід було чекати, бачимо, що логарифмічна функція в комплексній області є многозначною, зокрема нескінченнозначною, і значить при − це є нескінченна множина чисел.

З'ясуємо чи справедливі тут формули, аналогічні до формул з дійсного аналізу.

.

Аналогічно можна одержати

.

Останні дві формули означають рівність двох множин комплексних чисел. Забуваючи про це, можна допустити помилку. Розглянемо софізм, який належить Й. Бернуллі: для довільного . Справедливість цього твердження, здавалося б, випливає з таких рівностей:

1) ;

2) ;

3) ;

4) .

Але рівність 4) неправильна, бо

;

,

і жодне з чисел, взяте з множини , не збігається з жодним з чисел, взятим з множини . Помилка в цьому «доведенні» криється у незаконному переході від правильної рівності 2) до неправильної рівності 3). Справді, , оскільки множину чисел дістаємо додаванням будь-якого числа з множини до такого ж відмінного від нього числа з тієї ж множини. Отже,

,

Але справедливе таке включення

.

Приведений вище софізм Бернуллі показує, що оперувати з многозначними функціями складно і тому потрібно навчитися якось виділяти з цих функцій однозначні вітки. Нижче ми покажемо як це робиться для простіших многозначних функцій, а зараз знов повернемося до раніше введених нами тригонометричних функцій в комплексній області.

З означення тригонометричних функцій видно, що , . Враховуючи формули Ейлера, одержані вище, можна показати (врахувавши періодичність ), що обидві функції періодичні з періодом . Скориставшись формулами Ейлера і диференційованістю функції , легко одержати диференційовність і та справедливість рівностей:

,

.

Перевіримо чи справедлива для цих функцій відома зі школи формула додавання

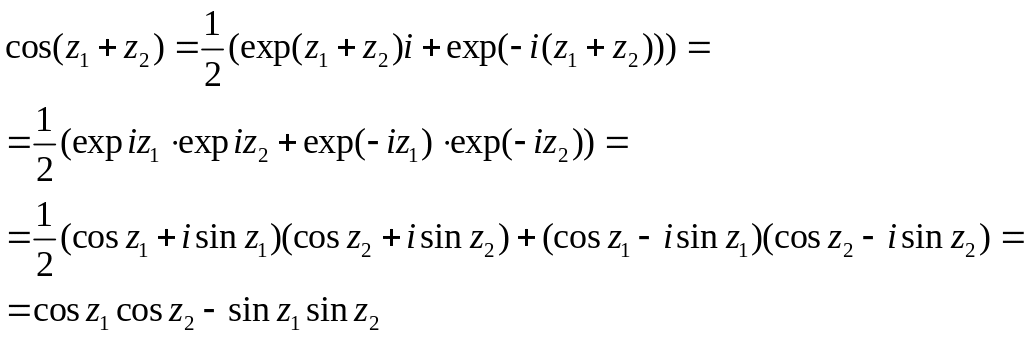
Міркуючи аналогічно легко одержимо інші формули додавання:

.

З цих формул одержуються формули зведення, подвійного кута і т. д., зокрема добре відома .

Оскільки і не зобов’язані тепер бути навіть дійсними числами (не те щоб додатними ), то з останньої рівності не можна зробити висновок про обмеженість синуса та косинуса в цій області. Для з’ясування останньої проблеми можна вибрати декілька шляхів і ми спочатку підемо таким: виділимо дійсну і уявну частину цих функцій і спробуємо оцінити модуль кожної з них. Для реалізації такого підходу нам потрібні гіперболічні функції, які можна ввести ще й так:

.

Обчисливши і , будемо мати,

,

.

Виділимо дійсну і уявну частини функцій і .

,

.

.

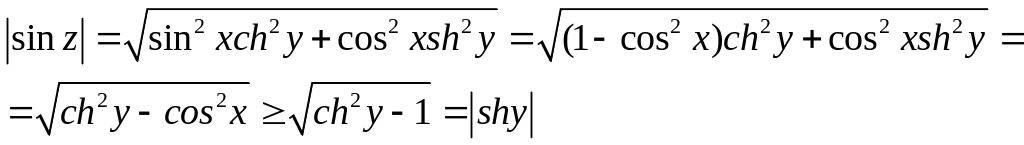Оскільки , то ми одержали наступні оцінки для :

.

А оскільки при крайні частини прямують до , то остання нерівність дозволяє стверджувати: синус в комплексній області є необмеженою функцією. Аналогічний результат має місце і для функції .

Що стосується відображень, що здійснюються цими функціями, то оскільки вони обидві виражаються через , а остання дає не взаємо однозначне відображення, то слід чекати, що ці відображення також не будуть взаємо однозначними. Для того, щоб мати більше уявлення про відображення, що здійснюються цими функціями можна зробити ту роботу, яку ми зробили з , почавши з відображення координатної сітки.