1.4. Встроенная подпрограмма excel “Поиск решения”.
EXCEL имеет специальную подпрограмму, позволяющую решать многие оптимизационные задачи, в том числе и задачи одномерной оптимизации.
Будем искать решение на том же рабочем листе. Выделим ячейку А63 для значений независимой переменной Х, а ячейку В63 - для значений целевой функции f(X). Занесем в ячейку В63 формулу =2*А63^2 + EXP(-A63).
В поле Установить целевую ячейку занесем адрес В63, с помощью переключателей в левой части диалога установим режим поиска минимального значения в этой ячейки. В поле Изменяя ячейки занесем адрес А63 и в списке Ограничения укажем дополнительные условия нахождения минимума c помощью кнопки Добавить. Для нашей задачи таких условий два: А630 и A631. Они указывают начальный интервал неопределенности, на котором целевая функция унимодальна.
Поиск решения начинается щелчком на кнопке Выполнить. Когда программа находит решение, открывается новый диалог Результаты поиска решений. Щелчком на кнопке ОК можно сохранить найденное решение.
1.5 Задания
Требуется решить задачу безусловной оптимизации функции
.
1).f(x)= 2*x3+12*x2+13*x+15.
2). f(x)= 2*x3-3*x2+4*x+9.
3). f(x)= x3-4*x2-4*x-5.
4). f(x)= 2*x4+3*x3+8*x2+6*x+5.
5). f(x)= 2*x4-3*x3+2*x2-15*x+14.
6). 15*x4-4*x3-6*x2-4*x-1.
7). f(x)= 2*x4-x3+3*x2-x+1.
8). f(x)= x4+3*x3-44*x2+15*x+25.
9). f(x)= 6*x4+25*x3+12*x2-25*x+6.
10). f(x)= x4-2*x3-11*x2+12*x+36.
11). f(x)= 100*x3+45*x2-12*x+2,5.
12). f(x)= 10*x3+20*x2-0,1*x-0,2 .
13). f(x)= x3+4,05*x2-0,03*x+0,02.
14). f(x)= x3+79,9*x2-1988*x-200.
15). f(x)= x3-4,6*x2-52*x-20.
16). f(x)= x3-0,5*x2-0,5*x.
17). f(x)= 200*x3+78*x2-41,2*x+0,42.
18). f(x)= 2*x3-0,6*x2+0,06*x-0,002.
19). f(x)= 0,5*x3-2,3*x2-26*x-10.
20). f(x)= -0,1*x3+0,405*x2+0,003*x-0,002.
21). f(x)= 2*x4+5*x3+3*x2-25*x+1.
22). f(x)= x4-3*x3-10*x2+2*x+6.
23). f(x)= 10*x3+5*x2-12*x+2.
24). f(x)= 7*x3+3*x2-5*x-2 .
25). f(x)= 2*x3+5*x2-3*x+5.
26). f(x)= x3+9*x2-8*x-20.
27). f(x)= 2*x3-6*x2-2*x-11.
28). f(x)= 3*x4-5*x3+2*x2-15*x+4.
29) ). f(x)= 5*x4-4*x3-7*x2-4*x-2.
30). f(x)=3*x4-2*x3+5*x2-x+1.
31). f(x)= x4+5*x3-4*x2+5*x+25.
32). f(x)= 6*x4+5*x3+10*x2-22*x+4.
33). f(x)= x4-4*x3-11*x2+15*x+16.
Многомерные задачи оптимизации.
2.1. Безусловная оптимизация: метод покоординатного спуска.
Это метод прямого поиска, в котором используются только значения целевой функции. Чтобы воспользоваться этим методом, необходимо иметь следующие исходные данные:
а) формулу целевой функции f(х1,х2, ... , хn),
б) Е - точность нахождения значений независимых переменных, при которых функция достигает минимума,
в) начальные приближения х10,х20 ... , хn0.
Зафиксируем все значения х-ов в виде начальных приближений, кроме первого. Тогда f(х1, х20 ... , хn0) - функция одной переменной х1. Решая задачу одномерной оптимизации, найдем минимум этой функции по координате х1 при фиксированных остальных координатах – хi1. В этом состоит первый шаг процесса оптимизации, заключающийся в спуске по координате x1.
Зафиксируем теперь все координаты, кроме x2. Снова решая одномерную задачу оптимизации, находим минимум функции по координате x2. Далее процедура повторяется до xn. На этом заканчивается первая итерация.
Таким образом, метод покоординатного спуска сводит многомерную задачу оптимизации к многократному решению одномерных задач по каждой независимой переменной.
После каждой итерации вычисляется
D = x1i+1 - x1i + x2i+1 - x2i + .... +xni+1 - xni
и если D<=E , то вычисления прекращаются и последний набор x-ов считается решением. В противном случае проводится следующая итерация.
Пример 2.1.
Число независимых переменных равняется двум. Ограничения отсутствуют. Требуется найти минимум функции
u = (x2-x12)2 + (1-x1)2
из начальной точки ( 0,5;0,5) c точностью 0,0001.
Проанализировав функцию, заметим, что она будет иметь минимум, равный нулю. Для чего и первое, и второе слагаемое тоже должны быть равны нулю. Откуда координаты точки минимума (1;1).
Решим эту задачу на EXCEL на новом рабочем листе.
Выделим столбец А под значения х1, столбец В - под значения х2, в столбец С будем заносить значения целевой функции и, наконец, в столбец D - значения погрешности D.
Занесем в ячейки А3 и В3 значения начальных приближений, равных 0,5 и в ячейку С3 формулу =(В3-А3^2)^2+(1-A3)^2. Скопируем эту формулу в блок ячеек С4:С17. На этом заканчивается подготовительный этап.
1 итерация.
1 шаг. Скопируем содержимое ячейки В3 в ячейку В4. Сделаем текущей ячейку С4. Процесс одномерной оптимизации для нахождения X1 выполним с помощью подпрограммы EXCEL Поиск решения.
В открывшемся диалоге в поле Установить целевую ячейку занесем адрес С4, а в поле Изменяя ячейки - адрес А4. Щелкнем по кнопке Выполнить и по кнопке ОК. В результате в ячейке А4 получим числовое значение, при котором целевая функция достигает минимального значения в ячейке С4 по координате х1.
2 шаг. Скопируем содержимое ячейки А4 в ячейку А5.
Текущая ячейка С5, меню Сервис- Поиск решения. В открывшемся диалоге в поле Установить целевую ячейку занесем адрес С5, а в поле Изменяя ячейки - адрес В5, Выполнить.
В результате в ячейке В5 получим числовое значение, при котором целевая функция достигает минимального значения в ячейке С5 по координате х2.
3 шаг. Занесем в ячейку D5 формулу =ABS(A3-A5)+ABS(B3-B5) для вычисления погрешности решения на первом шаге. На этом заканчивается первая итерация.
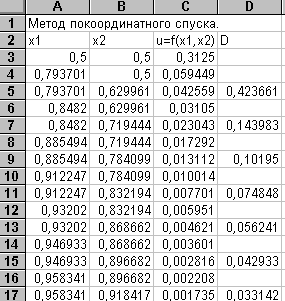
Вторая и все последующие итерации проводятся аналогично, но с учетом соответствующих адресов ячеек. Например, во второй итерации будут участвовать адреса ячеек в 6 и 7 строках. Результаты проведения первых семи итераций представлены в таблице. Как видно, значения целевой функции уменьшаются от шага к шагу, но метод сходится чрезвычайно медленно.
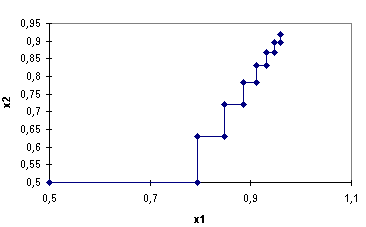
Можно построить диаграмму изменения на каждой итерации, выделив блок А2:В17 с помощью Мастера Диаграмм, выбрав тип диаграммы XY-точечная и формат 2. На диаграмме хорошо видны перпендикулярные ломаные линии движения от точки к точке параллельно одной из осей координат.
